0006 ALGO1001-跳马
使用广度优先搜索,首次抵达结束位置即为结果,或者走不到对应的点位,则输出 -1;
解题步骤
- 数据输入
- 数据初始化(棋盘初始化为无穷大,表示无法跳到此处)
- 将开始的位置置为 0,表示 0 步就可以到达这个位置,并将初始位置压入队列
- 遍历队列,取出当前位置
- 从当前位置可以到达的位置(8 个)判断是否降低了步数,若降低步数,则将当前位置数据压入队列
- 重复 4-5,直至队列为空或目标点位已抵达
- 判断步数,无法抵达置为 -1
马的位置判断:
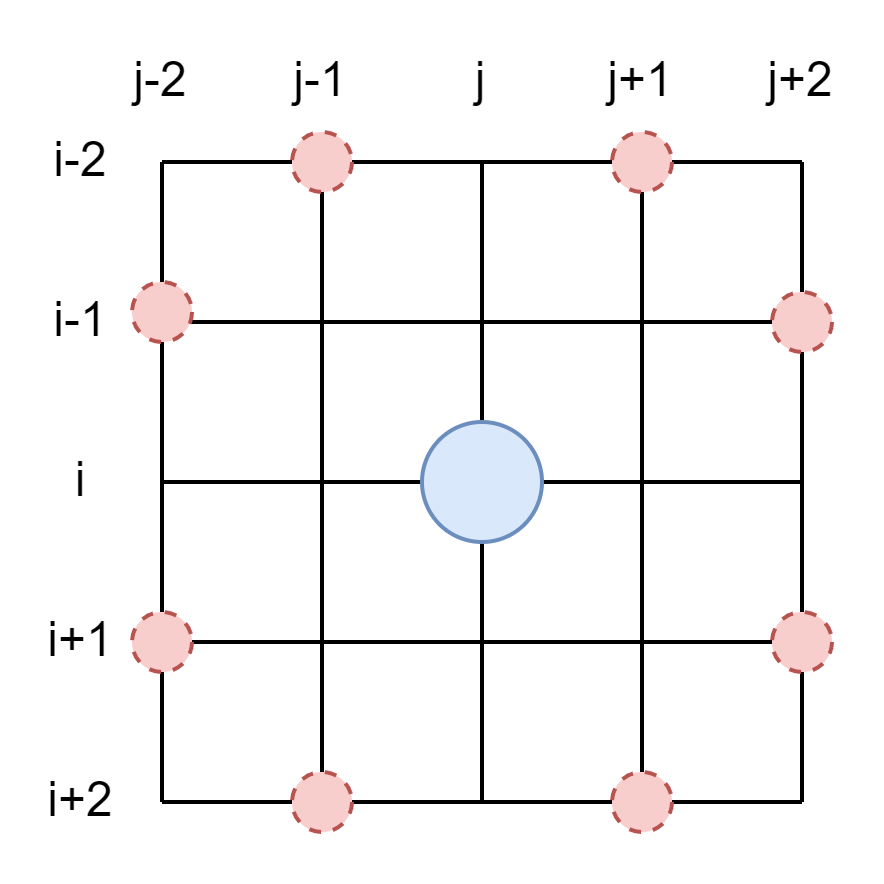
马有八面威风,就是八个可以走的点位
若马的初始点位在 \((i, j)\),则可以走的点位:
- \((i-2, j-1)\)
- \((i-1, j-2)\)
- \((i+1, j-2)\)
- \((i+2, j-1)\)
- \((i+2, j+1)\)
- \((i+1, j+2)\)
- \((i-1, j+2)\)
- \((i-2, j+1)\)
还要加上越界的判断
import java.util.Arrays;
import java.util.Scanner;
/**
* @author HuaWang135608
* @date 2023.03.15 10:26:13
* @description [试题 算法训练 跳马](http://lx.lanqiao.cn/problem.page?gpid=T2987)
*/
public class Main {
public static void main(String[] args) {
int[][] chessbord = new int[9][9];
int src_bi, src_bj, src_ei, src_ej;
// 数据输入
try (Scanner sc = new Scanner(System.in)) {
src_bi = sc.nextInt();
src_bj = sc.nextInt();
src_ei = sc.nextInt();
src_ej = sc.nextInt();
}
// 数据处理
// 初始化棋盘,代表跳到当前位置的步数是无穷大
for (int[] row : chessbord) {
Arrays.fill(row, Integer.MAX_VALUE);
}
// 以队列的形式压入下一步可以跳到的位置
int front = 0, rear = 0;
int[][] queue = new int[64][3];
queue[rear][0] = src_bi;
queue[rear][1] = src_bj;
chessbord[src_bi][src_bj] = queue[rear++][2] = 0;
// 队列为空或已抵达对应位置则退出循环(广度优先,首次抵达就是最优解)
while (front!=rear && chessbord[src_ei][src_ej]==Integer.MAX_VALUE) {
int i = queue[front][0];
int j = queue[front][1];
int v = queue[front++][2] + 1;
if (front == queue.length) {
front = 0;
}
// 若可以到达此处且步数少于已有的步数,则将当前位置压入队列,并更新步数
if (i>2 && j>1 && chessbord[i-2][j-1]>v) {
queue[rear][0] = i - 2;
queue[rear][1] = j - 1;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i - 2][j - 1] = v;
}
if (i>1 && j>2 && chessbord[i-1][j-2]>v) {
queue[rear][0] = i - 1;
queue[rear][1] = j - 2;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i - 1][j - 2] = v;
}
if (i<8 && j>2 && chessbord[i+1][j-2]>v) {
queue[rear][0] = i + 1;
queue[rear][1] = j - 2;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i + 1][j - 2] = v;
}
if (i<7 && j>1 && chessbord[i+2][j-1]>v) {
queue[rear][0] = i + 2;
queue[rear][1] = j - 1;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i + 2][j - 1] = v;
}
if (i<7 && j<8 && chessbord[i+2][j+1]>v) {
queue[rear][0] = i + 2;
queue[rear][1] = j + 1;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i + 2][j + 1] = v;
}
if (i<8 && j<7 && chessbord[i+1][j+2]>v) {
queue[rear][0] = i + 1;
queue[rear][1] = j + 2;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i + 1][j + 2] = v;
}
if (i>1 && j<7 && chessbord[i-1][j+2]>v) {
queue[rear][0] = i - 1;
queue[rear][1] = j + 2;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i - 1][j + 2] = v;
}
if (i>2 && j<8 && chessbord[i-2][j+1]>v) {
queue[rear][0] = i - 2;
queue[rear][1] = j + 1;
queue[rear++][2] = v;
if (rear == queue.length) {
rear = 0;
}
chessbord[i - 2][j + 1] = v;
}
}
int res = chessbord[src_ei][src_ej];
// 判断是否能跳到
if (res == Integer.MAX_VALUE) {
res = -1;
}
System.out.println(res);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号