0003 ALGO1005-蓝桥杯-数字游戏

试题 算法训练 数字游戏

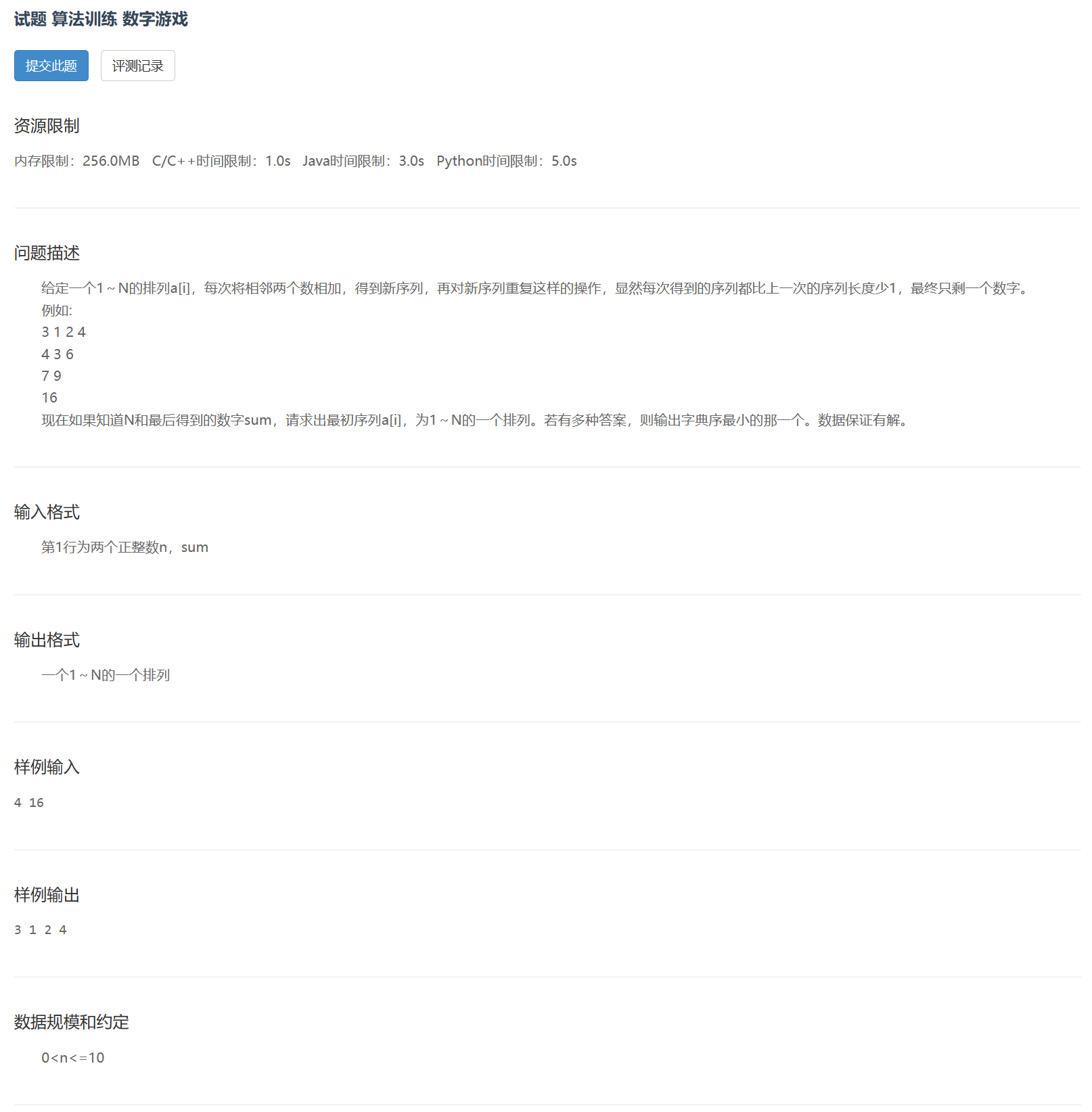
【分析】从 1~N 的排列得到和，相当于使用第 N 行的杨辉三角乘以这个序列
【思路】

1. 获取系数（求取杨辉三角的第 N 行）
2. 对 1~N 做全排列，与杨辉三角的第 N 行相乘，判断是否与给定的 sum 相同
   使用 dfs 深度优先搜索，获取 1~N 的全排列，且输出顺序要符合字典序（获取的第一个符合的排列就是需要的排列）

import java.util.Arrays;
import java.util.Scanner;
 
/**
 * @author HuaWang135608
 * @date 2023.03.11 14:58:38
 * @description [试题 算法训练 数字游戏](http://lx.lanqiao.cn/problem.page?gpid=T2995)
 */
 
public class A1005_NumberGame {
	
	public static void main(String[] args) {
		try (Scanner sc = new Scanner(System.in)) {
			// 数据输入
			int src_n = sc.nextInt(); // 输入数据量
			int src_sum = sc.nextInt(); // 输入求和结果
			int[] arrangement = new int[src_n]; // 排列数组
			
			// 数据处理
			// 初始化数据可用标记
			boolean[] available = new boolean[src_n];
			Arrays.fill(available, true);
			// 生成系数
			int[] coefficient = generateCoefficient(src_n);
			// 求结果
			boolean haveRes = dfs(arrangement, available, src_n, coefficient, src_sum);
			
			// 结果输出
			if (haveRes) {
				for (int val : arrangement) {
					System.out.print(val + " ");
				}
			}
			System.out.println();
		}
	}
	
	/**
	 * 获取系数，实际就是杨辉三角的最后一行
	 * @return
	 */
	public static int[] generateCoefficient(int length) {
		// 生成杨辉三角
		int[][] yangHuiTriangle = new int[length][];
		for (int i=0; i<yangHuiTriangle.length; ++i) {
			yangHuiTriangle[i] = new int[i + 1]; // 当前行数组
			yangHuiTriangle[i][0] = yangHuiTriangle[i][i] = 1; // 首尾均置 1
			// 第三行开始
			// 当前值（[i][j]）为左上（[i - 1][j - 1]）与上（[i - 1][j]）的和
			for (int j=1; j<i; ++j) {
				yangHuiTriangle[i][j] = yangHuiTriangle[i - 1][j - 1] 
						+ yangHuiTriangle[i - 1][j];
			}
		}
		// 获取杨辉三角最后一行，即为系数
		return yangHuiTriangle[length - 1];
	}
	
	/**
	 * 使用深度优先搜索，获取 1~N 的全排列
	 * 再使用全排列与系数做乘法，计算是否和 sum 一致
	 * @param arrangement 当前排列
	 * @param available 数据可用标记
	 * @param availableNum 剩余可用数据量
	 * @param coefficient 系数
	 * @param sum 系数和排列乘法要得到的结果
	 * @return 是否得到结果
	 */
	public static boolean dfs(int[] arrangement, boolean[] available
			, int availableNum, int[] coefficient, int sum) {
		if (availableNum == 0) { // 已无可用数据，查看当前排列是否为正确结果
			for (int i=0; i<arrangement.length; ++i) {
				sum -= arrangement[i]*coefficient[i];
			}
			return (sum == 0); // 若得到正确结果，返回 true
		}
		// 遍历可用数据，且未得到正确结果
		// 从小到大遍历，得到的排列结果符合字典序
		for (int i=0; i<available.length; ++i) {
			if (available[i]) {
				// 当前数据未使用，将 i+1 加入排列中 
				arrangement[arrangement.length - availableNum] = i + 1;
				available[i] = false; // 将当前数据设置为已被使用
				// 递归判断是否得到正确结果
				if (dfs(arrangement, available, availableNum - 1, coefficient, sum)) {
					return true;
				}
				available[i] = true; // 未得到正确结果，状态回溯
			}
		}
		return false;
	}
 
}

【参考】

1. 蓝桥杯（数字游戏）
2. java 蓝桥杯 数字游戏