做题记录

Posted on 2026-01-22 10:57 huangyuze114514 阅读(0) 评论(0) 收藏举报

2026年1月

P7410 [USACO21FEB] Just Green Enough S

我们可以发现，最小值恰好为 \(100\) = 最小值至少为 \(100\) - 最小值至少为 \(101\)。
因此，我们只需求出最小值大于等于 \(100\) 的子矩阵数和最小值大于等于 \(101\) 的子矩阵数然后相减就行了。

那么我们就可以建立一个 \(query\) 函数，用来查找最小值大于等于 \(cnt\) 的子矩阵数。
我们再建立两个数组：

\(b[i][j]\)：标记数组，若当前的数小于 \(cnt\)，那么标记为 \(1\)，否则为 \(0\)。
\(num[i][j]\)：关键数组，表示从第 \(i\) 行的第 \(j\) 列向左连续有多少个大于等于 \(cnt\) 的格子。

综上，我们就能写出求出 \(b\) 和 \(num\) 的代码：

for(int i=1;i<=n;i++){
	for(int j=1;j<=n;j++){
		if(a[i][j]<cnt){//小于cnt时，说明该点不符合标准
			b[i][j]=1;//标记
			num[i][j]=0;//重置
		}
		else{//否则符合答案
			b[i][j]=0;
			num[i][j]=num[i][j-1]+1;//因为该点符合标准，便可与前面符合的点连起来
		}
	}
}

这样，我们枚举每个点来当作子矩阵的右下角，那么此时 \(num\) 数组就会派上用场。若当前枚举到坐标为 \([i][j]\) 的数，那么只有 \(1\) 行的右下角坐标为 \([i][j]\) 的子矩阵数量就为 \(sum[i][j]\)。然后只有 \(2\) 行的子矩阵数就是 \(\min(num[i][j],num[i-1][j])\)，因为一行数的个数不能大于下面一行，否则就无法构成矩阵。
以此类推，直到第 \(1\) 行，就可以求出右下角坐标为 \([i][j]\) 的子矩阵数，即以下代码：

for(int i=1;i<=n;i++){
	for(int j=1;j<=n;j++){
		if(b[i][j])continue;//当前点小于cnt时，不符合答案
		long long minn=LLONG_MAX;
		for(int k=i;k>=1;k--){
			minn=min(minn,num[k][j]);//维护最小值
			ans+=minn;//更新答案
		}
	}
}

综上，就能写出代码：

#include<bits/stdc++.h>
using namespace std;
long long n,a[305][305],b[305][305],num[305][305];
long long query(long long cnt){
	long long ans=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(a[i][j]<cnt){//小于cnt时，说明该点不符合标准
				b[i][j]=1;//标记
				num[i][j]=0;//重置
			}
			else{//否则符合答案
				b[i][j]=0;
				num[i][j]=num[i][j-1]+1;//因为该点符合标准，便可与前面符合的点连起来
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(b[i][j])continue;//当前点小于cnt时，不符合答案
			long long minn=LLONG_MAX;
			for(int k=i;k>=1;k--){
				minn=min(minn,num[k][j]);//维护最小值
				ans+=minn;//更新答案
			}
		}
	}
	return ans;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cin>>a[i][j];
	long long ans1=query(100);
	long long ans2=query(101);
	cout<<ans1-ans2;
	return 0;
}

P7301 [USACO21JAN] Spaced Out S

我们发现，要么每一行的奶牛都是交替排列，要么每一列的奶牛都是交替排列。也就是在每一行（或列）中，奶牛要么全在奇数列（行），要么全在偶数列（行）。

因此，我们便只需要先计算每一行的 奇数列的数之和 和 偶数列的数之和 以及每一列的 奇数行的数之和 和 偶数行的数之和，再分类讨论，看看是行交替排列答案更大还是列交替排列答案更大。

#include<bits/stdc++.h>
using namespace std;
int n,x[1005][10],y[1005][10];
long long ans1,ans2;
int main(){
	cin>>n;
	int cnt;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin>>cnt;
      //计算每一行(列)的偶数和奇数列(行)之和
			x[i][j%2]+=cnt;
			y[j][i%2]+=cnt;
		}
	}
	for(int i=1;i<=n;i++){
		ans1+=max(x[i][1],x[i][0]);
		ans2+=max(y[i][1],y[i][0]);
	}
	cout<<max(ans1,ans2);
	return 0;
}

P7411 [USACO21FEB] Comfortable Cows S

如果一头牛在上下左右四个方向中，恰好在三个方向有牛和它相邻，就称它为“舒适的”。此时就需要在它唯一一个没有相邻牛的方向上添加一头牛，使它“不舒适”。
称在输入中的牛为主动添加的牛，称为了打破其他牛的“舒适”而添加的牛为被动添加的牛。

我们发现，当被动添加一头牛后，这头牛显然可能会引发更多的牛变为“舒适的”。因此，我们就要用到BFS。

我们不需要在每次加入一只主动添加的牛之后重新计算被动添加的牛，因为它们还是有用的。当加入的一只主动添加的牛与前面就加入的被动添加的牛重合，那么只需要把被动添加的牛的数量减 \(1\) 即可。

我们发现，被动添加的牛可能会越界。因此，我们在输入一组坐标后直接把 \(x\) 和 \(y\) 都加上 \(1000\) 就可以了。

#include<bits/stdc++.h>
using namespace std;
struct node{
	int x,y;
};
int n,cow[5005][5005],num[5005][5005],ans;
//cow的值为1代表主动添加的牛,2为被动添加的牛
//num为每头牛周围牛的数量
int dx[10]={0,1,0,-1,0};
int dy[10]={0,0,1,0,-1};
void update(int a,int b){//更新num数组
	for(int i=1;i<=4;i++){
		if(cow[a+dx[i]][b+dy[i]]){
			num[a][b]++;
			num[a+dx[i]][b+dy[i]]++;
		}
	}
}
void bfs(int a,int b){//更新被动添加的牛的数量，即ans;
	queue<node>q;
	for(int i=0;i<=4;i++)if(num[a+dx[i]][b+dy[i]]==3)q.push({a+dx[i],b+dy[i]});
	while(!q.empty()){
		node z=q.front();
		q.pop();
		int x=z.x,y=z.y;
		if(num[x][y]!=3)continue;
		int xx,yy;
		for(int i=1;i<=4;i++){
			if(!cow[x+dx[i]][y+dy[i]]){
				ans++;
				cow[x+dx[i]][y+dy[i]]=2;
				xx=x+dx[i];
				yy=y+dy[i];
				update(xx,yy);
				for(int j=0;j<=4;j++)if(num[xx+dx[j]][yy+dy[j]]==3)q.push({xx+dx[j],yy+dy[j]});
				break;
			}
		}
	}
}
int main(){
	cin>>n;
	int x,y;
	for(int i=1;i<=n;i++){
		cin>>x>>y;
		//加上1000防止越界
		x+=1000;
		y+=1000;
		if(cow[x][y]==2){//等于2时就代表这里已经有了被添加的牛
			cow[x][y]=1;//换为主动添加的牛
			ans--;//被添加的牛的数量-1
		}
		else{
			cow[x][y]=1;//标记
			update(x,y);//因为有新的牛加入,会对周围四个方向造成影响,所以要更新num数组
			bfs(x,y);//检查是否需要新的被动添加的牛
		}
		cout<<ans<<endl;
	}
	return 0;
}

P5019 [NOIP 2018 提高组] 铺设道路

算法：差分

题目给定一个数组，每次可对一个区间所有数减 \(1\)，问至少要多少步可以让数组的所有数都为 \(0\)。

我们发现，要快速地进行区间修改，我们可以使用差分。
因此，我们先构建一个差分数组。然后我们有知道，一次修改就是在差分数组上对一个数加上 \(1\)，再对一个数减去 \(1\)，目标是让差分数组变为一个全是 \(0\) 的数组。
综上，我们发现只需让差分数组中的正整数和负整数相互抵消，剩下来的数单独解决就可以了。又因为差分数组中不可能只存在负整数，所以剩下的数只能是正整数。
拿样例举例：

6   
4 3 2 5 3 5

我们先构建差分数组：

4 -1 -1 3 -2 2

我们发现，正整数总和为 \(9\)，负整数总和为 \(-4\)。相互抵消，便能够进行 \(4\) 次操作。那么抵消后便会剩下 \(5\)，那么再进行 \(5\) 此操作便能得到答案：\(9\)。

综上，我们很容易就能发现答案即为正整数之和。

#include<bits/stdc++.h>
using namespace std;
int n,a[100005],t[100005],ans;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		t[i]=a[i]-a[i-1];
		if(t[i]>0)ans+=t[i];
	}
	cout<<ans;
	return 0;
}

P4447 [AHOI2018初中组] 分组（需修改）

我们先统计每个实力值出现的次数，然后放到数轴上，然后我们就能得到：

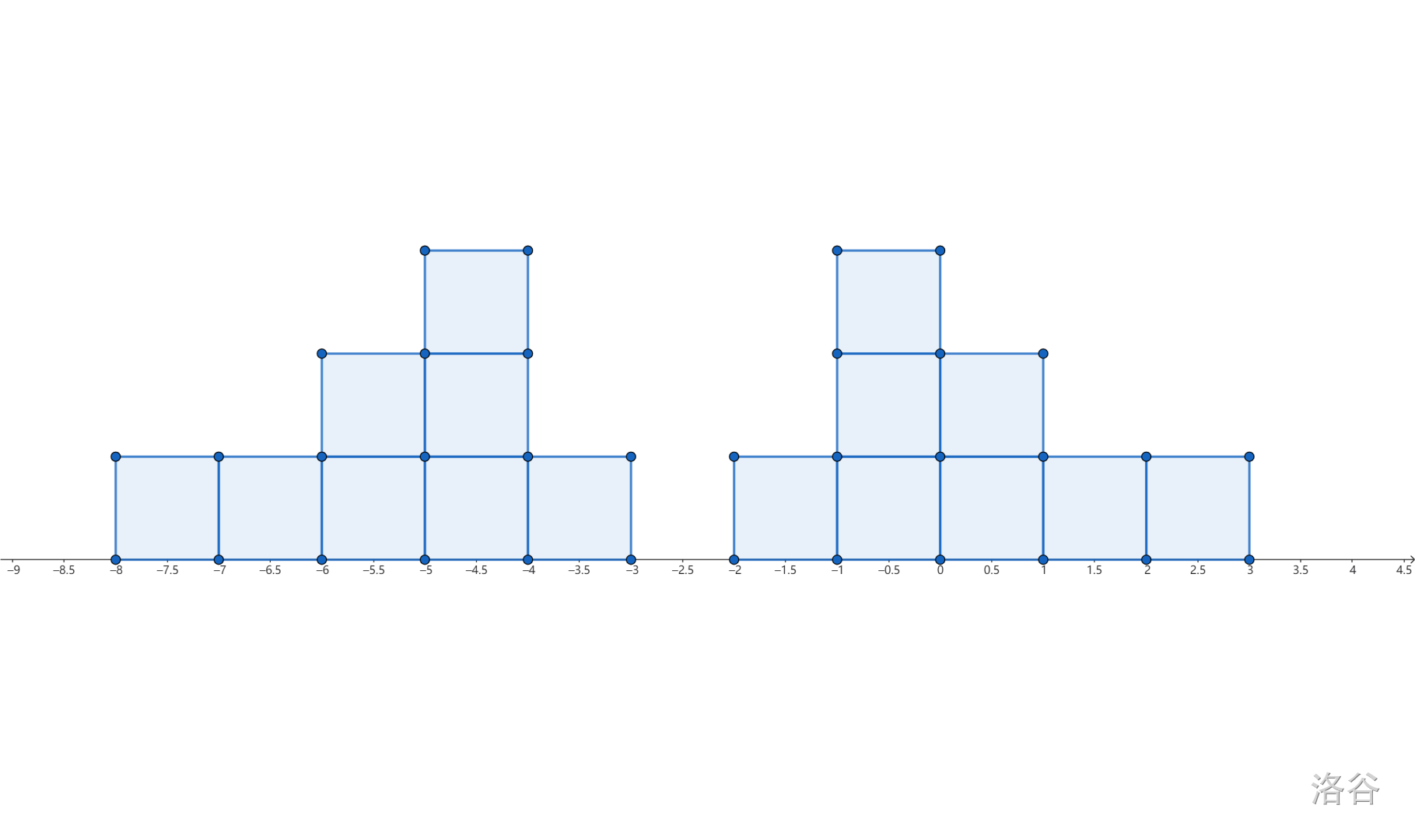
那么分组其实就是在数轴上画一条经过相连的方格的线。
那么正确的分组方式就是：

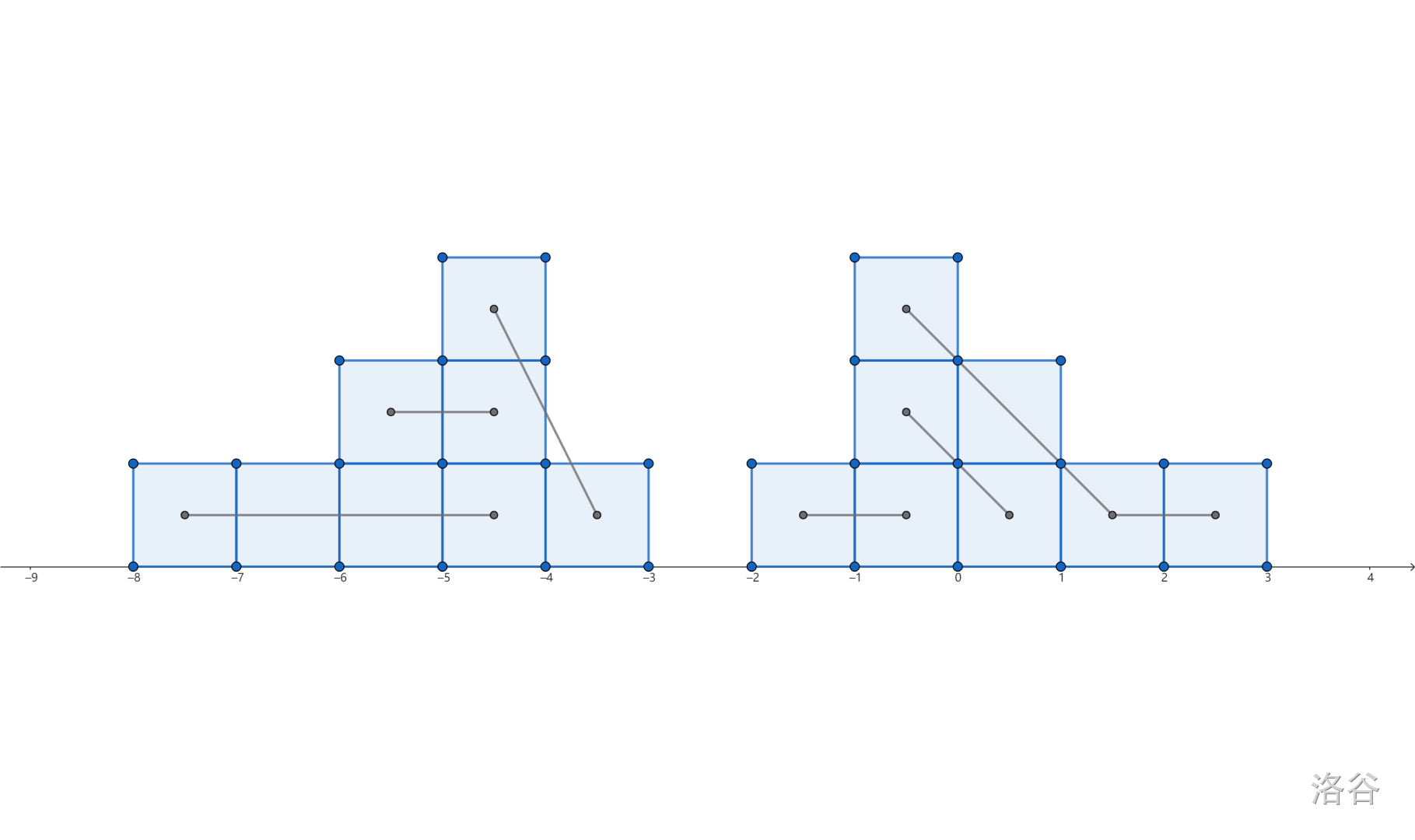
我们发现，如果每次分组都尽可能得往大的分，那么最小的组就会非常小。造成这种原因的是一些较高的方格数量很少，所以为了让这些较高的方块能分到的组人数较多，我们便可得出画线方案：
如果右边一列的高度不低于当前列，则连接右边一列最下方的方块。反之，停止画线。

显然，我们可以用 \(map\) 来实现代码。每次求一个组的长度，然后再求最小值即可。

#include<bits/stdc++.h>
using namespace std;
int n,ans=INT_MAX;
map<int,int>m;
int main(){
	int x;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		m[x]++;
	}
	while(!m.empty()){
		auto tag=m.begin();
		auto cnt=tag,next=tag;//cnt为当前遍历到的数,next为下一个数
		(*cnt).second--;//当前的数要被划入一个组,该数剩余的数量减1
		int len=1;//当前组的长度
		next++;
		//next不能越界,实力值跟cnt要相连,且next的值要大于等于cnt的值。因为cnt的值已经减1了,所以用>
		while(next!=m.end()&&(*cnt).first+1==(*next).first&&(*next).second>(*cnt).second){
			//当前next符合条件,入组
			len++;//长度++;
			cnt=next;//当前值往前进一位
			next++;//next往前进以为
			(*cnt).second--;//当前数减1
		}
		//去除已经为零的数,避免重复计算
		cnt=m.begin();//设为当前组的开头
		//因为一个组的实力值是递增的,所以如果当前组的开头不为0,那么后面的数也不会为0,就没必要遍历了;
		while(cnt!=m.end()&&(*cnt).second==0)m.erase(cnt++);
		ans=min(ans,len);//求值
	}
	cout<<ans;
	return 0;
}

P3842 [TJOI2007] 线段

纯DP

因为要把整个线段都走一遍，所以最优终点要么是线段最左端要么是线段最右端。
故我们设DP数组的定义为 \(f[i][j]\) 为走完第 \(i\) 行时总共走了多少步。其中当 \(j\) 为 \(0\) 时则代表做完后在最左端，当 \(j\) 为 \(1\) 时则代表做完后在最右端。
然后我们可以进行初始化。因为要求最小值，所以把数组所有数全设为 INT_MAX；因为每一行的答案要由上一行得来，所以我们要先初始化第 \(1\) 行。我们很容易发现，\(f[1][0]\) 即为 \(r[1]-1+len[1]\)，\(f[1][1]\) 即为 \(r[1]-1\)。

现在开始求状态转移方程。
对于第 \(i\) 行，一共有 \(4\) 种情况：

当终点在最左端：
- 由上一行最左端来：f[i][0]=f[i-1][0]+abs(r[i]-l[i-1])+len[i]+1
- 由上一行最右端来：f[i-1][1]+abs(r[i]-r[i-1])+len[i]+1
当终点在最右端：
- 由上一行最左端来：f[i][1]=f[i-1][0]+abs(l[i]-l[i-1])+len[i]+1
- 由上一行最右端来：f[i][1]=f[i-1][1]+abs(l[i]-r[i-1])+len[i]+1

#include<bits/stdc++.h>
using namespace std;
int n,f[20005][10],l[20005],r[20005],len[20005];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>l[i]>>r[i];
		len[i]=r[i]-l[i];
	}
	memset(f,INT_MAX,sizeof(f));
	f[1][0]=r[1]-1+len[1];
	f[1][1]=r[1]-1;
	for(int i=2;i<=n;i++){
		f[i][0]=min(f[i-1][0]+abs(r[i]-l[i-1]),f[i-1][1]+abs(r[i]-r[i-1]))+len[i]+1;
		f[i][1]=min(f[i-1][0]+abs(l[i]-l[i-1]),f[i-1][1]+abs(l[i]-r[i-1]))+len[i]+1;
	}
	cout<<min(f[n][1]+n-r[n],f[n][0]+n-l[n]);
	return 0;
}

刷新页面返回顶部