二分查找算法
简介
二分查找又称折半查找,用于在顺序存储结构(逻辑上相连的节点在物理存储上也相连,如数组)的并且关键字有序的线性表中查找关键字,是一种效率比较高的查找算法。
基本逻辑
假如需要查找的序列是一个非递减序列,首先把序列从中间分成两半。
1.如果查找的关键字跟序列中间关键字相同,说明查找到了,停止查找并返回位置。
2.如果要查找的关键字比序列中间关键字要小,说明需要查找的关键字在序列的前半部分,查找的序列的范围就变成前半部分;
3.如果要查找的关键字比序列中间关键字要大,说明需要查找的关键字在序列的后半部分,查找的序列的范围就变成后半部分;
4.再重新把上面的序列从中间分成两半,重复步骤1。直到要查找的序列的长度为0表示查找失败。
例子
待查找序列为0, 1, 7, 9, 11, 13, 18, 19
需要查找的关键字为18
首先把序列分成两半,前半部分为0, 1, 7, 9;后半部分为9, 11, 13, 18, 19。
1.由于待查找关键字18比中间的关键字9要大,说明查找的关键字在后半部分,即11, 13, 18, 19。
2.重新把序列分成两半,前半部分为11,13,后半部分为13, 18, 19。
3.由于待查找关键字18比中间的关键字13要大,说明查找的关键字在后半部分,即 18, 19。
4.重新把序列分成两半,前半部分为18,后半部分为18, 19。
5.由于待查找关键字18跟中间的关键字18相同,说明找到了,停止查找并返回位置6。
c/c++示例代码(递归和非递归实现)
1 #include <iostream> 2 using namespace std; 3 4 /************************************************************************/ 5 /* @brief 二分查找非递归实现 6 /* @param arr非递减数组 7 /* @param start数组查找范围起始下标 8 /* @param end数组查找范围结束下标 9 /* @param key需要查找的值 10 /* @return key在数组中的下标 -1表示没有查找到 11 /************************************************************************/ 12 int binarySearch(const int* arr, int start, int end, const int key) 13 { 14 int index = -1; 15 //如何传入的参数有问题,直接返回-1,查找失败 16 if (arr == nullptr || start < 0 || end < start) 17 { 18 return index; 19 } 20 21 while (end >= start) 22 { 23 int middle = (end - start) / 2 + start; 24 //查找到 25 if (arr[middle] == key) 26 { 27 index = middle; 28 break; 29 } 30 //查找的值比中间的值小,说明在前半部分 31 else if (arr[middle] > key) 32 { 33 end = middle - 1; 34 } 35 //查找的值比中间的值大,说明在后半部分 36 else 37 { 38 start = middle + 1; 39 } 40 } 41 return index; 42 } 43 44 /************************************************************************/ 45 /* @brief 二分查找递归实现 46 /* @param arr非递减数组 47 /* @param start数组查找范围起始下标 48 /* @param end数组查找范围结束下标 49 /* @param key需要查找的值 50 /* @return key在数组中的下标 -1表示没有查找到 51 /************************************************************************/ 52 int binarySearchR(const int* arr, int start, int end, const int key) 53 { 54 int index = -1; 55 //如何传入的参数有问题,直接返回-1,查找失败 56 if (arr == nullptr || start < 0 || end < start) 57 { 58 return index; 59 } 60 61 int middle = (end-start) / 2 + start; 62 //查找到 63 if (arr[middle] == key) 64 { 65 index = middle; 66 } 67 //查找的值比中间的值小,说明在前半部分 68 else if (arr[middle] > key) 69 { 70 return binarySearchR(arr, start, middle - 1, key); 71 } 72 //查找的值比中间的值大,说明在后半部分 73 else 74 { 75 return binarySearchR(arr, middle + 1, end, key); 76 } 77 78 return index; 79 } 80 81 int main() 82 { 83 int arr[8] = { 0, 1, 7, 9, 11, 13, 18, 19 }; 84 85 cout << "原始数据:" << endl; 86 87 for (int i = 0; i < sizeof(arr) / sizeof(int); ++i) 88 { 89 cout << arr[i] << " "; 90 } 91 92 int key = 18; 93 94 cout << endl << "查询结果:" << endl; 95 96 int index = binarySearch(arr, 0, 7, key); 97 98 cout << "非递归查找" << key << ":" << index << endl; 99 100 index = binarySearchR(arr, 0, 7, key); 101 102 cout << "递归查找" << key << ":" << index << endl; 103 104 return 0; 105 }
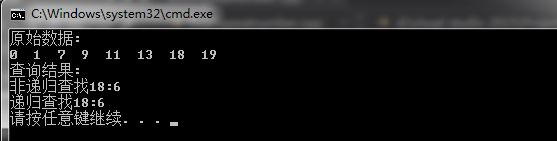
测试结果




 浙公网安备 33010602011771号
浙公网安备 33010602011771号