感知机——如何判断一个人的性别
1. 引子
目标:运用感知机,教会机器人通过外观去判断一个人的性别。
2. 数据
2.1 文字数据
| 头发(长发、短发、光头) | 衣服(长裤、裙子) | 性别(男、女) | |
| 路人1 | 长发 | 裙子 | 女 |
| 路人2 | 短发 | 长裤 | 男 |
| 路人3 | 光头 | 长裤 | 男 |
| 路人4 | 长发 | 长裤 | 女 |
| 路人5 | 短发 | 裙子 | 女 |
| 路人6 | 长发 | 裙子 | 女 |
| 路人7 | 长发 | 裙子 | 女 |
| 路人8 | 短发 | 长裤 | 男 |
|
路人9 |
短发 | 长裤 |
男 |
| 路人10 | 短发 | 长裤 | 男 |
2.2 数字数据
| x1 | x2 | label | |
| x1 | 1 | 1 | 1 |
| x2 | 0.5 | 0 | -1 |
| x3 | 0 | 0 | -1 |
| x4 | 1 | 0 | 1 |
| x5 | 0.5 | 1 | 1 |
| x6 | 1 | 1 | 1 |
| x7 | 1 | 1 | 1 |
| x8 | 0.5 | 0 | -1 |
|
x9 |
0.5 | 0 |
-1 |
| x10 | 0.5 | 0 | -1 |
3. 模型
$$f(x)=sign(w*x+b)$$
4. 策略
在模型空间中,选取使得$L(w,b)=-∑y_i(w*x_i+b)$最小的模型参数$w,b$,其中$x_i、y_i$属于误分类点,误分类:$y_i*(w*x_i+b)\le0$
5. 算法
5.1 SGD随机梯度下降法
($w_1=w_0+\eta*x_i*y_i,b_1=b_0+\eta*y_i,$假设$\eta=1$)
| 迭代次数 | 误分类点 | w | b | w*x+b |
| 0 | - | (0,0) | 0 | 0 |
| 1 | x1(1,1,1) | (1,1) | 1 | x1+x2+1=0 |
| 2 | x2(0.5,0,-1) | (0.5,1) | 0 | 0.5x1+x2=0 |
| 3 | x3(0,0,-1) | (0.5,1) | -1 | 0.5x1+x2-1=0 |
| 4 | x4(1,0,1) | (1.5,1) | 0 | 1.5x1+x2=0 |
| 5 | x8(0.5,0,-1) | (1,1) | -1 | x1+x2-1=0 |
| 6 | x4(1,0,1) | (2,1) | 0 | 2x1+x2=0 |
| 7 | x8(0.5,0,-1) | (1.5,1) | -1 | 1.5x1+x2-1=0 |
分离超平面:$1.5x^1+x^2-1=0$,将样本点完全正确的划分到两侧。
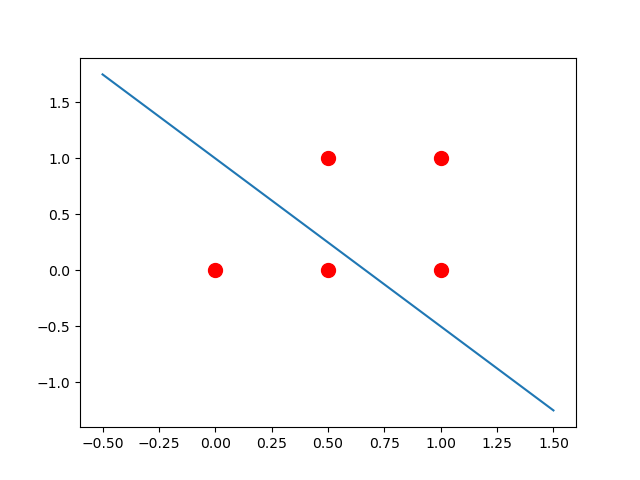
最优模型: $f(x)=sign(1.5x^1+x^2-1)$
5.2 BGD批量梯度下降法
($w_1=w_0+\eta*∑x_i*y_i,b_1=b_0+\eta*∑y_i$,假设$\eta=1$)(其中$x_i、y_i$属于误分类点)
| 迭代次数 | 误分类点 | w | b | w*x+b |
| 0 | - | (0,0) | 0 | 0 |
| 1 | x1:10 | (2.5,4) | 0 | 2.5x1+4x2=0 |
| 2 | x2,3,8,9,10 | (0.5,4) | -5 | 0.5x1+4x2-5=0 |
| 3 | x1,4,5,6,7 | (5,8) | 0 | 5x1+8x2=0 |
| 4 | x2,3,8,9,10 | (3,8) | -5 | 3x1+8x2-5=0 |
| 5 | x4 | (4,8) | -4 | 4x1+8x2-4=0 |
| 6 | x4 | (5,8) | -3 | 5x1+8x2-3=0 |
分离超平面:$5x^1+8x^2-3=0$,也将样本点完全正确的划分到两侧。
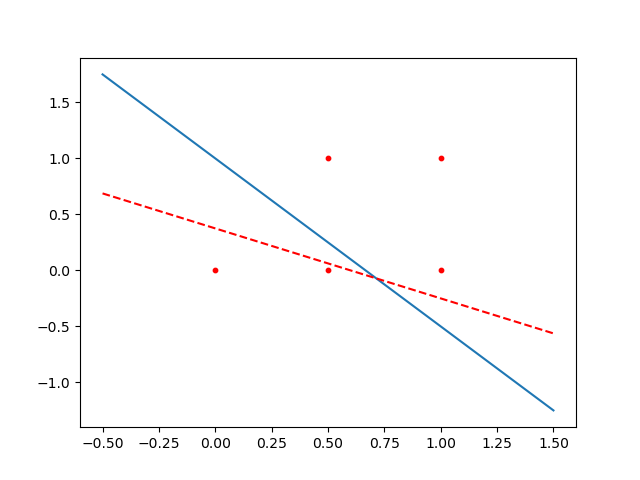
最优模型:$f(x)=sign(5x^1+8x^2-3)$
5.3 MBGD小批量梯度下降法
($w_1=w_0+\eta*∑x_i*y_i,b_1=b_0+\eta*∑y_i$,假设$\eta=1$)(其中$x_i、y_i$属于误分类点)(求和个数有限制,假设$batch=2$)
| 迭代次数 | 误分类点 | w | b | w*x+b |
| 0 | - | (0,0) | 0 | 0 |
| 1 | x1,2 | (1.5,1) | 0 | 1.5x1+x2=0 |
| 2 | x3,8 | (1,1) | -2 | x1+x2-2=0 |
| 3 | x1,4 | (3,2) | 0 | 3x1+2x2=0 |
| 4 | x8,9 | (2,2) | -2 | 2x1+2x2-2=0 |
| 5 | x4 | (3,2) | -1 | 3x1+2x2-1=0 |
| 6 | x2 | (2.5,2) | -2 | 2.5x1+2x2-2=0 |
分离超平面:$2.5x^1+2x^2-2=0$,将样本点完全正确的划分到两侧。
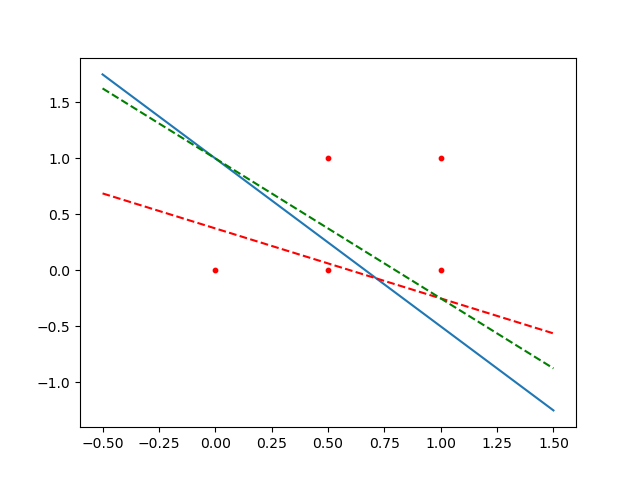
最优模型:$f(x)=sign(2.5x^1+2x^2-2)$
6. 预测
6.1 常规输入
以SGD算法得到的最优模型$f(x)=sign(1.5x^1+x^2-1)$为例,在预测时,输入(长发,裙子)的组合,即输入$(1,1)$,则输出$f(x)=sign(1.5*1+1*1-1)=sign(1.5)=1$,即判断此人的性别为女。以此类推输入$(1,0)$,输出$1$,即长发长裤的人的性别被判断为女。输入$(0.5,1)$,输出$1$,即短发裙子的人的性别被判断为女。输入$(0.5,0)$,则输出为$-1$,即短发长裤的人的性别被判断为男。输入$(0,0)$,则输出$-1$,即光头长裤的人的性别被判断为男。
6.2 特殊输入
样本数据中没有(光头,裙子)的组合,若预测时当输入为(光头,裙子)时,SGD算法得到的最优模型$f(x)=sign(1.5x^1+x^2-1)$,输出为$sign(0)=1$,判断为女生。BGD算法得到的最优模型$f(x)=sign(5x^1+8x^2-3)$,判断为女生。MBGD算法得到的最优模型$f(x)=sign(2.5x^1+2x^2-2)$,则输出为$sign(0)=1$,判断为女生。而实际是个大汉………………
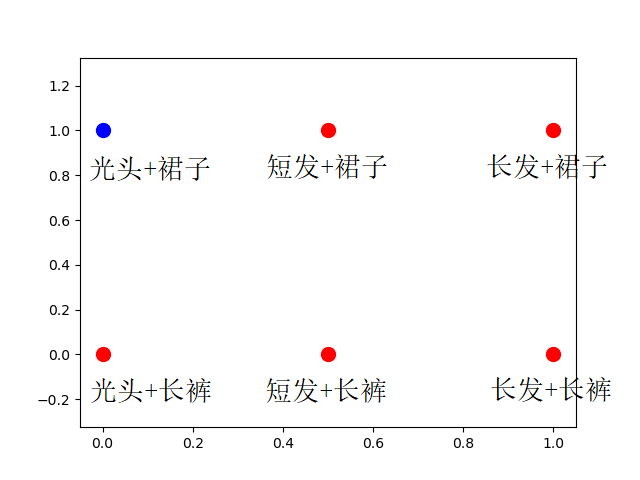
对偶形式的例子,收敛性的证明……



 浙公网安备 33010602011771号
浙公网安备 33010602011771号