LIS 的二分做法

stooooooooooooooooooooooooooo xhr ooooooooooooooooooooooooooooorz

一种是线段树，一种是二分，接下来介绍二分做法。

就是维护一个上升序列，每次加一个元素，具体过程看代码，好理解的（）

说人话就是维护长度为 \(i\) 的最后一个元素的最小值，但是这个维护方法有点 trick。

LIS 的二分做法是个好东西，有时能够给出一种具体的映射。

int LIS(){
    int b[MAXN], top = 0, a[MAXN];
    b[0] = -1;
    for(int i = 1; i <= n; i++){
        if(a[i] > b[top]){
            top++, b[top] = a[i];
        }else{
            int l = 1, r = top;
            while(l < r){             // 二分，O(log n)
                int u = (l + r) >> 1;
                if(a[i] > b[u]){
                    l = u + 1;
                }else{
                    r = u - 1;
                }
            }
            b[l] = a[i];
        }
    }
    return top;
}

三分图（ZR 模拟赛题）

参考：xhr 大神的 20251022 总结的 C 题

xhr 大神的题解（含题意）

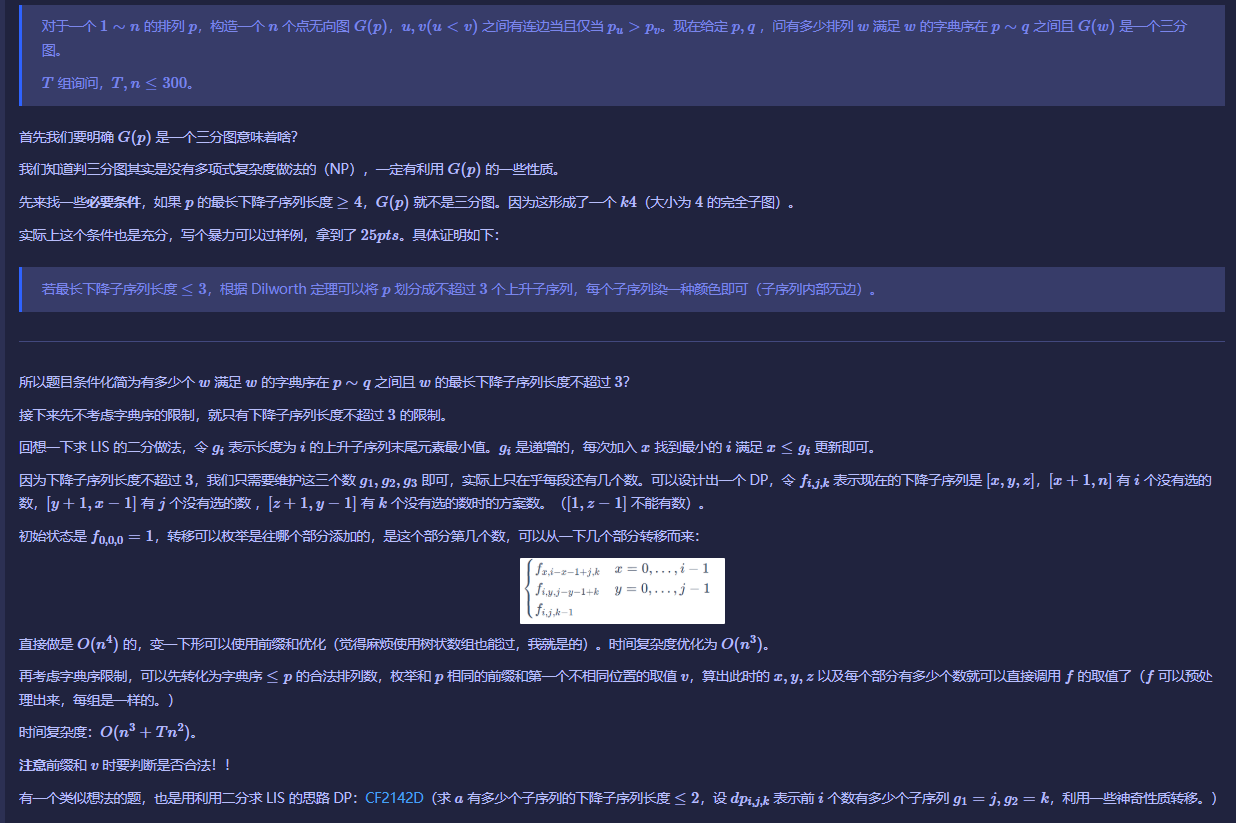
问题是求字典序在 \(p \sim q\) 之间且最长下降子序列 \(\le 3\) 的排列数量。多测，\(1 \le T,n \le 300\)。

差分变为求字典序比一个序列小的合法序列的数量。

考虑枚举公共前缀，再枚举后面一个的值。

考虑维护长度为 \(1,2,3\) 的下降子序列的最大值，但实际上从 LIS 的二分做法来看会更简单：维护下降序列 \(G\)（初始全为 \(+\infty\)），每次在末尾加上 \(x\)，找到最小的 \(i(g_i \le x)\)，然后 \(g_i \leftarrow x\)。

优先优化 check 方法，考虑对一个序列 \(P\) 的 check 方法：

• 设当前 \(g_1=x,g_2=y,g_3=z\)，末尾加入一个数 \(w\)
  • 如果 \(w < z\) 就不合法了。
  • 如果 \(z < w < y\)，则 \(z = w\)。
  • 如果 \(y < w < x\)，则 \(y = w\)。
  • 如果 \(x < w\) 则 \(x = w\)

很显然，这是一个只和大小关系有关的限制条件，恰好，对于相关排列的计数，也只能做到存储大小关系。

那么就不要再考虑存具体的值了，我们在乎的是数量。

• \(f_{i,j,k}\) 表示分别表示 \((+\infty,x),(x,y),(y,z)\) 中的数量，之后全部用完的方案数。
• \(f_{i,j,k} = \sum\limits_{x=1}^{i}{f_{i-x,j+x-1,k}} + \sum\limits_{x=1}^{j}{f_{i,j-x,k+x-1}} + f_{i,j,k-1}\)
• 第一个求和式中为什么是 \(j+x-1\)？因为 \(w\) 操作后就不算了。后面的类似。

前缀和优化可做到 \(O(n^3)\)。

接下来回到询问，\(O(n^2)\) 次枚举，每次确定了 \((x,y,z)\)，那么 \((i,j,k)\) 也确定了。

总时间复杂度 \(O(n^3 + Tn^2)\)。

总之：

• 可见 LIS 的二分做法是个好东西，能够给出一种具体的映射。
• 而且这题的限制只和大小关系有关，需要有能列出条件的好习惯去发现这个。

CF2143D2 - Inversion Graph Coloring (Hard Version)

（这题的原题意类似上面三分图那题，同样的转化得到如下题意）

给一个序列 \(A\)，求有多少个 \(A\) 的子序列，满足最长下降子序列长度 \(\le 2\)。答案对 \(10^9 + 7\) 取模。

多测，\(\sum{n} \le 2000\)。

做法几乎和上面一题一样，梳理 check 做法再 dp。