计算几何入门 

namespace CG{
  struct Node{
    double x, y;
    Node operator- (Node j){ return {x - j.x, y - j.y}; }
  };
  double ABS(double x){ return max(x, -x); } // 实数绝对值 
  int cmp(double x){ return (ABS(x) < 1e-10 ? 0 : (x < 0 ? -1 : 1)); } // 优化精度误差 
  double len(Node x, Node y){ return (x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y); } // 欧几里得距离的平方
  double dot(Node x, Node y){ return x.x * y.x + x.y * y.y; } // 点乘
  double cross(Node x, Node y){ return x.x * y.y - x.y * y.x; } // 叉乘
  double postoeg(Node p, Node a, Node b){ // 点到直线距离
    if(dot(b - a, p - a) < 0) return sqrt(len(p, a));
    if(dot(a - b, p - b) < 0) return sqrt(len(p, b));
    return ABS(cross(p - a, b - a)) / sqrt(len(b, a));
  }
}

宝宝

极坐标系：用旋转角与距离表示维度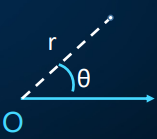image

向量：又被称为矢量，拥有大小和方向的量，但是没有位置属性，符号为 \(\overrightarrow{PQ}\)。

  • 向量的模长就是 \(\sqrt{x^2+y^2}\)。
  • 向量的幅角就是幅角（可以用 C++ 中的 atan2(x, y) 实现，范围 \([-\pi, \pi]\)，常数较大，调用 \(5 \cdot 10^7\) 次要 2s，且小心精度）
  • 类似复数，去看眼 FFT 里的复数部分吧。
  • 关于向量的旋转，考虑复数相乘，设向量的对应复数 \(z = x + yi\)，然后要乘一个 \(z'\) 满足 \(|z'|=1,arg(z')=\theta\)。
    • \(z z' = (x + yi) \times (\cos \theta + i \sin \theta)\)
    • 乘一下得到 \((x \cos \theta - y \sin \theta, x \sin \theta + y \cos \theta)\)

\(\sin \theta\) 等于纵坐标，\(\cos \theta\) 等于横坐标。

简单多边形，顾名思义，就是一个普通多边形，没有自交的多边。

正多边形，所有边都等长的多边形，显然所有内角都相等。

计算几何入门

参考：

点乘：\(\overrightarrow{OA} \cdot \overrightarrow{OB} = A_x \times B_x + A_y \times B_y = |OA| \times |OB| \times \cos(\theta)\)（等于 \(OA\) 投影到 \(OB\) 上的长度，再乘 \(|OB|\)）

叉乘：\(\overrightarrow{OA} \times \overrightarrow{OB} = A_x \times B_y - A_y \times B_x = |OA| \times |OB| \times \sin(\theta)\)（还表示两个向量组成的平行四边形的面积）。

注意 \(\theta\) 是有向角，所以可以用来判线段关系：

  • 叉乘：
    • 为正时 \(\overrightarrow{OA}\) 在 \(\overrightarrow{OB}\) 的左边。
    • 为负时 \(\overrightarrow{OA}\) 在 \(\overrightarrow{OB}\) 的右边。
    • 为 \(0\) 时 \(\overrightarrow{OA}\) 和 \(\overrightarrow{OB}\) 共线。
  • 点乘：
    • 为正时 \(\overrightarrow{OA}\) 和 \(\overrightarrow{OB}\) 一前一后或一上一下
    • 为负时相反。
    • 为 \(0\) 时 \(\overrightarrow{OA}\) 和 \(\overrightarrow{OB}\) 相互垂直。

然后能引申出一些简单应用，例如判断两线段是否平行，还有下面这些。

点、线关系的判断

点 \(O\) 是否在线段 \(PQ\) 上：

  • 要求 \(\overrightarrow{OP} \times \overrightarrow{OQ} = 0\)，且横纵坐标在范围内。

求两直线 \(AB\) 和 \(PQ\) 交点：

  • 先判是否有交。就是判两直线是否平行。
  • 设交点为 \(O\)，有 \(|OP| : |PQ| = S_{PAB} : S_{PAB} + S_{QAB}\)，里面的 \(S\) 用叉乘算（注意取 abs）

线段 \(l_1\) 与线段 \(l_2\) 是否相交（求交点转为直线就是了）：

  • 相交就要求 \(l_1\) 的两端在 \(l_2\) 两侧、\(l_2\) 的两端在 \(l_1\) 两侧。
  • 证明就是分讨。

极角排序

模板题 luogu - T269230 极角排序，简单练习题 luogu - P3476 [POI 2008] TRO-Triangles：

int up(PII x){ return x.second < 0 || (x.second == 0 && x.first < 0); }
LL operator* (PII x, PII y){ return x.first * y.second - x.second * y.first; }

bool cmp(PII x, PII y){
  int ox = up(x), oy = up(y), xc = x * y;
  if(ox != oy) return ox < oy;
  return xc > 0 || (xc == 0 && ojld(x) < ojld(y));
}

判断点是否在简单多边形内

一种是角度法，逆时针枚举边，计算偏角和（注意有正有负）（计算的时候用叉乘和 acos 即可），如图 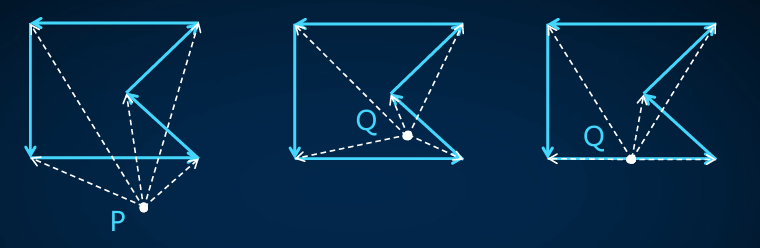image

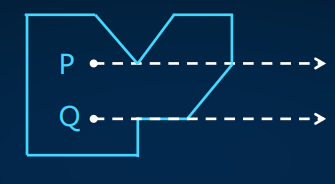
一种是射线法。如图 imageimage

从点向右作出一条射线，判断与多边形的交点数量。每产生一个交点，将会切换在多边形内外的状态。

交点数量为偶数，则点在多边形外；交点数量为奇数，则点在多边形内。但还需要特判在边上的情况。

水平的边不影响状态的变化，直接忽略。经过顶点改变状态时，该顶点必然分别是关联的两条边的上端点和下端点。忽略所有非水平边的上端点。

计算简单多边形面积

选个原点 \(O\)，逆时针枚举边，计算三角形面积，一减一加。如图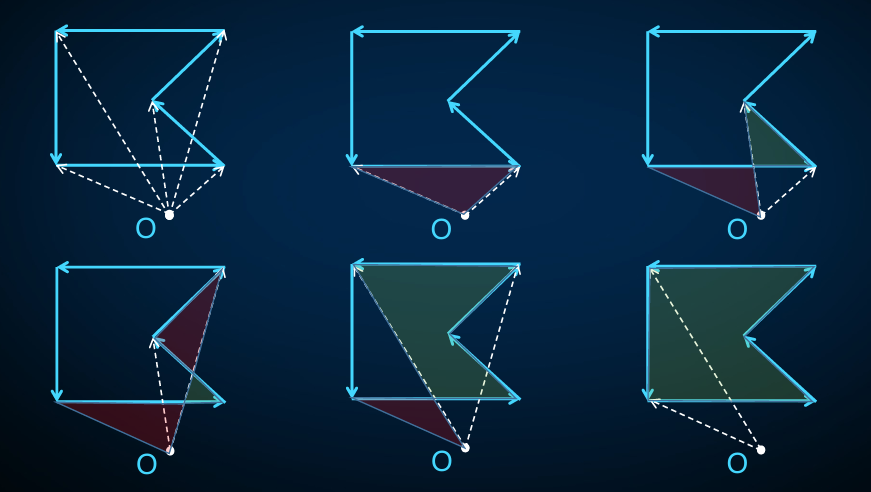：image

大概就是你考虑随便选一个点 \(P\)，对射线 \(OP\)，然后类似射线法。

凸包

凸多边形：所有内角均小于 \(\pi\) 的简单多边形。显然任意对角线均在凸多边形的内部，显然正多边形就是凸多边形。

凸包：包含所有点的最小凸多边形。

凹函数和凸函数不是一个东西，上凸函数就是凹函数，下凸函数就是凸函数（英语里是有 convex（凸） 和 concave（凹） 严格区分的，部分中文材料可能会有混淆）

求凸包模板题 luogu - P2742 【模板】二维凸包，做法：

  • 先选一个一定在凸包上的点，两种方法：
    • 随便找个参照点，然后选距离最远的点。
    • 随便选个参照方向，选在该方向上最远或最近的点。
  • 考虑逆时针，显然可以 \(O(n^2)\) 暴力。每次 \(O(n)\) 找到全局最靠右的点。
  • 可以直接极角排序，优化到 \(O(n \log n)\)。
  • 还可以求下凸壳和上凸壳，再拼起来，这样还是要排序，但不用极角排序（看上去本质是把极角排序分开，实际上是运用了上凸壳这种东西）。

求凸包上最远两点的距离（求凸包直径）（求若干个点的最远点对）（直径表示能够让凸包从任意方向滑动通过的最小宽度） luogu - P1452 【模板】旋转卡壳

  • 对踵点：对于凸包上的一对点，将其连线并在两点作垂线，如果凸包上所有点都在这对平行线之间，则将这对点称为对踵点。
  • 显然暴力是 \(O(n^2)\) 枚举点。并且这个枚举也没有单调性，不能双指针。
  • 考虑一对对踵点，将这一对平行线同步旋转，直到某条平行线与某条边重合。
  • 枚举边，对踵点只可能是最远点（距离这条边）和边的两个端点之一。这还有单调性的，双指针时间复杂度 \(O(n)\)。

求若干个凸多边形的交集的面积 luogu - P4196 【模板】半平面交

  • 相关定义（比较重要）：
    • 半平面：直线一侧的半个平面被称为半平面（可以用开和闭来描述是否包含边界）。
      • 可以通过有向线段的起点、方向确定半平面，当然了半平面与有向线段的长度无关。（默认半平面在有向线段的左边）（也可以将有向线段统称为向量，不过也要注意区分！）
    • 半平面交：半平面的交集。
      • 半平面交得到的多边形必然为凸多边形，注意也可能为无限面积或零（是线或点）或空（注意区分！）
    • 简单多边形的半平面交，称为多边形的核
      • 多边形的核可能不存在，凸多边形的核等于本身。
      • 核内任意点，与多边形内任意点连成的线段，一定在多边形内部。
        • 核内的点能够看见多边形内的每一个点
  • 考虑在半平面交中加入新的半平面。对这个多边形枚举相邻两点，如果这两点被分开了就新建一个点。时间复杂度 \(O(n^2)\)。
  • 注意半平面交中每条边属于一个半平面，且是凸的（不断左旋的），对所有半平面极角排序（注意同向的，要舍弃外面的保留里面的）……\(O(n \log n)\) 好复杂，学不会喵喵喵

练习

luogu - P3217 [HNOI2011] 数矩形

初中几何题。

给若干个点，要选出四个点构成矩形，求矩形的最大面积。

我们要求对角线互相平分，且相等。

所有线段，按照长度和中点分类。对每一类，极角排序，然后双指针即可。

暴力枚举可以直接过。见 https://www.luogu.com.cn/discuss/1232225

posted @ 2026-01-17 15:01  hhhqx  阅读(48)  评论(0)    收藏  举报