关于上台阶问题走法问题进一步思考

原题目就不多赘述了

看了很多文章感觉解释的不是很清楚，直接就告诉你f(x) = f(x - 1) + f(x - 2)这么一个答案，为什么呢？？？

一个台阶走法

0 => 1

两个台阶走法

0 => 1 => 2

0 => 2

三个台阶走法

0 => 1 => 2 => 3

0 => 2 => 3

0 => 1 => 3

我们来倒推：就是最后一步要么走一阶要么走两阶

如果最后一步是走了一个台阶，那么前面的走法是不是和2阶走法一样再加上一个台阶

0 => 1 => 2 加上一步 0 => 1 => 2 => 3

0 => 2 加上一步 0 => 2 => 3

如果我们最后一步是走了两个台阶，是不是和1阶走法一样再加上两个台阶

0 => 1 加上两步 0 => 1 => 3

就可以这里理解

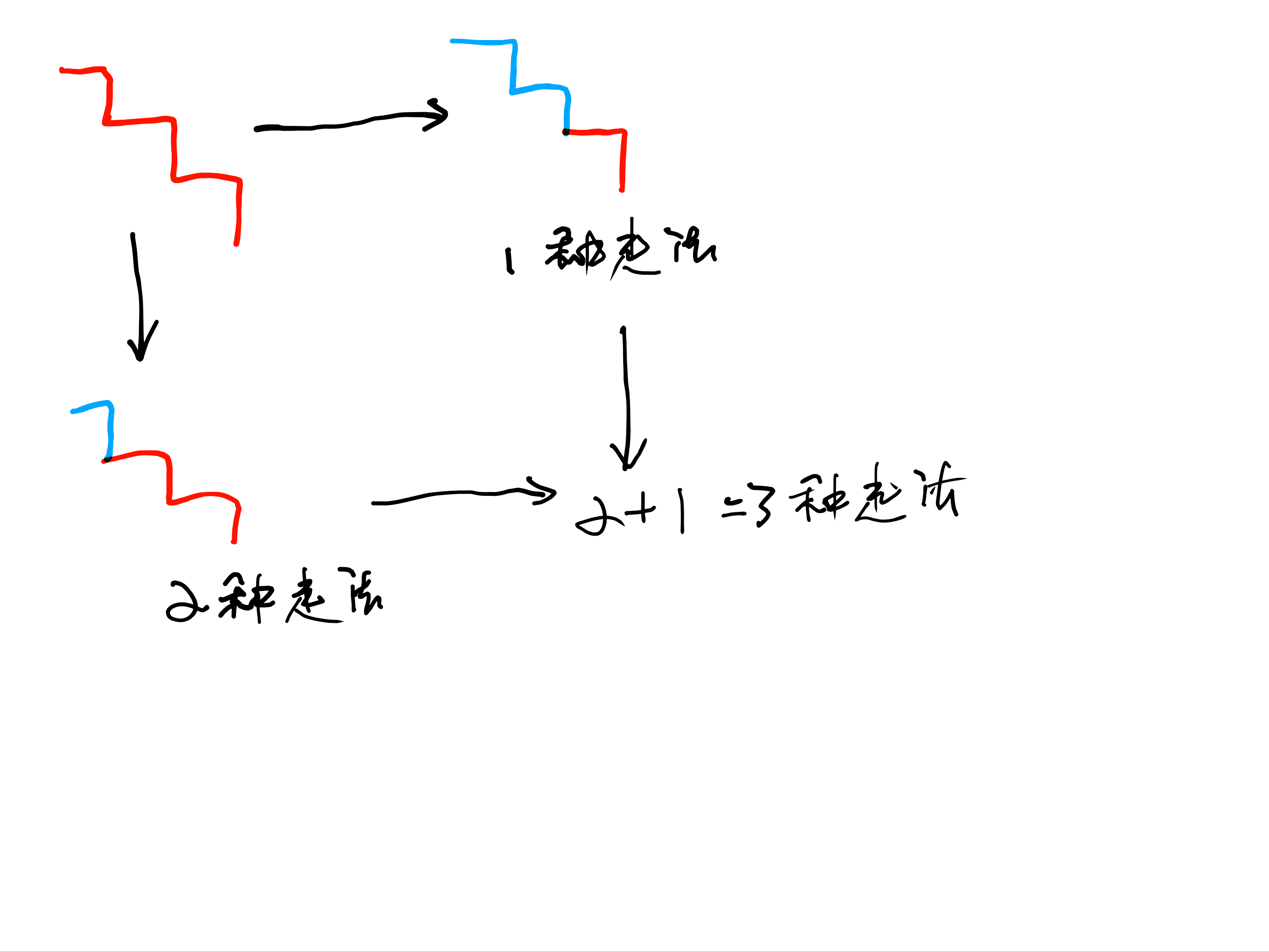
再来看四个台阶走法

0 => 1 => 2 => 3 => 4

0 => 2 => 3 => 4

0 => 1 => 3 => 4

前三种情况是最后一步跨了一个台阶, 前面的三阶走法和3阶走法就是一样的 然后加上一阶

0 => 1 => 2 => 4

0 => 2 => 4

后两次 情况是最后一步跨了两个台阶，前走的两阶走法是不是和两阶走法一样，然后加上两阶

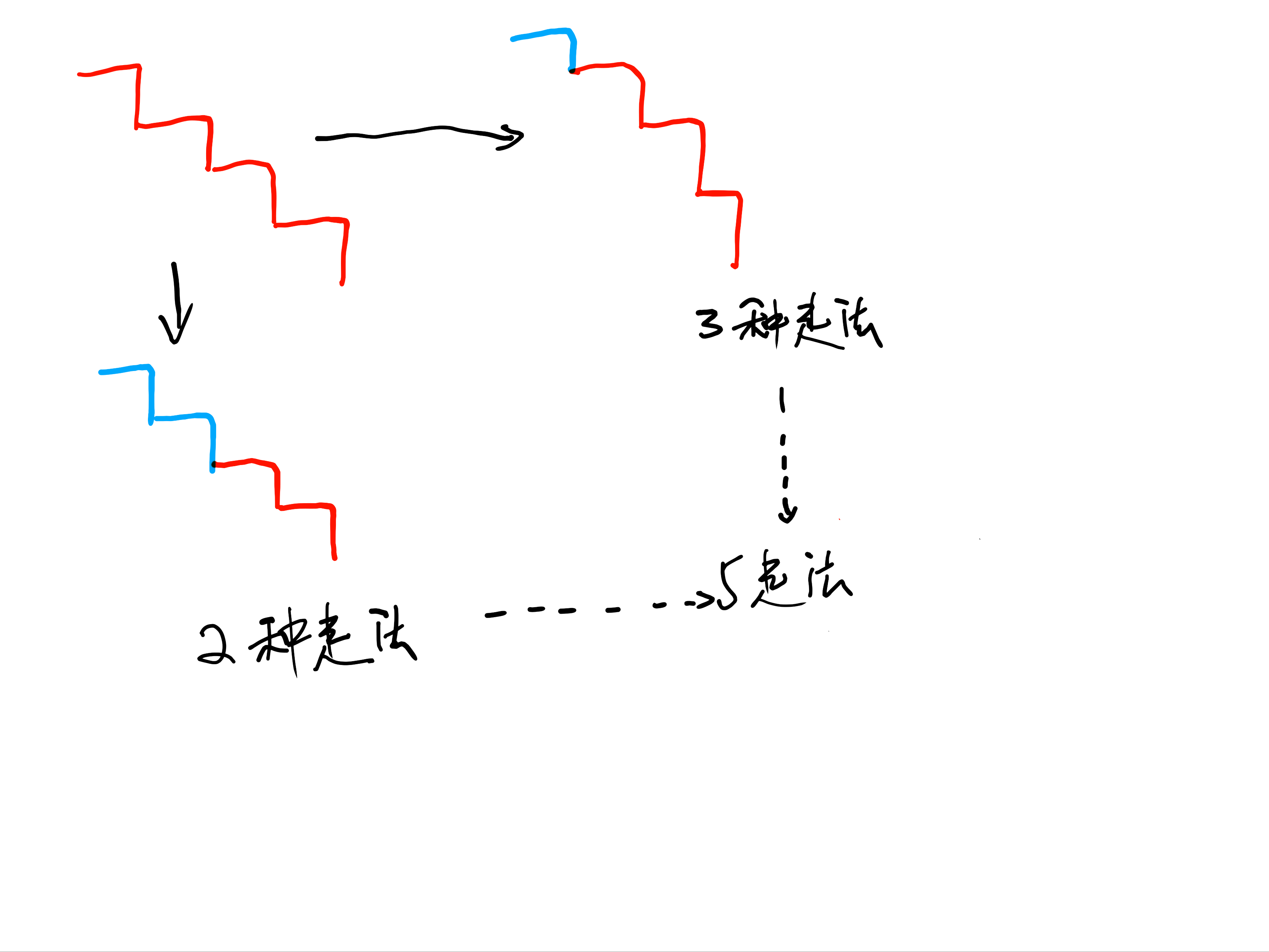
我们来看5阶的走法

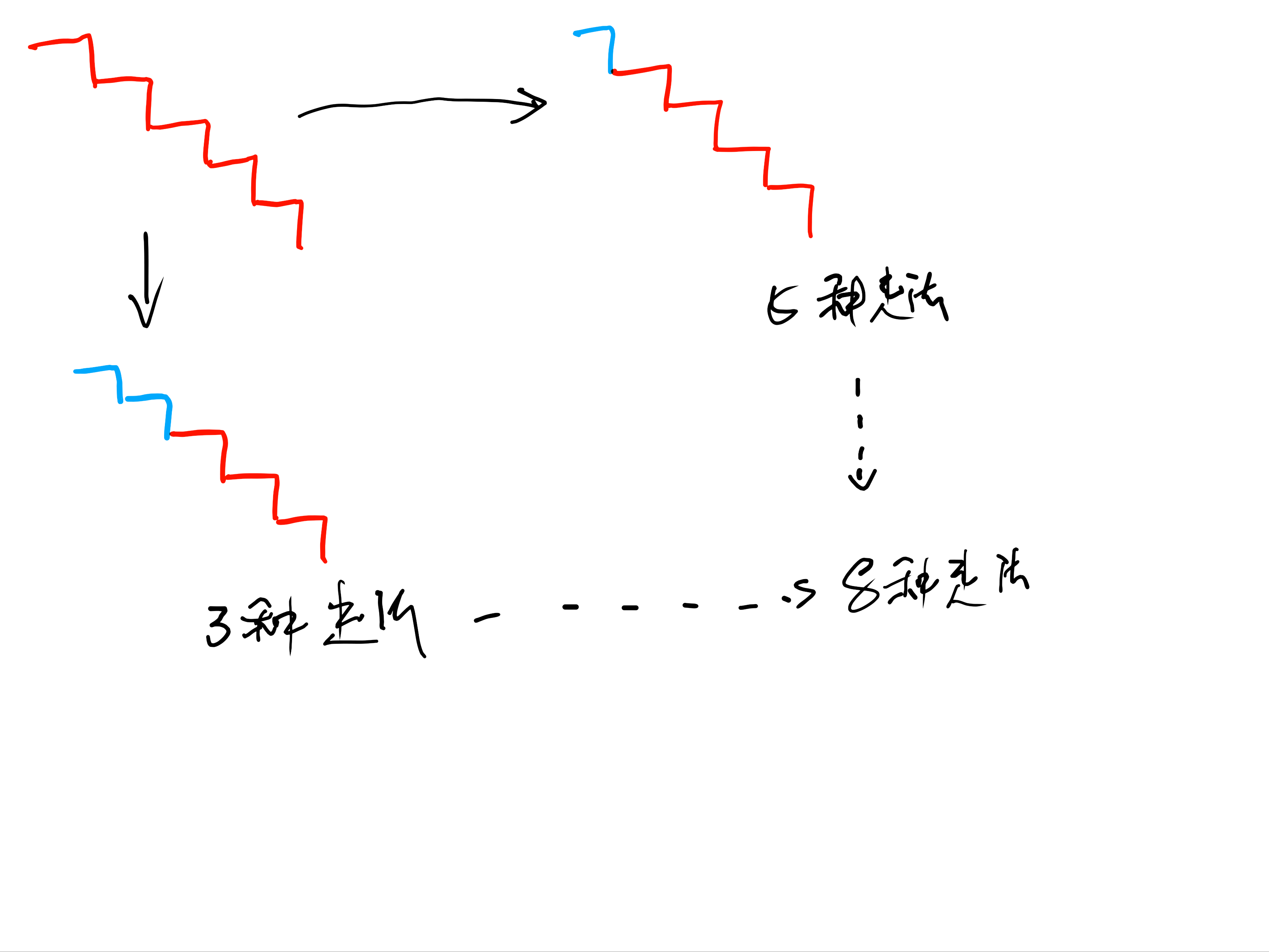
所以我们就可以 通过f(x) = f(x - 1) + f(x -2)

function step (max = 10) {
    let one = ['1'] // 走法
    let two = ['11', '2'] // 走法
    if (max === 1) return one
    if (two === 1) return two
    let i = 3
    while (i <= max) {
        let _one = one.map(v => v + '2') // 最后一步是2
        let _two = two.map(v => v + '1') // 最后一步是1
        let temp = [..._two, ..._one]
        one = two
        two = temp
        i++
    }
    return two
}

我们再衍生就是 比如 有三种走法，一步一阶，一步两阶，一步三阶。无论多少台阶 那我们最后一步的走法都是要么一阶，要么两阶，要么三阶，就可以用f(x) = f(x - 1) + f(x - 2) + f(x - 3)

function step (max = 10) {
    let one = ['1']
    let two = ['11', '2']
    let three = ['111', '21', '12', '3']
    if (max === 1) return one
    if (two === 1) return two
    if (three === 1) return three
    let i = 4

    while (i <= max) {
        let _three = three.map(v => v + '1')
        let _two = two.map(v => v + '2')
        let _one = one.map(v => v + '3')
        let temp = [..._three, ..._two, ..._one]

        one = two
        two = three
        three = temp
        i++
    }
    return three
}
console.log(step(4))
// '1111', '211', '121', '31', '112', '22', '13'
console.log(step(5)) 
'11111', '2111', '1211', '311', '1121', '221', '131', '1112', '212', '122', '32', '113', '23'