上海市计算机学会2025.10月赛丙组T5

题目在这里

9月份的时候打梦熊的某场 \(NOIP\) 模拟赛作为 \(T1\) 出现过，没写出来

题解也没有看懂，感觉很模糊

然后打上海市10月月赛 \(T5\) 又出现了

第一次在比赛中遇到重题，内心充满了激动与绝望

因为还是不会写。。。

理了好几遍思路，终于是可以来写题解了

题解

\[\sum_{i=1}^n \max(0, i - a_i) = \sum_{i=1}^n \sum_{j=i+1}^n [a_i > a_j] \]

观察一下这个式子，左边即是冒泡排序的最优操作次数，右边是逆序对数量，也就是实际操作次数

什么时候冒泡排序达到能达到最优操作次数呢？即任何数字都刚好被交换到指定位置，没有多余交换

举个例子：

\[3,2,1 \]

\[2,3,1 \]

\[2,1,3 \]

\[1,2,3 \]

在这种情况下就是不优的，\(2\) 原来就在正确位置上，却被交换到了第一位一次

我们发现，如果排列的最长下降子序列长度大于或等于 \(3\) 时，是不优的，也就是等式不成立

证明

设原序列有长度为 \(n\) 下降子序列为 \(A_1,A_2,A_3...\) ，则 \(A_1\) 最后一定会被交换到第 \(n\) 项

在这个过程中，第 \(2\) 到 \(n-1\) 都会被向左交换一次

但第 \(2\) 到 \(n-1\) 项都还与 \(A_n\) 存在逆序对，肯定还要被向右交换至少一次

第 \(2\) 到 \(n-1\) 项都被重复交换了，这当中至少有一个元素，所以

\[2 \leq n-1 \]

\[n \ge 3 \]

---

那也就是求在长度为 \(n\) 的排列中，最长下降子序列长度不超过 \(2\) 的排列数量

考虑动态的向末尾加入数，建立一个集合 \(S\) 表示所有还未被加入的数

设当前已加入的数中的最大值为 \(x\)

1.加入一个比 \(x\) 小的数：

此时只能加 \(S\) 中最小的元素，若加入非最小元素，则最小元素一定会出现在后面

此时 \(x\) ，当前加入元素，最小元素构成长度为 \(3\) 的下降子序列

2.将最大值修改为一个比它更大的值

如果修改的不是最大值，又会有较小的值往后放，形成长度为三的下降子序列

该最大值改大是不会有影响的，同理只要改小后仍然是最大值也能改

但当前状态本来就是由较小的状态转移而来，所以不需要往小转移

---

设计状态 \(f_{i,j}\) 表示已加入 \(i\) 个数字，当前最大值为 \(j\)

则 \(f_{i,j}\) 可以向 \(f_{i+1,j}\) 和 \(f_{i,j+k}\) 转移，其中 \(i>j\) 的状态不存在

我们可以参考 \(shopping\,\,\,plans\) 类题的思路，考虑简化转移过程，到 \(f_{i,j+k}\) 可以由好几次 \(f_{i,j+1}\) 拼凑而来

我们发现它变成了一个在网格图中从 \((1,1)\) 走到 \((n,n)\) 的方案数问题

因为 \(i>j\) 的状态不存在，所以路径当中不得越过 \(i=j\) 的对角线

这不就是卡特兰数吗？接下来考虑怎么处理固定前缀

先看前缀是否合法，即其最长下降子序列长度是否大于或等于 \(3\) ，若前缀不合法，直接输出 \(0\)

直接计算其最长下降子序列的长度，这个可以在 \(O(n\,\,log\,\,n)\) 内实现，\(O(n\,\,log\,\,n)\) 求最长下降子序列

然后把前缀总结成一个状态，即取其长度与最大值，也就是说将上述问题改为指定起点计算就可以了

在这个问题中卡特兰数应该怎么用呢？参考原来卡特兰数在该问题中的推导方法

不超过直线 \(y=x\) ，也就是至少碰到一次 \(y=x+1\)

那么只要计算这些碰到 \(y=x+1\) 的方案个数，参考反射法

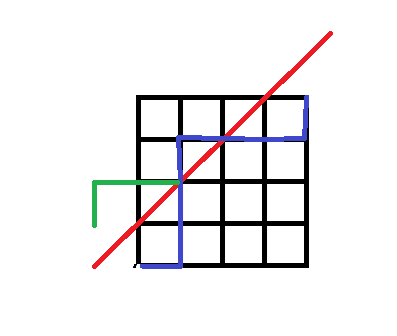
将在碰到 \(y=x+1\) 之前的部分作关于 \(y=x+1\) 的镜面反射，得到此时的起点由 \((0,0)\) 变成 \((-1,1)\)

所以卡特兰数的计算公式为 \(C_{2n}^n-C_{2n}^{n-1}\)

现在的问题也是同理，可以将起点 \((u,v)\) 通过反射转为 \((v-1,u+1)\)

该问题计算公式即为：

\[C_{n-u+n-v}^{n-v}-C_{n-(v-1)+n-(u+1)}^{n-(u-1)} \]

化简：

\[C_{2n-u-v}^{n-v}-C_{2n-u-v}^{n-u+1} \]

带入原问题中 \(u,v\) 分别是合法前缀中的最大值和合法前缀的长度

注意需要特判 \(n=m\) 的情况

CODE

#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxn=5e5+5;
const int mod=1e9+7;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=(x<<3)+(x<<1)+c-48;
	x=(f ? -x : x);
}
int n,m;
int a[maxn];
LL fpow(LL x,int y){
	LL ans=1;
	while(y){
		if(y&1) ans=ans*x%mod;
		y>>=1,x=x*x%mod;
	}
	return ans;
}
LL ww(int x){
	LL ans=1;
	for(int i=1;i<=x;i++) ans=ans*i%mod;
	return ans;
}
LL C(int x,int y){
	return ww(x)*fpow(ww(x-y),mod-2)%mod*fpow(ww(y),mod-2)%mod;
}
int main(){
	//freopen("nene.in","r",stdin);
	//freopen("nene.out","w",stdout);
	read(n),read(m);
	bool f=0;
	int u=m,v=0;
	vector<int> p;
	for(int i=1;i<=m;i++){
		read(a[i]);
		int j=upper_bound(p.begin(),p.end(),-a[i])-p.begin();
		if(j==(int)p.size()){
			p.push_back(-a[i]);
			if(p.size()==3) f=1;
		}
		else p[j]=-a[i];
		v=max(v,a[i]);
	}
	if(f) printf("0");
	else if(n==m) printf("1");
	else printf("%lld",(C(2*n-u-v,n-v)-C(2*n-u-v,n-u+1)+mod)%mod);
	return 0;
}
//^o^