8.15HL day5 NOIP模拟赛
T1手推打表 \(20min\) 毫无发现
T2 \(5min\) 思路+ \(30min\) 代码+\(2h\)调试(状态转移写错+topo入度写错)
T3,T4 \(20min\) 观察,并打了T3的暴力(太急了st板子打错了)
回去看T1并打了暴力(模数打成\(98244353\)了),打完发现杨辉三角,此时还剩 \(10min\)
拼手速失败,\(0+100+0+0=100pts\) 被自己气笑了
以下为T1-T3题解
T1

观察一下每个 \(a_1\) 在每个前缀和中的每一项的出现次数
即定义 \(f_{i,j}\) 为第 \(i\) 重前缀和的第 \(j\) 个数中 \(a_1\) 的出现次数,得到下表
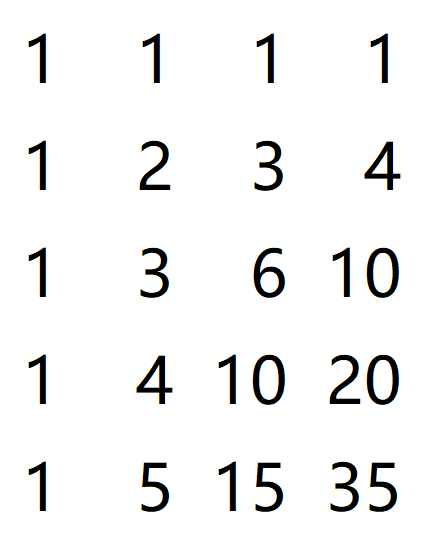
转移方程为 \(f_{i,j}=f_{i-1,j}+f_{i,j-1}\) ,是不是有点眼熟?
画几条分割线就明白了

看到了吗?杨辉三角形
通过杨辉三角的通项公式,即第 \(i\) 行的第 \(j\) 个为\(C_{i-1}^{j-1}\)
例如我们要求第五重前缀和,则第一位至第四位系数依次为:
\(C_{4}^{0}=1\) \(C_{5}^{1}=5\) \(C_{6}^{2}=15\) \(C_{7}^{3}=35\)
\(a_2,a_3,...\) 这些的系数只要把整个 \(a_1\) 系数表对应的进行向右位移即可
#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxn=5005;
const int maxm=1e7+maxn+5;
const int mod=998244353;
void read(int& x){
char c;
bool f=0;
while((c=getchar())<48) f|=(c==45);
x=c-48;
while((c=getchar())>47) x=x*10+c-48;
x=(f ? -x : x);
return;
}
LL fac[maxm];
int a[maxn],g[maxn];
LL ans[maxn];
int n,m;
LL fpow(LL x,int y){
LL res=1;
while(y){
if(y&1) res=res*x%mod;
x=x*x%mod,y>>=1;
}
return res;
}
LL C(int x,int y){
return fac[x]*fpow(fac[x-y],mod-2)%mod*fpow(fac[y],mod-2)%mod;
}
int main(){
//freopen("prefix.in","r",stdin);
//freopen("prefix.out","w",stdout);
read(n),read(m);
for(int i=1;i<=n;i++) read(a[i]);
fac[0]=1;
for(int i=1;i<=1e7+maxn;i++) fac[i]=fac[i-1]*i%mod;
for(int i=1;i<=n;i++) g[i]=C(m+i-2,i-1);
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){
ans[j]=(ans[j]+1ll*g[j-i+1]*a[i]%mod)%mod;
}
}
for(int i=1;i<=n;i++){
printf("%lld ",ans[i]);
}
return 0;
}
//^o^
T2

转化问题,我们只要求路径上的严格次大值即可
常见的思路,先 \(tarjan\) 缩点然后跑拓扑排序,这里讲一下状态转移
维护两个 \(dp\) 数组,\(dp1\) 到这一点的所有路径中最大值,\(dp2\) 到这一点的最大合法次大值
为什么不直接最大值和次大值呢?因为这样的话有可能最大值和次大值不在同一条路径上,就不对了
转移:首先 \(dp2_v=max(dp2_v,dp2_u)\) \(dp1_v=max(dp1_v,dp1_u)\)
如果发现当前点权大于 \(dp1_u\) ,那么可以将 \(dp1_u\) 作为合法次大值
如果发现当前点权小于 \(dp1_u\) ,则可以将当前点权作为合法次大值
得到状态转移代码:
dp1[v]=max(dp1[v],dp1[u]);
dp2[v]=max(dp2[v],dp2[u]);
if(mx[v]>dp1[u]) dp2[v]=max(dp2[v],dp1[u]);
if(mx[v]<dp1[u]) dp2[v]=max(dp2[v],mx[v]);
#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxn=2e5+5,maxm=1e6+5;
void read(int& x){
char c;
bool f=0;
while((c=getchar())<48) f|=(c==45);
x=c-48;
while((c=getchar())>47) x=x*10+c-48;
x=(f ? -x : x);
return;
}
class mmap{
public:
int head[maxn],nxt[maxm],e[maxm];
int mp_cnt;
mmap(){
memset(head,-1,sizeof(head));
mp_cnt=-1;
}
void add_edge(int u,int v){
e[++mp_cnt]=v;
nxt[mp_cnt]=head[u];
head[u]=mp_cnt;
}
}mp1,mp2;
int n,m,q,s;
int a[maxn];
int mx[maxn],smx[maxn];
int dp1[maxn],dp2[maxn];
//dp1到这一点的最大值,dp2到这一点的最大次大值
int in[maxn];
int dfn[maxn],low[maxn],g[maxn];
bool ins[maxn],vis[maxn];
stack<int> st;
int cnt=0,tot=0;
void update(int u,int x){
if(mx[u]<x) smx[u]=mx[u],mx[u]=x;
else if(smx[u]<x&&x<mx[u]) smx[u]=x;
}
void tarjan(int u){
dfn[u]=low[u]=++cnt;
ins[u]=1,st.push(u);
for(int i=mp1.head[u];~i;i=mp1.nxt[i]){
int v=mp1.e[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(ins[v]){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
++tot;
int now=-1;
while(now!=u){
now=st.top(),st.pop();
ins[now]=0,g[now]=tot;
update(tot,a[now]);
}
}
}
void dfs(int u){
vis[u]=1;
dp1[u]=mx[u],dp2[u]=smx[u];
for(int i=mp2.head[u];~i;i=mp2.nxt[i]){
int v=mp2.e[i];
++in[v];
if(vis[v]) continue;
dfs(v);
}
}
void topo(){
queue<int> q;
q.push(g[s]);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=mp2.head[u];~i;i=mp2.nxt[i]){
int v=mp2.e[i];
--in[v];
dp1[v]=max(dp1[v],dp1[u]);
dp2[v]=max(dp2[v],dp2[u]);
if(mx[v]>dp1[u]) dp2[v]=max(dp2[v],dp1[u]);
if(mx[v]<dp1[u]) dp2[v]=max(dp2[v],mx[v]);
if(!in[v]){
q.push(v);
}
}
}
}
int main(){
//freopen("mod.in","r",stdin);
//freopen("mod.out","w",stdout);
read(n),read(m),read(q),read(s);
for(int i=1;i<=n;i++){
read(a[i]);
}
int u,v;
for(int i=1;i<=m;i++){
read(u),read(v);
mp1.add_edge(u,v);
}
memset(mx,-1,sizeof(mx));
memset(smx,-1,sizeof(smx));
for(int i=1;i<=n;i++){
if(!dfn[i]){
tarjan(i);
}
}
for(int i=1;i<=n;i++){
u=i;
for(int j=mp1.head[u];~j;j=mp1.nxt[j]){
v=mp1.e[j];
if(g[u]!=g[v]){
mp2.add_edge(g[u],g[v]);
}
}
}
dfs(g[s]);
topo();
while(q--){
read(u);
u=g[u];
if(!vis[u]) printf("-1\n");
else if(dp2[u]==-1) printf("0\n");
else printf("%d\n",dp2[u]);
}
return 0;
}
//^o^
T3

计数题,设计一个 \(dp_i\) 表示以第 \(i\) 位结尾的合法数列个数
然后分别求出每个 \(a_i\) \(b_i\) 的靠左第一个大于它的,靠右第一个大于等于它的(防止重复)
然后进行区间统计,详见代码
注意每个数字也可以去继承它前面的最大值,找到满足 \(max(a_i,b_i)<max(a_j,b_j)\) 的最大 \(j\),然后加上 \(dp_j\)
#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxn=1e5+5;
void read(int& x){
char c;
bool f=0;
while((c=getchar())<48) f|=(c==45);
x=c-48;
while((c=getchar())>47) x=x*10+c-48;
x=(f ? -x : x);
return;
}
int n;
int a[maxn],b[maxn],c[maxn];
int la[maxn],ra[maxn],lb[maxn],rb[maxn],kk[maxn];
int t1[maxn],t2[maxn];
LL dp[maxn];
void getl(int* p,int* ans){
stack<int> st;
for(int i=1;i<=n;i++){
while((!st.empty())&&p[st.top()]<=p[i]) st.pop();
if(!st.empty()) ans[i]=st.top()+1;
else ans[i]=1;
st.push(i);
}
}
void getr(int* p,int* ans){
stack<int> st;
for(int i=1;i<=n;i++){
while((!st.empty())&&p[st.top()]<=p[i]){
ans[st.top()]=i-1;
st.pop();
}
st.push(i);
}
while(!st.empty()){
ans[st.top()]=n;
st.pop();
}
}
int main(){
//freopen("seqmax.in","r",stdin);
//freopen("seqmax.out","w",stdout);
read(n);
for(int i=1;i<=n;i++) read(a[i]);
for(int i=1;i<=n;i++) read(b[i]);
for(int i=1;i<=n;i++) c[i]=max(a[i],b[i]);
getl(a,la),getr(a,ra),getl(b,lb),getr(b,rb),getl(c,kk);
LL ans=0;
for(int i=1;i<=n;i++){
t1[a[i]]=t2[b[i]]=i;
if(a[i]>=b[i]){
int j=t2[a[i]];
if(j>=la[i]&&rb[j]>=i) dp[i]+=j-max(la[i],lb[j])+1;
}
else{
int j=t1[b[i]];
if(j>=lb[i]&&ra[j]>=i) dp[i]+=j-max(lb[i],la[j])+1;
}
dp[i]+=dp[kk[i]-1];
ans+=dp[i];
}
printf("%lld",ans);
return 0;
}
//^o^


 浙公网安备 33010602011771号
浙公网安备 33010602011771号