8.11

HL集训day1，周赛

场切A-D，已补E

A

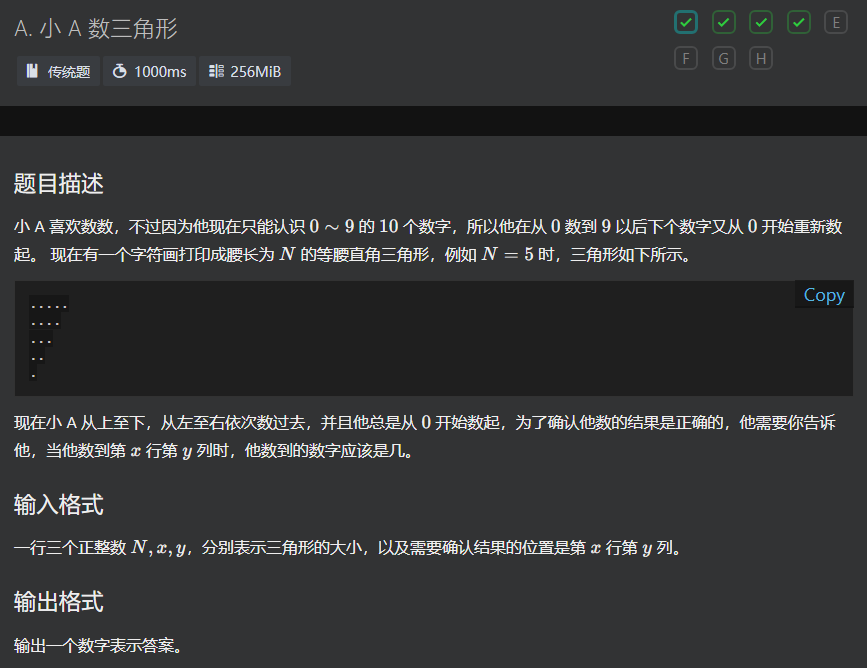
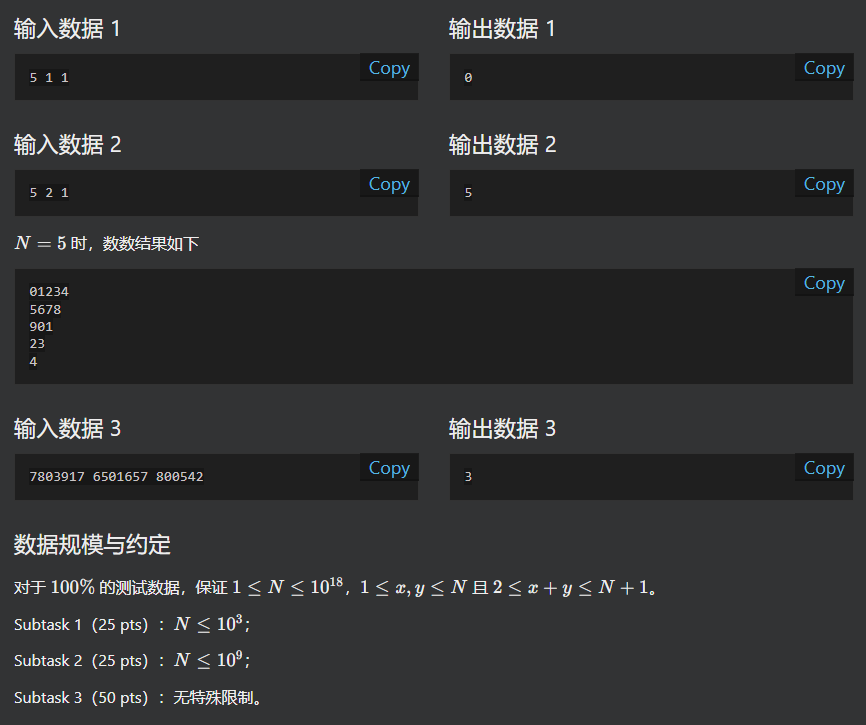
因为数据范围卡了一会

由题意，只要求第x行第y列是第几个.就可以了

前面的用高斯定理，首相为n，末项为n-x+2，项数为x-1，由于数据范围较大，需要及时取模，但2关于10又不存在逆元

观察发现，n-x+2+n和x-1两项中必有一个偶数，判断哪个是偶数，先把它除掉，就可以在过程中及时取模了

代码有点乱

#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
void read(LL& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	x=(f ? -x : x);
	return;
}
LL n,x,y;
int main(){
	read(n),read(x),read(y);
	int ans;
	if((n-x+2+n)%2==0) ans=((1ll*((n-x+2+n)/2%10)*((x-1)%10))%10+y-1)%10;
	else ans=((1ll*((n-x+2+n)%10)*((x-1)/2%10))%10+y-1)%10;
	printf("%d",ans);
	return 0;
}
//^o^

B

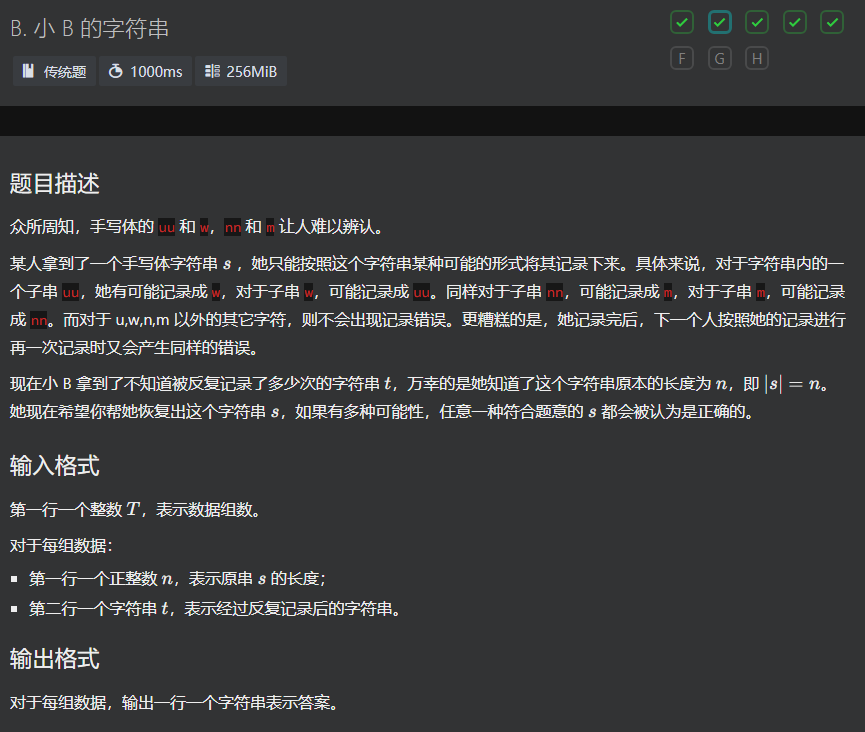
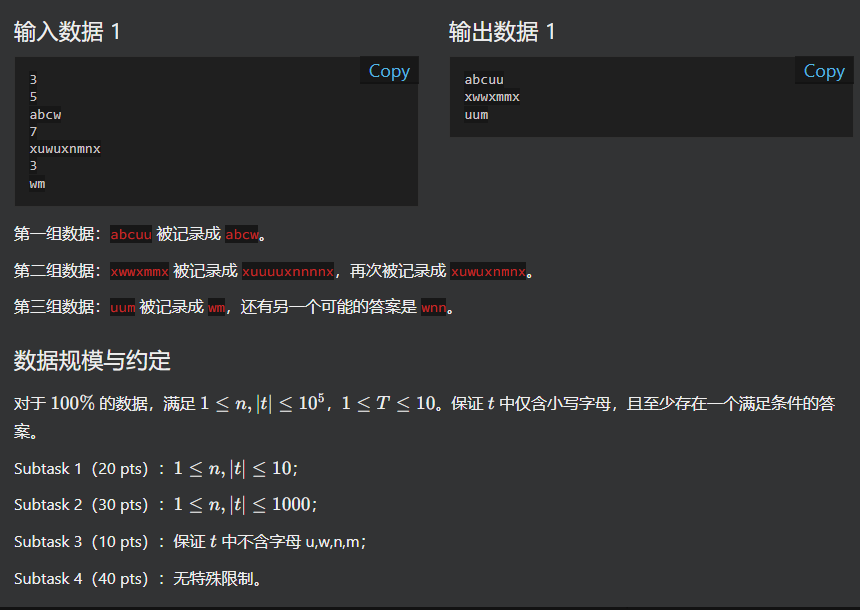
把所有w和m都展开成uu和vv，然后再从左向右缩，发现长度合法的时候输出就好了

#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	x=(f ? -x : x);
	return;
}
string s,si,ans;
int t,n;
int main(){
	read(t);
	while(t--){
		read(n);
		cin>>s;
		si.clear(),ans.clear();
		for(int i=0;i<s.size();i++){
			if(s[i]=='w') si.append("uu");
			else if(s[i]=='m') si.append("nn");
			else si.append(1,s[i]);
		}
		int cnt=si.size();
		for(int i=0;i<si.size();i++){
			if(i!=si.size()-1&&cnt>n&&si[i]==si[i+1]&&(si[i]=='u'||si[i]=='n')){
				--cnt;
				++i;
				if(si[i]=='u') ans.append(1,'w');
				else ans.append(1,'m');
			}
			else ans.append(1,si[i]);
		}
		cout<<ans<<endl;
	}
	return 0;
}
//^o^

C

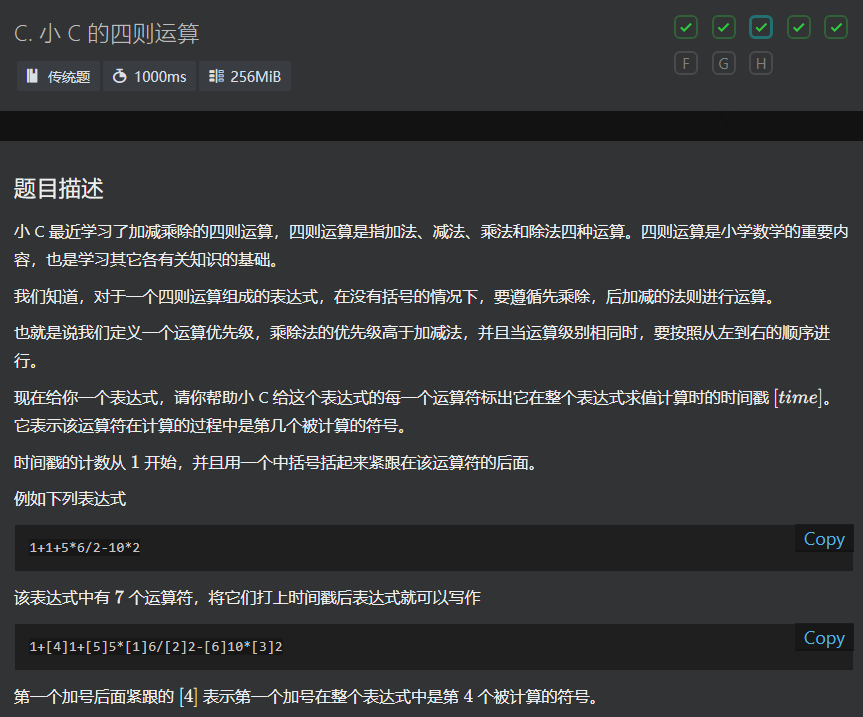
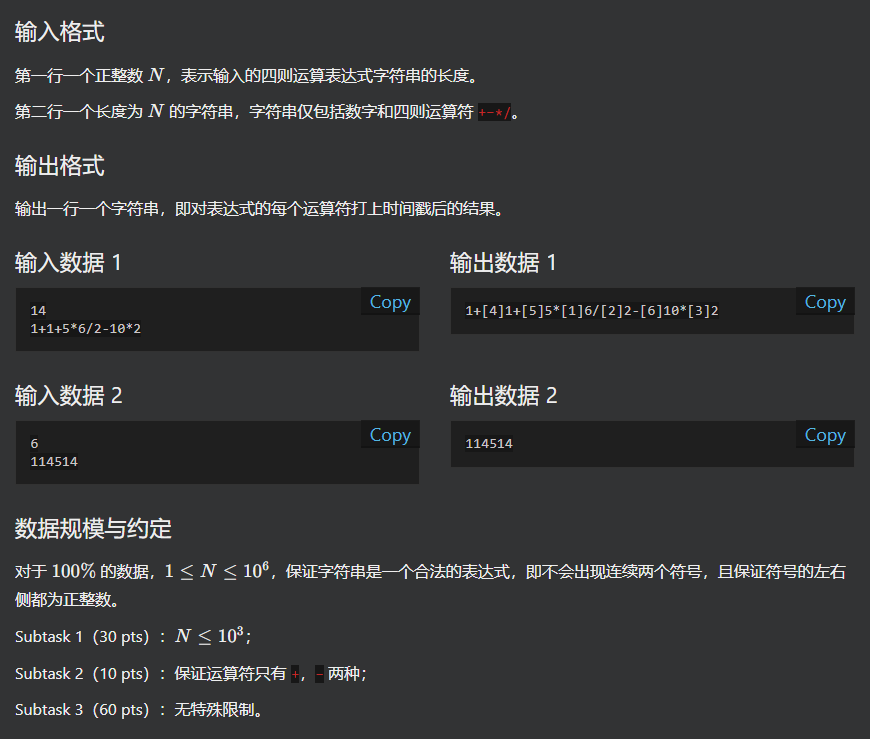
扫两边就好，第一遍编号乘除，第二遍编号加减

#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	x=(f ? -x : x);
	return;
}
string s;
int n;
int ans[maxn];
int main(){
	read(n);
	cin>>s;
	int cnt=0;
	for(int i=0;i<s.size();i++){
		if(s[i]=='*'||s[i]=='/') ans[i]=++cnt;
	}
	for(int i=0;i<s.size();i++){
		if(s[i]=='+'||s[i]=='-') ans[i]=++cnt;
	}
	for(int i=0;i<s.size();i++){
		cout<<s[i];
		if(ans[i]) cout<<'['<<ans[i]<<']';
	}
	return 0;
}
//^o^

D

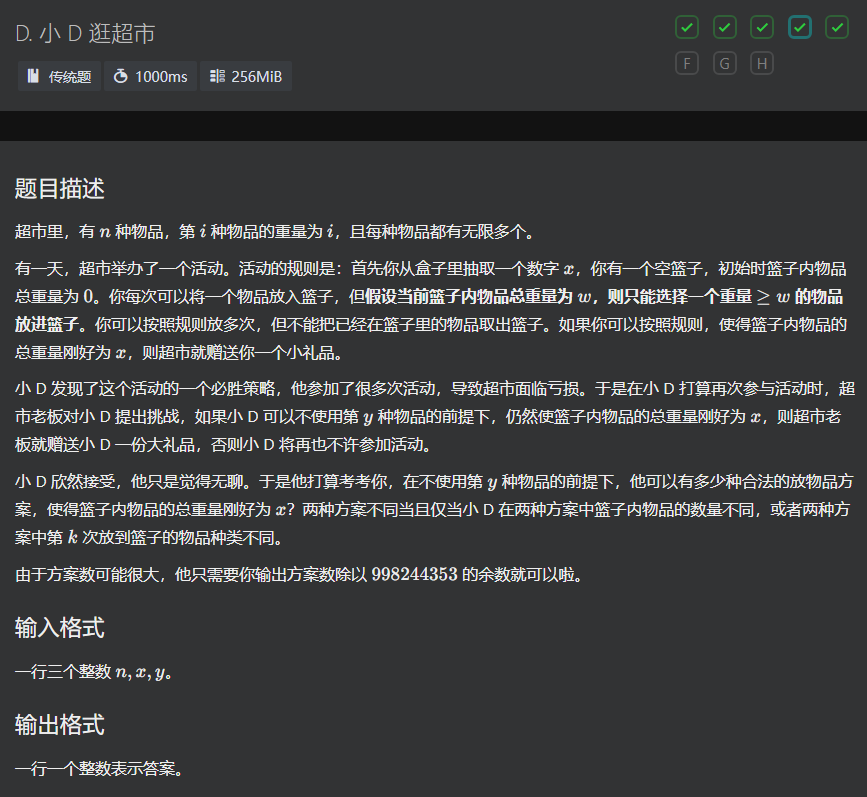
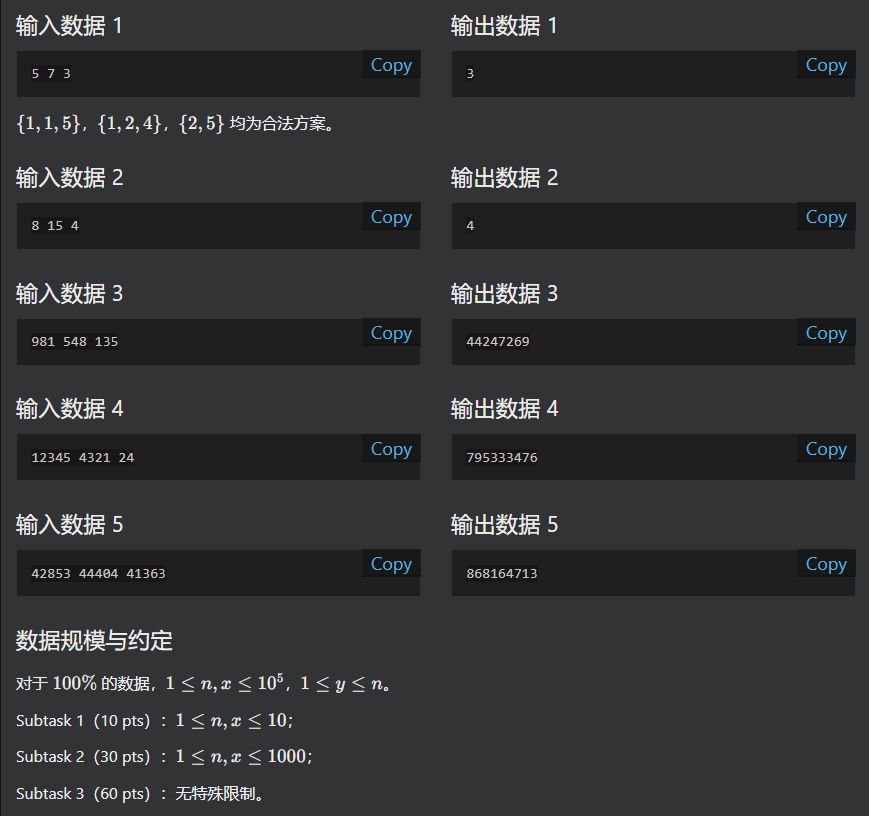
想到动态规划

放哪一类物品只与当前篮子的总重量有关

设计状态dp[i]表示凑成总重为i的方法数量有多少种

转移：因为新放入的物品重量要大于当前篮子的总重，物品重量下限为ceil(i/2)

特判如果此时放入物品重量为y，跳过该过程

一共只有n种物品，重量上限为n

由于i-ceil(i/2)=floor(i/2)

得到状态转移

for(int j=max(i-n,0);j<=i/2;j++){
  if(i-j==y) continue;
  dp[i]+=dp[j];
}

由于是连续区间，可以用前缀和优化，维护dp数组的前缀和sum，加上取模

int r=i/2,l=i-n;
dp[i]=(sum[r]-(l-1<0 ? 0 : sum[l-1])+mod)%mod;
if(i-y>=l&&i-y<=r) dp[i]=(dp[i]-dp[i-y]+mod)%mod;
sum[i]=(sum[i-1]+dp[i])%mod;

注意初始sum[0]=1,dp[0]=1

#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxm=1.1e6+5;
const int mod=998244353;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	x=(f ? -x : x);
	return;
}
int n,x,y;
LL dp[maxm];
LL sum[maxm];
int main(){
	read(n),read(x),read(y);
	sum[0]=1,dp[0]=1;
	for(int i=1;i<=x;i++){
		int r=i/2,l=i-n;
		dp[i]=(sum[r]-(l-1<0 ? 0 : sum[l-1])+mod)%mod;
		if(i-y>=l&&i-y<=r) dp[i]=(dp[i]-dp[i-y]+mod)%mod;
		sum[i]=(sum[i-1]+dp[i])%mod;
	}
	printf("%lld",dp[x]);
	return 0;
}
//^o^

E

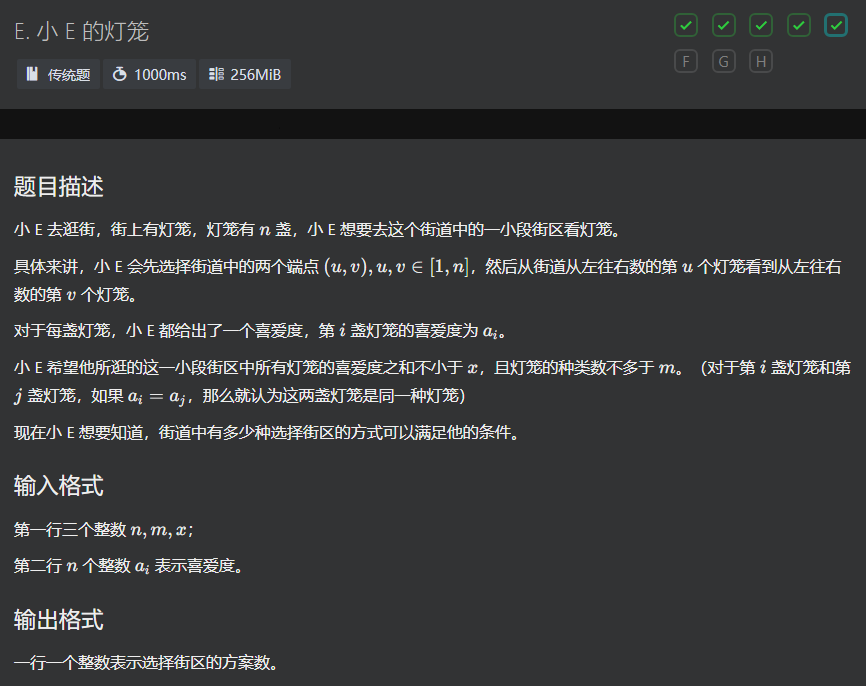
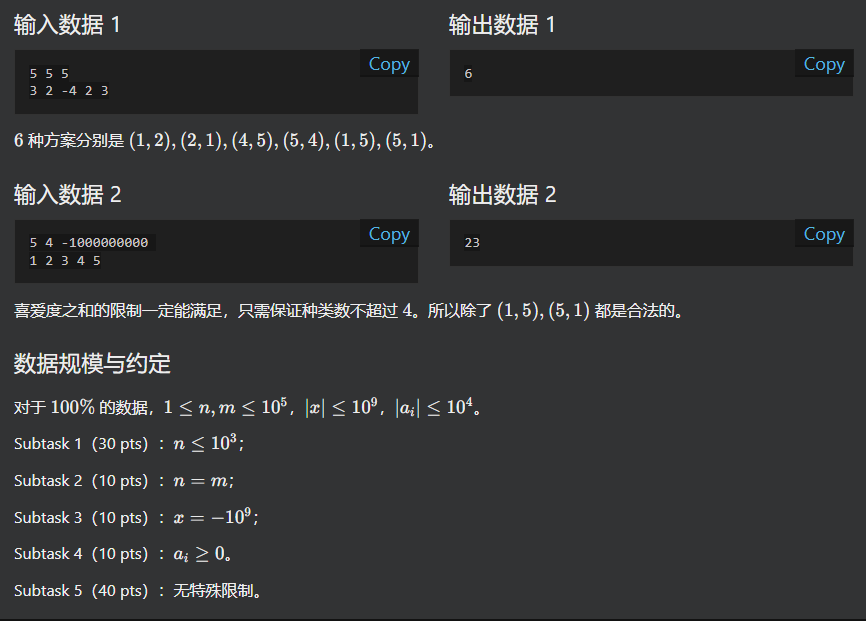
先处理种类数：

用双指针扫出所有种类数为m的区间，即以每个数字为结尾的，记以第i个结尾的区间的左端点为l[i]

维护前缀和数组sum[i]，转变问题为寻找区间l[i]到i之间sum[i-1]-sum[j]>=x的j的个数

把i按sum[i]排序后放入树状数组，由上述式子推得sum[i]-sum[j+1]>=x，枚举i，统计区间内的个数

#include<bits/stdc++.h>
#define fst first
#define sec second
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
typedef pair<int,LL> auther;
const int maxn=1e5+5;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	x=(f ? -x : x);
	return;
}
void read(LL& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	x=(f ? -x : x);
	return;
}
bool cmp(auther a,auther b){
	return a.sec<b.sec;
}
int n,m,x;
int a[maxn];
int l[maxn];
int f[maxn];
int lowbit(int x){
	return x&(-x);
}
void add(int x,int p){
	for(int i=x;i<=maxn;i+=lowbit(i)){
		f[i]+=p;
	}
}
int query_t(int x){
	int ans=0;
	for(int i=x;i>=1;i-=lowbit(i)){
		ans+=f[i];
	}
	return ans;
}
int query(int l,int r){
	return query_t(r)-query_t(l-1);
}
unordered_map<int,int> t;
auther b[maxn];
int main(){
	read(n),read(m),read(x);
	LL dans=0;
	for(int i=1;i<=n;i++){
		read(a[i]);
		if(a[i]>=x) ++dans;
		b[i].sec=b[i-1].sec+a[i];
		b[i].fst=i;
	}
	int p=1,cnt=0;
	for(int i=1;i<=n;i++){
		cnt+=(++t[a[i]]==1);
		while(p<=n&&cnt>m) cnt-=(--t[a[p++]]==0);
		l[i]=p;
	}
	sort(b,b+n+1,cmp);//实际上，第零项是应该存在的，由于前缀和有负数，所以得把0也排进去
	int j=-1;
	LL ans=0;
	for(int i=0;i<=n;i++){
		while(j<n&&b[i].sec-b[j+1].sec>=x) add(b[++j].fst+1,1);
		ans+=query(l[b[i].fst],b[i].fst);
	}
	printf("%lld",ans*2-dans);
	return 0;
}
//^o^