树链剖分学习笔记
此处为重链剖分
例题洛谷P3384
本篇学习笔记围绕模板题展开
一些概念
重儿子 :包含节点数量最多的子节点(仅一个)
轻儿子 :其它非重儿子的子节点
重链 :从一个节点顺着其重儿子向下走所形成的链
重链剖分就是把整棵树分成一条条的链(指从上往下的链)
这些块上的节点经过重新编号后会形成一个连续的数列,从而组成多个连续的区间
这样我们就可以在线段树上去维护一些操作了
怎么分链
在重链上走,相当于每次子树的大小就除以2,所以考虑以重链分链,轻儿子单独成链
没看懂很正常,我也不知道怎么在讲代码之前说的非常清楚,请结合代码阅读
明确前置条件
1.每个节点的子树大小,深度,父亲节点(处理路径和子树内操作有用),重儿子节点,在dfs1内解决
2.每个节点的新编号(dfs序),转移点权,节点所属链的顶端(便于后期操作时的跳跃操作,从当前点直接跳到链顶)
注意每次先遍历重儿子,使得重链上的点编号连续,组成一个连续的区间
查询,操作子树
由于我们是按照dfs序编号的,一颗子树内的所有节点一定组成一个连续的区间
该区间为 \(id[u],id[u]+s[u]-1\),其中 \(s[u]\) 表示子树的大小,\(id[u]\) 表示节点的新编号(dfs序)
查询,操作路径
在链上进行跳跃,链顶深度最大的点优先跳至链顶的父亲节点,直到两点处于同一链上
同一链上的子节点的编号是连续的,于是可以在跳跃过程中将路径拆分成好几个区间,对这些区间进行操作即可
CODE
#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
const int maxn=1e5+5;
void read(int& x){
char c;
bool f=0;
while((c=getchar())<48) f|=(c==45);
x=c-48;
while((c=getchar())>47) x=x*10+c-48;
x=(f ? -x : x);
return;
}
int head[maxn],nxt[maxn<<1],e[maxn<<1];
int w[maxn],wt[maxn];
int mp_cnt;
void init_mp(){
memset(head,-1,sizeof(head));
mp_cnt=-1;
}
void add_edge(int u,int v){
e[++mp_cnt]=v;
nxt[mp_cnt]=head[u];
head[u]=mp_cnt;
}
int t[maxn<<2],laz[maxn<<2];
int n,q,rt,mod;
void push_up(int u){
t[u]=t[u<<1]+t[u<<1|1];
t[u]%=mod;
}
void push_down(int l,int r,int u){
if(!laz[u]) return;
int mid=(l+r)>>1;
t[u<<1]=(t[u<<1]+1ll*(mid-l+1)*laz[u])%mod;
t[u<<1|1]=(t[u<<1|1]+1ll*(r-mid)*laz[u])%mod;
laz[u<<1]=(laz[u<<1]+laz[u])%mod;
laz[u<<1|1]=(laz[u<<1|1]+laz[u])%mod;
laz[u]=0;
}
void build(int l=1,int r=n,int u=1){
if(l==r){
t[u]=w[l]%mod;
return;
}
int mid=(l+r)>>1;
build(l,mid,u<<1),build(mid+1,r,u<<1|1);
push_up(u);
}
void update(int L,int R,int p,int l=1,int r=n,int u=1){
if(l>R||r<L) return;
if(l>=L&&r<=R){
t[u]+=1ll*(r-l+1)*p%mod;
laz[u]+=p%mod;
return;
}
int mid=(l+r)>>1;
push_down(l,r,u);
update(L,R,p,l,mid,u<<1),update(L,R,p,mid+1,r,u<<1|1);
push_up(u);
}
int query(int L,int R,int l=1,int r=n,int u=1){
if(l>R||r<L) return 0;
if(l>=L&&r<=R) return t[u];
int mid=(l+r)>>1;
push_down(l,r,u);
return (query(L,R,l,mid,u<<1)+query(L,R,mid+1,r,u<<1|1))%mod;
}
int dep[maxn],f[maxn],s[maxn];
int hs[maxn],tp[maxn];
int id[maxn];
int dfs_cnt=0;
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,s[u]=1;
for(int i=head[u];~i;i=nxt[i]){
int v=e[i];
if(v==fa) continue;
dfs1(v,u);
s[u]+=s[v];
if(s[v]>=s[hs[u]]) hs[u]=v;
}
}
void dfs2(int u,int t){
tp[u]=t,id[u]=++dfs_cnt,w[dfs_cnt]=wt[u];
if(hs[u]) dfs2(hs[u],t);
for(int i=head[u];~i;i=nxt[i]){
int v=e[i];
if(v!=f[u]&&v!=hs[u]){
dfs2(v,v);
}
}
}
void update_edge(int u,int v,int p){
while(tp[u]!=tp[v]){
if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
update(id[tp[u]],id[u],p);
u=f[tp[u]];
}
if(dep[u]<dep[v]) swap(u,v);
update(id[v],id[u],p);
}
void update_tree(int u,int p){
update(id[u],id[u]+s[u]-1,p);
}
int query_edge(int u,int v){
int ans=0;
while(tp[u]!=tp[v]){
if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
ans=(ans+query(id[tp[u]],id[u]))%mod;
u=f[tp[u]];
}
if(dep[u]<dep[v]) swap(u,v);
ans=(ans+query(id[v],id[u]))%mod;
return ans;
}
int query_tree(int u){
return query(id[u],id[u]+s[u]-1);
}
int main(){
read(n),read(q),read(rt),read(mod);
for(int i=1;i<=n;i++) read(wt[i]);
int u,v;
init_mp();
for(int i=1;i<n;i++){
read(u),read(v);
add_edge(u,v),add_edge(v,u);
}
dfs1(rt,rt),dfs2(rt,rt);
build();
int p,op;
while(q--){
read(op);
if(op==1){
read(u),read(v),read(p);
update_edge(u,v,p);
}
if(op==2){
read(u),read(v);
printf("%d\n",query_edge(u,v));
}
if(op==3){
read(u),read(p);
update_tree(u,p);
}
if(op==4){
read(u);
printf("%d\n",query_tree(u));
}
}
return 0;
}
树链剖分码量较大,有以下注意点:
不要学我线段树写错了找了半个小时
1.\(dfs1\) 和 \(dfs2\) 参数不同,请勿混淆,建议加上 \(1\),这样就算递归写错了编译器也能找出来
2.前置量很多,不要忘记求,图和线段树的大小不要开错
关于时间复杂度:
初始化:
线段树建树 \(O(n\;log\;n)\)
操作:
瓶颈是在路径的修改和查询,跳跃的时间复杂度为 \(O(log\;n)\) ,线段树的查询为 \(O(log\;n)\)
复杂度为 \(O(m \; log^2 n)\) ,\(m\) 为操作数量
边权转点权
\(update\;on\;2025.8.20\)
每个节点只会有一个父节点,也就是说它只存在一条边通向它的父节点
那么我们可以把边权变为其两个点中深度较大的那一个的点权,在 \(dfs2\) 的时候直接赋值新点权
其中根节点的点权为 \(0\)
void dfs2(int u,int t){
dfn[u]=++cnt,tp[u]=t;
if(hs[u]) dfs2(hs[u],t);
for(int i=head[u];~i;i=nxt[i]){
int v=e[i];
if(v==f[u]) continue;
if(v!=hs[u]) dfs2(v,v);
w[dfn[v]]=wt[i];//wt为该边边权
}
}
接下来考虑路径查询/修改时应该怎么改
对于一条路径,起始点和终点的最近公共祖先的点权,即路径中深度最小的点,是不应该被计算进去的。
即发现当两点在同一链上时会产生影响,设点 \(x\) 为 \(x,y\) 两点中深度较小的那一个,则我们不应该计算它的点权
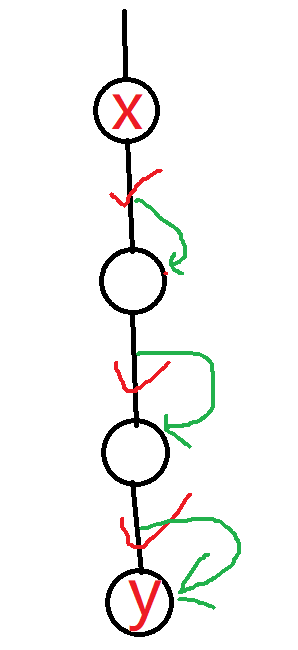
(红勾表示需要计算的边,绿色箭头表示每条边所对应的点)
具体修改如下
int query_edge(int x,int y){
int ans=0;
while(tp[x]!=tp[y]){
if(dep[tp[x]]<dep[tp[y]]) swap(x,y);
ans+=query(dfn[tp[x]],dfn[x]);
x=f[tp[x]];
}
if(dep[x]<dep[y]) swap(x,y);
ans+=query(dfn[y]+1,dfn[x]);//这里改了
return ans;
}
void update_tree(int u,int p){
update(id[u]+1,id[u]+s[u]-1,p);
}
其它照常即可


 浙公网安备 33010602011771号
浙公网安备 33010602011771号