NOIP模拟赛中的一道不知名题目（没有找到原题）

题面在洛谷U314191 暗恋

没有学过基环树专题，求环的方式比较奇特（也许？），

没有说明连通，所以是个森林。

思路

所以原题怎么转换为基环树森林呢？
将暗恋关系转换为有向边，（不要傻傻建图，每条边只有一个出度，直接保存to[i]就可以了）
会发现每一个连通块（用dsu求连通块）中必有一个环，并且有可能有一些通向环的边，可能存在分支

具体如图所示

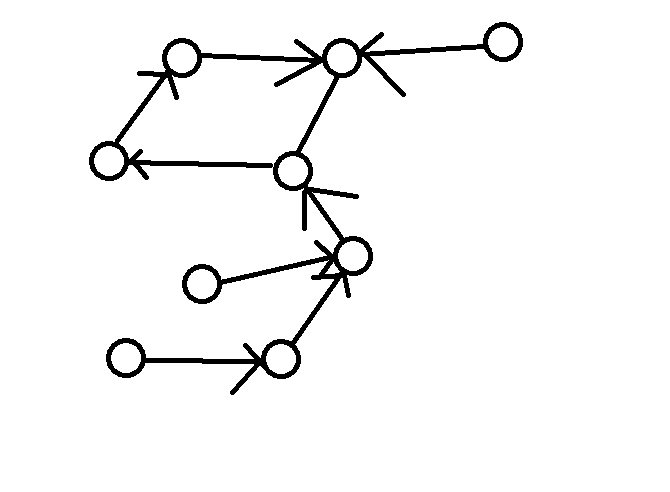
先考虑一颗基环树，记该基环树点的数量为n

若该基环树只有一个环，那么它的答案显然为满足n-1个需求，n种排列方式

第一问求最多能满足的需求数量，因为每个人只暗恋一个人，而可能受到多个或没有人的暗恋（即一个点只有一个出度，但有任意个入度）
所以答案明显就是那些能被暗恋的人的数量，记每个点的入度为p[i]，若p[i]不为0，答案+1,记答案为ans

第二问可以考虑把图分块，然后排列组合。
能分出块的数量就是n-ans（一条边连起两个点，连通块数量-1），分块后再排列组合，即乘上fac[n-ans]

怎么计算分块的数量？

如果是一条链，那就只有一个分块（这只是个例子）
所以分支节点（即有多个入度的节点）是分块关键

画个图想一下（文字说不清楚），记on为环上分支节点的入度的乘积，off为非环上分支节点的入度的乘积
所以分块数量为(on-1)*off（排除环为一个块的情况）

所以第二答案表达为(on-1)*off*fac[n-ans]

合并

有一个注意点，每一个小的分块是可以穿插在一起的，所以统计的时候应记录n-ans的和，最后乘上其阶乘

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const int mod=1e9+7;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=x*10+c-48;
	return;
}
int to[maxn];
int fa[maxn],s[maxn];//fa用于并查集，s记录每个连通块的大小
int p[maxn],ans[maxn],vis[maxn];
int on[maxn],off[maxn];
bool cir[maxn],h[maxn];//cir记录是否在环上，h记录是否是环
long long sum=0;
long long mul=1;
int n,cirp=0;
int find_f(int x){
	if(fa[x]==x) return x;
	else return fa[x]=find_f(fa[x]);
}
void init_dsu(int n){
	for(int i=1;i<=n;i++) fa[i]=i;
}
void merge(int u,int v){
	int a=find_f(u),b=find_f(v);
	if(a!=b) fa[a]=fa[b];
	return;
}
bool dfs(int u){
	vis[u]=1;
	if(p[u]!=1) h[find_f(u)]=0;//如果连通块中有点入度不为0，那就绝对不是环了
	int v=to[u];
	if(vis[v]){
		cirp=v;
		cir[u]=1;
		return 1;
	}
	cir[u]=dfs(v);
	if(u==cirp) return 0;
	else return cir[u];
}
int main(){
	//freopen("single.in","r",stdin);
	//freopen("single.out","w",stdout);
	//corner case?
	read(n);
	init_dsu(n);
	for(int i=1;i<=n;i++){
		read(to[i]);
		merge(i,to[i]);
		++p[to[i]];
	}
	for(int i=1;i<=n;i++){
		int j=find_f(i);
		if(j==i){
			h[i]=1,cirp=-1;
			dfs(i);
			if(h[i]) --ans[i];
		}
		if(p[i]) ++ans[j];
	}//找环
	fill(on+1,on+n+1,1),fill(off+1,off+n+1,1);
	for(int i=1;i<=n;i++){
		int j=find_f(i);
		++s[j];
		if(cir[i]) on[j]=(LL)on[j]*(LL)p[i]%mod;
		else if(p[i]) off[j]=(LL)off[j]*(LL)p[i]%mod;
	}
	int sump=0;
	for(int i=1;i<=n;i++){
		if(find_f(i)==i){
			if(h[i]) mul=mul*s[i]%mod;
			else{
				mul=mul*(on[i]-1)%mod*off[i]%mod;
				sump+=s[i]-ans[i];//合并阶乘
			}
			sum+=ans[i];
		}
	}
	for(int i=1;i<=sump;i++) mul=1ll*mul*i%mod;
	printf("%lld %lld",sum,mul);
	return 0;
}

代码中可能有一些意义不明的语句或变量（应该没了），是前调（shi）试（shan）代码留下的，欢迎指出