KMP学习笔记

KMP最重要的是前缀数组的思想，要考肯定也不会来考模板题。

什么是前缀数组？

pi[i]表示从1到i的子串中，满足第1到k位所组成的子串与第i-k+1到i位所组成的子串相同的最大的k

例如

红色部分就是代表pi[6]=2，其前后公共部分就是AB

蓝色部分就是代表pi[7]=1，其前后公共部分就是A

怎么求pi?

我们不妨把每个pi[i]都列出来，观察一下规律

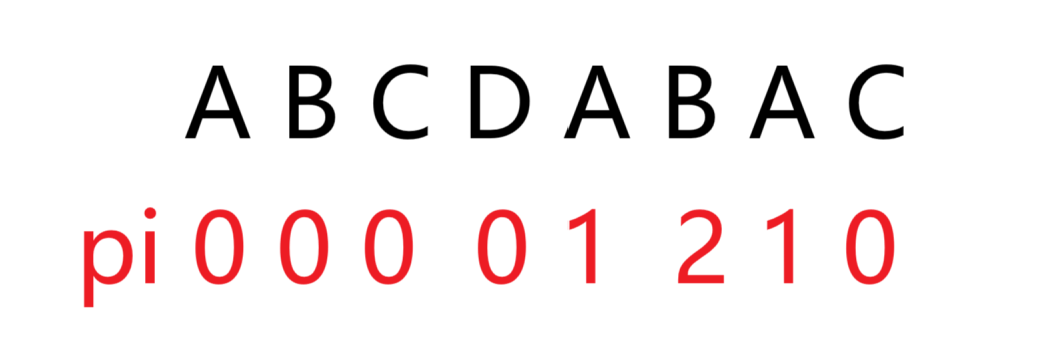
再多列举一些，就会发现，每个pi[i]与pi[i-1]至多只会增加1

对于增加1的情况（例如pi[5]和pi[6])，如果发现两个指针（对于pi[5]来说，就是1和5），向后移一位后相同（s[2]==s[6])，就说明pi[6]=pi[5]+1

如果不一样呢？ 如果一个个往后枚举匹配，时间复杂度又会降到 O(n*n) ，这显然不是我们想要的

因为此时新的匹配部分的长度肯定小于pi[i-1]，但我们真的需要一个个去枚举吗？

不需要，pi[i-1]部分前后匹配部分是相同的，相当于在右边部分向后添加了一个新的字符

左边部分想满足和右边部分匹配，就得先满足在没有添加前是匹配的，但当前pi[i-1]的已经不匹配了

就退而求其次，下一个能做到在i-1范围内匹配的是什么呢？就是pi[pi[i-1]](好好想想）

如此一直向后退，直到找到pi[pi[i-1]]+1这一位能与i这一位匹配为止

处理细节会在代码中展示

//下标从0开始
p[0]=0;
for(int i=1,j=0;i<m;i++){//j表示左边匹配部分的右端，也就是匹配部分的长度
	while(j&&c[j]!=c[i]) j=pi[j-1]; //如果向后找到了0,停止寻找
	if(c[i]==c[j]) ++j;//与右边部分最后一位的匹配要加上
    pi[i]=j;
}

KMP

说了这么多，那KMP与前缀数组有什么关系呢？

例如如下匹配问题
（看一遍就懂了，这里没难度）

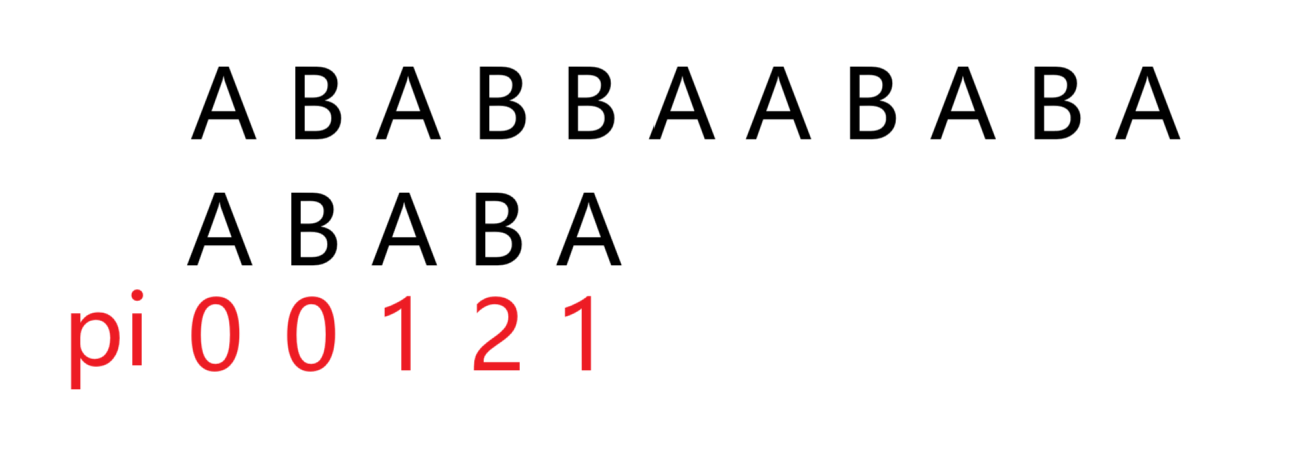
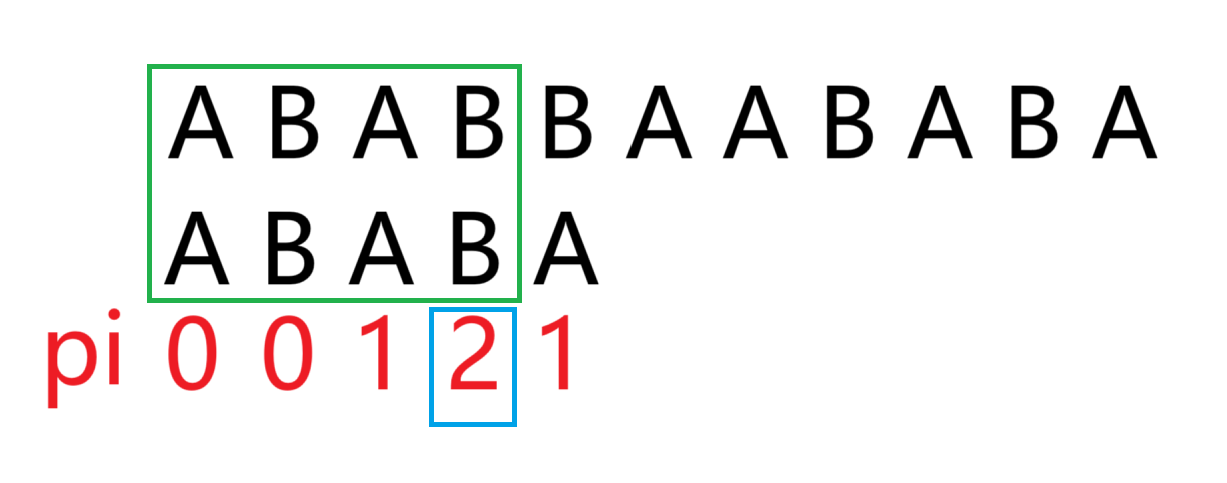
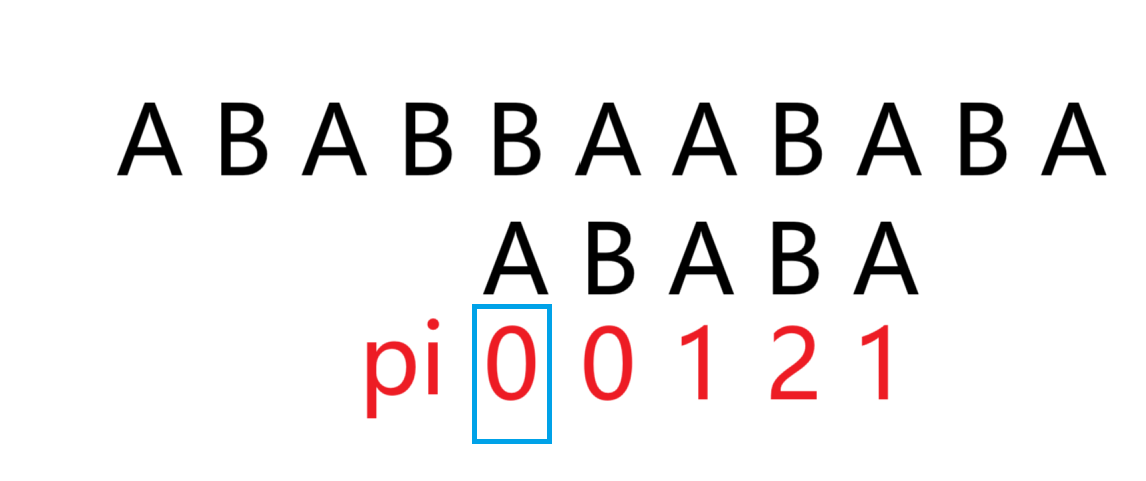
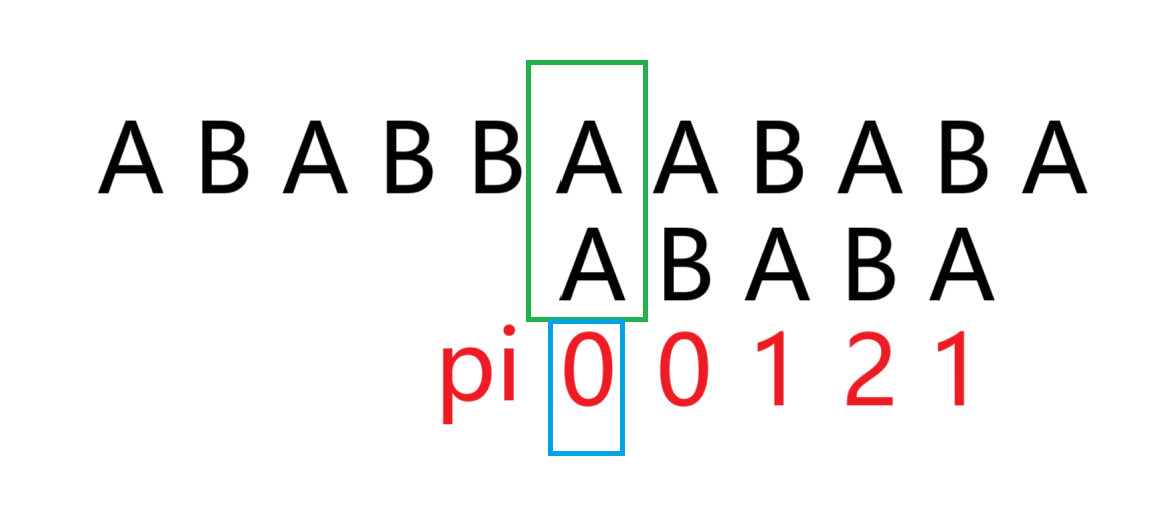
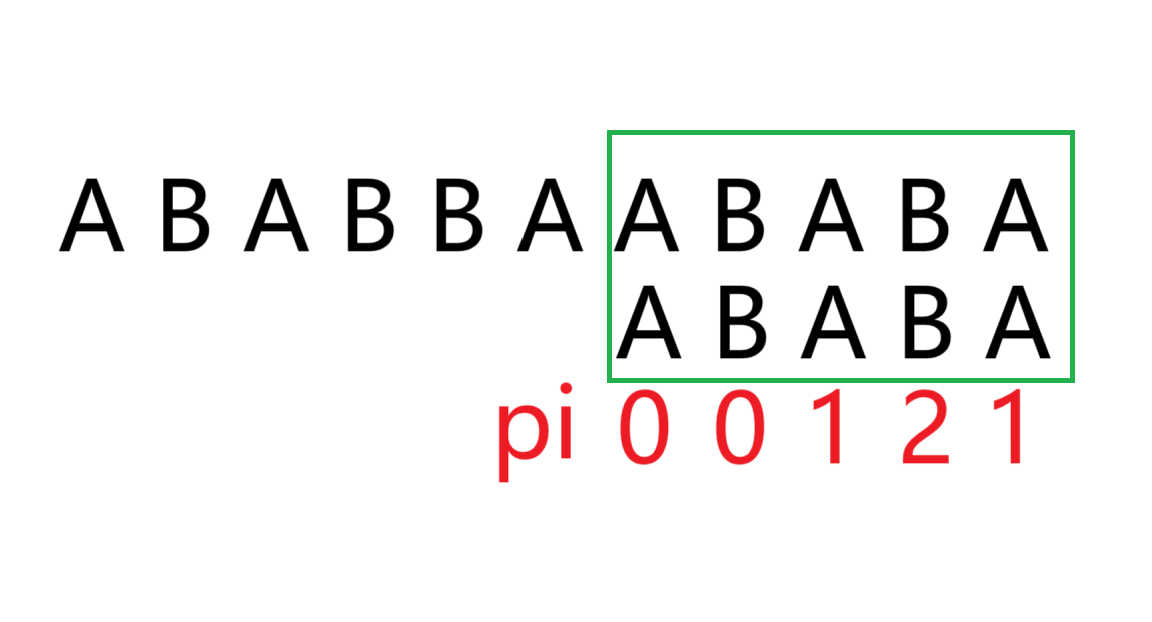
抱歉，修正一下，pi数组应为0 0 1 2 3而不是0 0 1 2 1

代码（洛谷P3375)

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int pi[maxn];
char s[maxn];
char c[maxn];
int n;
int main(){
	scanf("%s",s);
	scanf("%s",c);
	int n=strlen(s),m=strlen(c);
	pi[0]=0;
	for(int i=1,j=0;i<m;i++){
		while(j&&c[j]!=c[i]) j=pi[j-1];
		if(c[i]==c[j]) ++j;
		pi[i]=j;
	}
	for(int i=0,j=0;i<n;i++){
		while(j&&s[i]!=c[j]) j=pi[j-1];
		if(s[i]==c[j]) ++j;
		if(j==m){
			printf("%d\n",i-j+2);
			j=pi[m-1];
		}
	}
	for(int i=0;i<m;i++) printf("%d ",pi[i]);
	return 0;
}