manacher学习笔记

manacher算法，O(n)求最长回文子串

动态规划思想
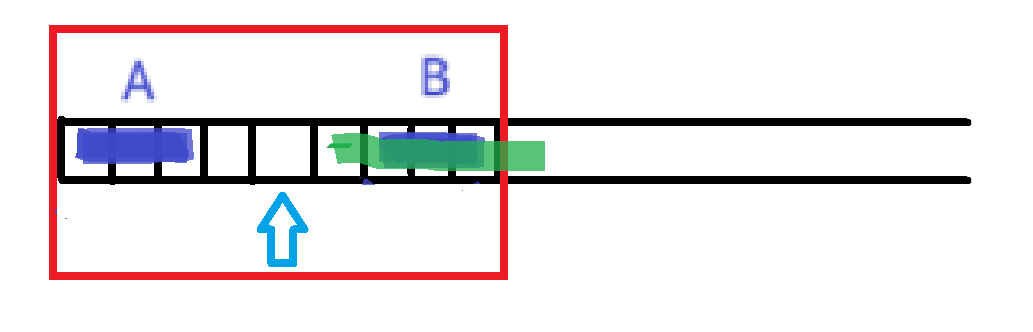
维护最长回文半径以及对应的对称点
计算新的点的回文半径时，先看它在不在最长半径内

若在，则它在该最长半径内的回文情况与它的对称点的回文点是一样的p[i] = min(p[j], mr - i + 1);
若无，则将其先设为1

然后继续向外枚举匹配并更新最长回文半径即可

为了排除偶数位的回文子串没有对称中心的缺陷
可以先初始化字符串，如

ABBAC -> $#A#B#B#A#^

CODE

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1.1e7 + 5;

int n, ans;
char a[maxn], s[maxn<<1];
int p[maxn<<1], mid, mr;

void init() {
	s[n++] = '$';
	s[n++] = '#';
	for (int i = 0; a[i]; i++) {
		s[n++] = a[i];
		s[n++] = '#';
	}
	s[n++] = '^';
}

void manacher() {
	mid = 1;
	mr = 1;
	p[1] = 1;
	for (int i = 2; i < n - 1; i++) {
		if (mr < i) p[i] = 1;
		else {
			int j = 2 * mid - i;
			p[i] = min(p[j], mr - i + 1);
		}
		while (s[i-p[i]] == s[i+p[i]])
			p[i]++;
		if (i + p[i] - 1 > mr) {
			mid = i;
			mr = i + p[i] - 1;
		}
		ans = max(ans, p[i]-1);
	}
}

int main() {
	scanf("%s", a);
	init();
	manacher();
	printf("%d\n", ans);
	return 0;
}