图

目录

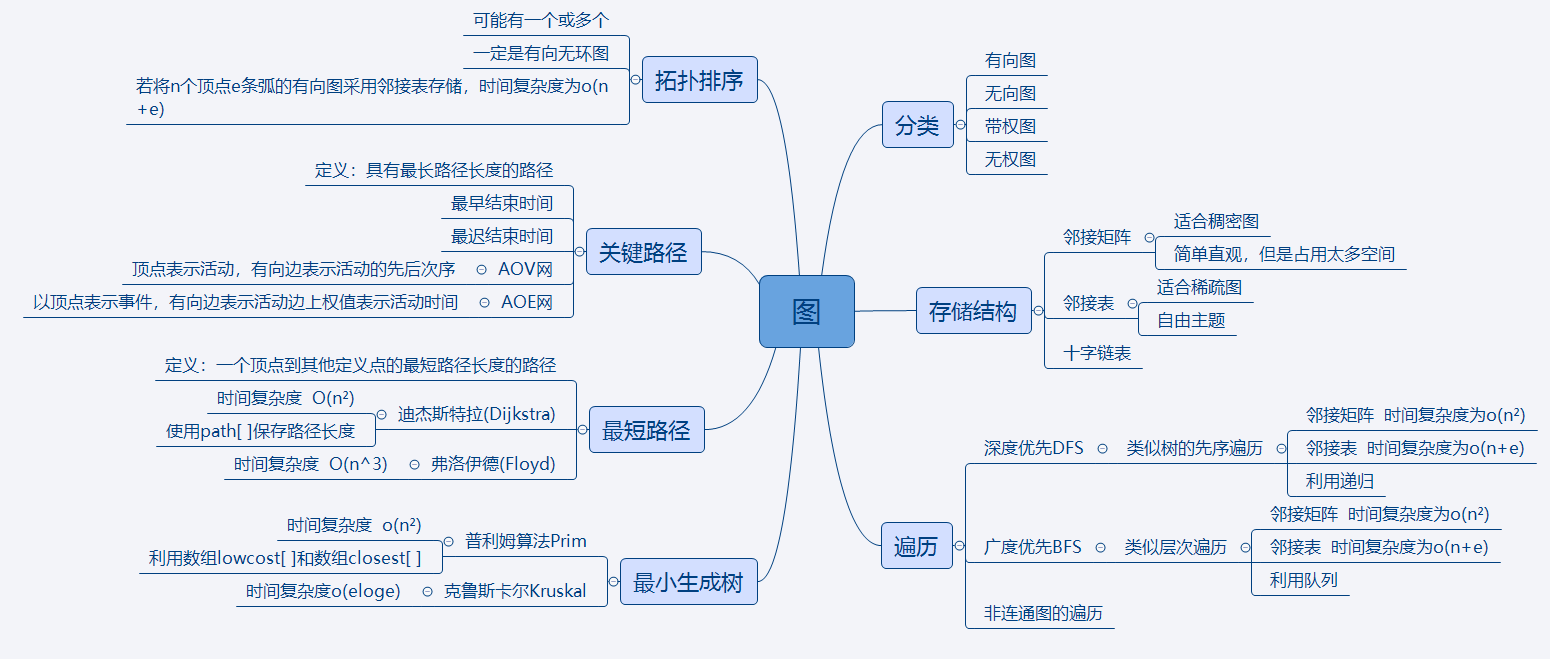
• 1.思维导图
• 2.重要概念的笔记
  • 邻接矩阵的创建、深度优先遍历、广度优先遍历
  • 邻接表的创建、深度优先遍历、广度优先遍历
  • 普利姆算法和卡鲁斯卡尔算法
  • 知识点简单总结
    • 最短路径问题
    • 关键路径
    • 拓扑排序
• 3.疑难问题及解决方案

1.思维导图

2.重要概念的笔记

邻接矩阵的创建、深度优先遍历、广度优先遍历

void CreateMGraph(MGraph& g, int n, int e)
{
	g.n = n;
	g.e = e;
	int i, j, x, y;
	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= n; j++)
			g.edges[i][j] = 0;
	}
	for (i = 0; i < e; i++)
	{
		cin >> x >> y;
		g.edges[x][y] = 1;
		g.edges[y][x] = 1;
	}
}
int h = 0;
void DFS(MGraph g, int v)
{
	if (h == 0)
	{
		h = 1;
		cout << v;
	}
	else cout << " " << v;
	visited[v] = 1;
	int i;
	for (i = 1; i <= g.n; i++)
	{
		if (!visited[i] && g.edges[v][i])
			DFS(g, i);
	}
}
#include<queue>
int l = 0;
void BFS(MGraph g, int v)
{
	queue<int>q;
	visited[v] = 1;
	q.push(v);
	int k, i;
	while (!q.empty())
	{
		k = q.front();
		for (i = 1; i <= g.n; i++)
		{
			if (visited[i] == 0 && g.edges[k][i])
			{
				q.push(i);
				visited[i] = 1;
			}
		}
		if (l == 0)
		{
			l = 1;
			cout << k;
		}
		else cout << " " << k;
		q.pop();
	}
}

邻接表的创建、深度优先遍历、广度优先遍历

void CreateAdj(AdjGraph*& G, int n, int e)
{
	G = new AdjGraph;
	G->n = n;
	G->e = e;
	int i, a, b;
	for (i = 1; i <= G->n; i++)
		G->adjlist[i].firstarc = NULL;
	for (i = 1; i <= e; i++)
	{
		cin >> a >> b;
		ArcNode* p, * q;
		p = new ArcNode;
		q = new ArcNode;
		p->adjvex = a;
		q->adjvex = b;
		p->nextarc = G->adjlist[b].firstarc;
		G->adjlist[b].firstarc = p;
		q->nextarc = G->adjlist[a].firstarc;
		G->adjlist[a].firstarc = q;
	}
}
int h = 0;
void DFS(AdjGraph* G, int v)
{
	if (h == 0)
	{
		h = 1;
		cout << v;
	}
	else cout << " " << v;
	visited[v] = 1;
	ArcNode* p;
	p = G->adjlist[v].firstarc;
	while (p != NULL)
	{
		if (visited[p->adjvex] == 0)
			DFS(G, p->adjvex);
		p = p->nextarc;
	}
}
void BFS(AdjGraph* G, int v)
{
	queue<int>q;
	ArcNode* p;
	int w;
	q.push(v);
	visited[v] = 1;
	cout << v;
	while (!q.empty())
	{
		w = q.front();
		q.pop();
		p = G->adjlist[w].firstarc;
		while (p != NULL)
		{
			if (visited[p->adjvex] == 0)
			{
				q.push(p->adjvex);
				cout << " " << p->adjvex;
				visited[p->adjvex] = 1;
			}
			p = p->nextarc;
		}
	}
}

普利姆算法和卡鲁斯卡尔算法

#define INF 32767
void Prim(MGraph g, int v)
{
	int lowcost[MAXV];
	int MIN;
	int closest[MAXV], i, j, k;
	for (i = 0; i < g.n; i++)
	{
		lowcost[i] = g.edges[v][i];
		closest[i] = v;
	}
	for (i = 1; i < g.n; i++)
	{
		MIN = INF;
		for(j=0;j<g.n;j++)
			if (lowcost[j] != 0 && lowcost[j] < MIN)
			{
				MIN = lowcost[j];
				k = j;
			}
		cout << "边 边 权值：" << closest[k] << " " << k << " " << MIN;
		lowcost[k] = 0;
		for(j=0;j<g.n;j++)
			if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j])
			{
				lowcost[j] = g.edges[k][j];
				closest[j] = k;
			}
	}
}

typedef struct
{
	int u;
	int v;
	int w;
}Edge;
void InsertSort(Edge E[], int n)
{
	int i, j;
	Edge temp;
	for (i = 1; i < n; i++)
	{
		temp = E[i];
		j = i - 1;
		while (j >= 0 && temp.w < E[j].w)
		{
			E[j + 1] = E[j];
			j--;
		}
		E[j + 1] = temp;
	}
}
void Kruskal(MGraph g)
{
	int i, j, u1, v1, s1, s2, k;
	int vset[MAXV];
	Edge E[MAXSIZE];
	k = 0;
	for(i=0;i<g.n;i++)
		for (j = 0; j < g.n; j++)
		{
			if (g.edges[i][j] != 0 && g.edges[i][j] != INF)
			{
				E[k].u = i;
				E[k].v = j;
				E[k].w = g.edges[i][j];
				k++;
			}
		}
	InsertSort(E, g.e);
	for (i = 0; i < g.n; i++)
		vset[i] = 1;
	k = 1;
	j = 0;
	while (k < g.n)
	{
		u1 = E[j].u;
		v1 = E[j].v;
		s1 = vset[u1];
		s2 = vset[v1];
		if (s1 != s2)
		{
			cout << u1, v1, E[j].w;
			k++;
			for (i = 0; i < g.n; i++)
				if (vset[i] == s2)
					vset[i] = s1;
		}
		j++;
	}
}

知识点简单总结

最短路径问题

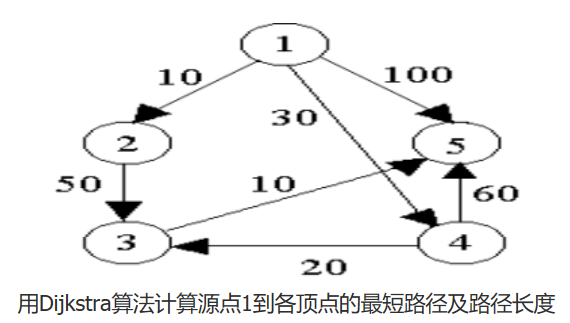
最开始只有1这个顶点，1到2、4、5距离分别为10、30、100，无法直接到3。

接着因为1、2之间权值最短，然后引入2，接着慢慢引入4、3、5。1顶点到其他顶点会随着顶点的加入可能出现更短的路径。

关键路径

关键路径就是从一个顶点到另一个顶点的最长路径

最早到达时间就是从前面开始加，最迟到达时间就是从后面开始减。

拓扑排序

前提：必须是有向无环图

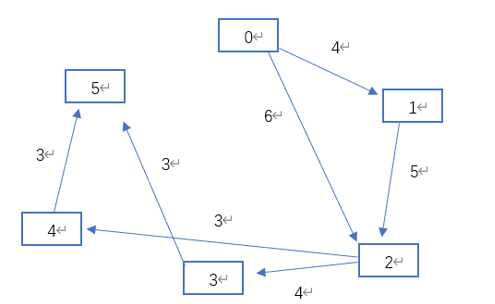
这个的方法就是没有指向它的顶点时，可以将它的顶点拿来排序，排完序后删除顶点和指向其他顶点的箭头。直到删完为止。

可以利用深度优先算法来检测是否可以拓扑排序。

3.疑难问题及解决方案

#include<iostream>
#include<string>
#include<queue>
using namespace std;

#define MAXVEXNUM 501

typedef  int ArcCell;
typedef int VexType;

typedef struct {
	VexType vexs[MAXVEXNUM];//点的集合
	VexType colors[MAXVEXNUM];//每个点对应的颜色
	ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
	int vexNum, arcNum;
}MyGraph;
int LocateVex(MyGraph& G, VexType value)
{
	for (int i = 1; i <= G.vexNum; i++)
	{
		if (value == G.vexs[i])
			return i;
	}
	return -1;
}
void CreateGraphFromConsole(MyGraph& G, int vexNum, int arcNum)
{
	G.vexNum = vexNum;
	G.arcNum = arcNum;
	for (int i = 1; i <= vexNum; i++)
	{
		for (int j = 1; j <= vexNum; j++)
		{
			G.arcs[i][j] = 0;
		}
	}
	for (int i = 1; i <= vexNum; i++)
	{
		G.vexs[i]=i;
	}
	for (int j = 1; j <= arcNum; j++)
	{
		int a, b;
		cin >> a >> b;
		G.arcs[LocateVex(G, a)][LocateVex(G, b)] = 1;
		G.arcs[LocateVex(G, b)][LocateVex(G, a)] = 1;
	}
}
int color(MyGraph& G, int K)
{
	int b[501] = { 0 }; 
	int count = 0;
	for (int k = 1; k <= G.vexNum; k++)
	{
		cin >> G.colors[k];
		b[G.colors[k]]++;
		if (b[G.colors[k]] == 1)
			count++;
	}
	if (count != K)
		return -1;
	for (int i = 1; i <= G.vexNum; i++)
	{
		for (int j = 1; j <= G.vexNum; j++)
		{
			if (G.arcs[i][j] == 1 && G.colors[i] == G.colors[j])
				return -1;
		}
	}
	return 1;
}


int main()
{
	int V, E, K, N;
	cin >> V >> E >> K;
	MyGraph G;
	CreateGraphFromConsole(G, V, E);
	cin >> N;
	int a[501], l = 0;
	for (int i = 0; i < N; i++)
	{
		a[l++] = color(G, K);
	}
	for (int i = 0; i < N; i++)
	{
		if (a[i] == 1)
			cout << "Yes" << endl;
		if (a[i] == -1)
			cout << "No" << endl;
	}
	return 0;
}

我认为这道题最大的难点是如何把建立好的图上色。

这里运用的方法是先定义一个color[ ]数组存储颜色。

用两个for循环判断if(a顶点与b顶点有边&&color[a]==color[b])则返回-1，最后输出no。