树、二叉树、查找算法总结

思维导图

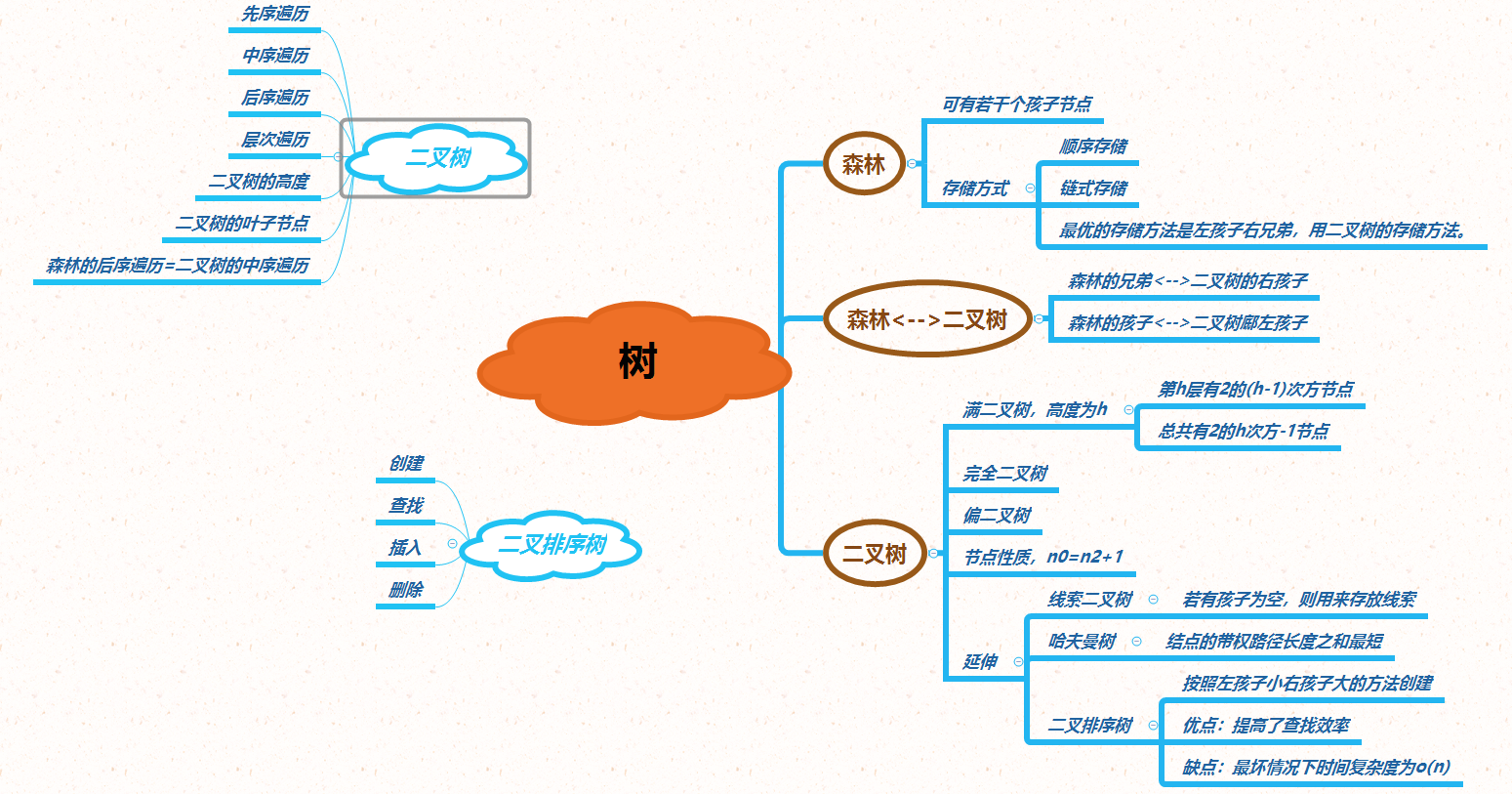
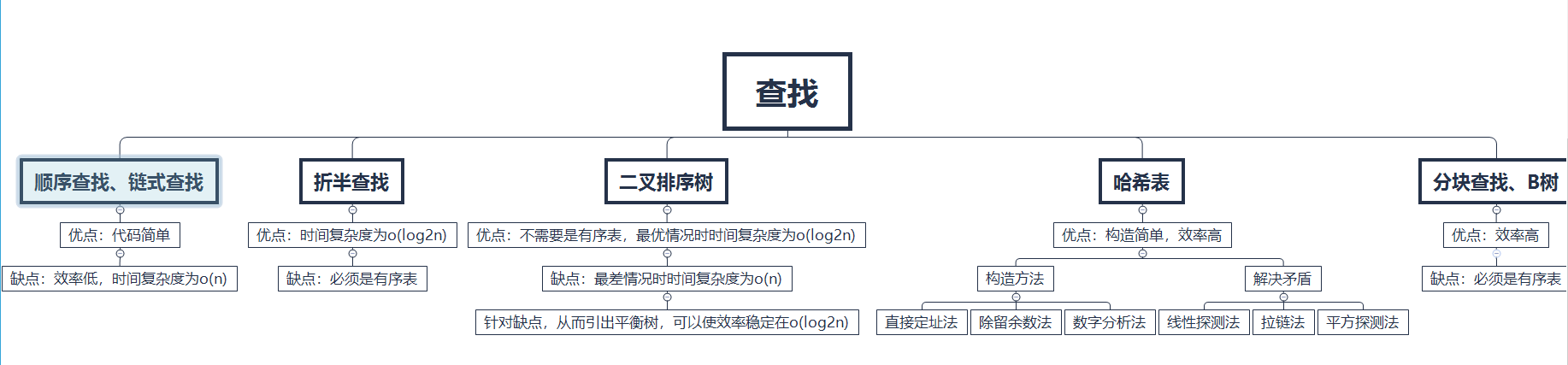
重要概念的笔记

• 前序遍历、中序遍历、后序遍历、层次遍历

  void PreOrder(BiTree T)
  {
  	if (T)
  	{
  		cout << T->data << " ";
  		PreOrder(T->lchild);
  		PreOrder(T->rchild);
  	}
  }
  void InOrder(BiTree T)
  {
  	if (T)
  	{
  		InOrder(T->lchild);
  		cout << T->data << " ";
  		InOrder(T->rchild);
  	}
  }
  void PostOrder(BiTree T)
  {
  	if (T)
  	{
  		PostOrder(T->rchild);
  		PostOrder(T->lchild);
  		cout << T->data << " ";
  	}
  }
  void LayerTraverse(BiTree T)
  {
  	queue<BiTree>q;
  	if (T == NULL)
  		return;
  	q.push(T);
  	while (!q.empty())
  	{
  		BiTree x = q.front();
  		q.pop();
  		cout << x->data;
  		if (x->lchild)
  			q.push(x->lchild);
  		if (x->rchild)
  			q.push(x->rchild);
  	}
  }
  

• 输出二叉树的高度，输出叶子节点

  int GetHeight(BiTree T)
  {
  	if (T == NULL)
  		return 0;
  	else
  	{ 
  		int lHeight = GetHeight(T->lchild);
  		int rHeight = GetHeight(T->rchild); 
  		if (lHeight > rHeight)
  			return ++lHeight;
  		else return ++rHeight;
  	}
  }
  void PreorderPrintNodes(BiTree T)
  {
  	if (T)
  	{
  		if (T->lchild == NULL && T->rchild == NULL)
  			cout << T->data << " ";
  		PreorderPrintNodes(T->lchild);
  		PreorderPrintNodes(T->rchild);
  	}
  }
  

• 二叉排序树的创建、插入、删除、查找

  BTree Creat(int n)
  {
  	BTree bt = NULL;
  	int i, x;
  	for (i = 0; i < n; i++)
  	{
  		cin >> x;
  		Insert(bt, x);
  	}
  	return bt;
  }
  int Insert(BTree &bt, keytype k)
  {
  	if (bt == NULL)
  	{
  		bt = new BTNode;
  		bt->key = k;
  		bt->rchild = NULL;
  		bt->lchild = NULL;
  		return 1;
  	}
  	else if (k == bt->key)
  		return 0;
  	else if (k > bt->key)
  		return Insert(bt->rchild, k);
  	else
  		return Insert(bt->lchild, k);
  }
  void Delete3(BTree& bt, BTree& t)
  {
  	BTree p;
  	if (t->rchild != NULL)
  		Delete3(bt, t->rchild);
  	else {
  		bt->key = t->key;
  		p = t;
  		t = t->lchild;
  		free(p);
  	}
  }
  void Delete2(BTree& bt)
  {
  	BTree p;
  	if (bt->rchild == NULL && bt->lchild == NULL)
  		bt = NULL;
  	else if (bt->rchild == NULL)
  	{
  		p = bt;
  		bt = bt->lchild;
  		free(p);
  	}
  	else if (bt->lchild == NULL)
  	{
  		p = bt;
  		bt = bt->rchild;
  		free(p);
  	}
  	else if (bt->lchild != NULL && bt->rchild != NULL)
  		Delete3(bt, bt->lchild);
  }
  int Delete1(BTree &bt,keytype k)
  {
  	if (bt == NULL)
  		return 0;
  	if (k > bt->key)
  		return Delete1(bt->rchild, k);
  	if (k < bt->key)
  		return Delete1(bt->lchild, k);
  	if (k == bt->key)
  	{
  		Delete2(bt);
  		return 1;
  	}
  }
  

• 二分法查找

  void BinSearch(SeList r,int n,KeyType k)
  {
  	int low = 0, high = n - 1, mid;
  	while (low <= high)
  	{
  		mid = (low + high) / 2;
  		if (r[mid].key == k)
  			return mid + 1;
  		if (r[mid].key > k)
  			high = mid - 1;
  		else
  			low = mid + 1;
  	}
  	return 0;
  }
  

• 线索二叉树的作用：提高查找结点与遍历二叉树的性能。

• 平衡树的作用：能够使查找效率达到稳定的o(log2n)。

• 哈夫曼树的作用：使带权路径之和最短。

• B树(三阶B树)

  1. 每个节点孩子个数不小于2
  2. 除根节点以外，其他节点最少有m/2向上取整=2个孩子
  3. 根节点有两个孩子节点
  4. 除根结点外所有节点关键字个数大于等于m/2向上取整-1=1，小于等于m-1=2
  5. 所有外部节点都在同一层上，树中总有17个关键字，外部节点有18个

疑难问题及解决方法

已解决的：平衡树达到平衡的四种情况

• RR

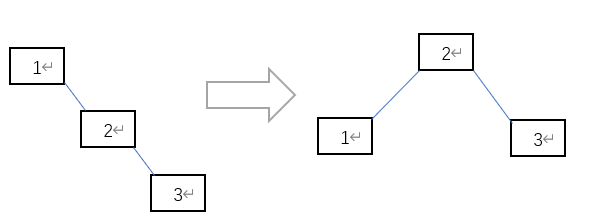
• RL

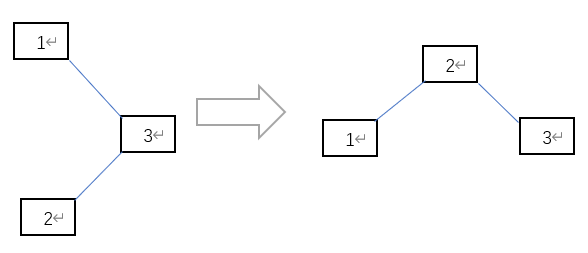
• LL

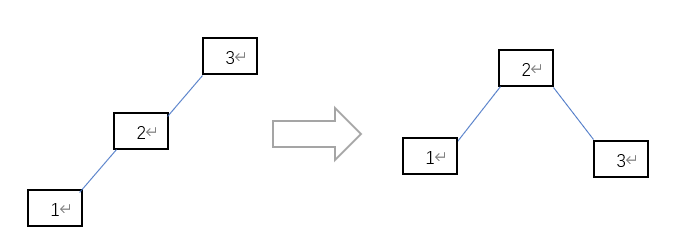
• LR

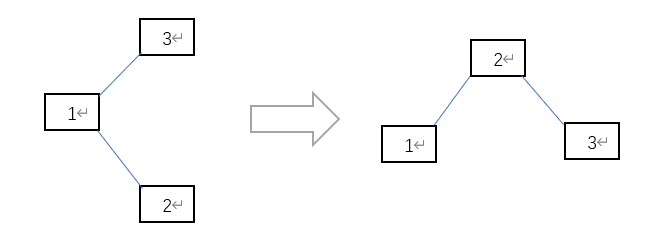
未解决的：插入时平衡树要保持平衡的算法。