二分图最大匹配——找老婆问题（确信）
定义
首先知道二分图是什么
简单的来说，就是把一个图分成两个点集，保证两个集合内部没有连边
那二分图最大匹配呢？也就是在这个图里有几条边，并且不存在多条边依附于同一个顶点（也就是一人一个老婆）
那最大的也就很显然了，就是令单身狗尽量的少
我们一般用匈牙利算法解决这一问题，说到这个就不得不提一下增广路了
增广路
定义
若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径(举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行)。
比如说我们先上一个图
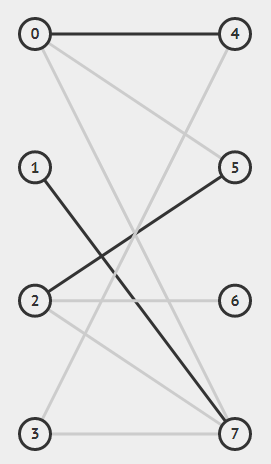
首先这里有一个M的边集{0,4 1,7 2,5}
但是我们可以找到一条增广路
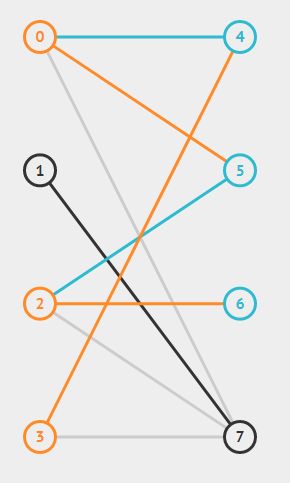
橙色即增广路，我们匈牙利算法是每次加入一个点，然后保证当前是最大二分图匹配，所以当有新的一个点（这里如3）加进来的时候，就去看它能匹配的点，（当然如果能匹配就直接匹配了）
当不能匹配的时候我们就问（能不能把你的老婆让给我？） 然后又去递归找那一个点去循环，问别人能不能让老婆，（不能让的话就等于不可以再增加最大匹配）所以我们每次都是一条尝试匹配的边（橙色的）和已经匹配的边（蓝色的）交替进行，这一条路就成为增广路——因为可以增加最大匹配的边数
性质
由增广路的定义可以推出下述五个结论:
1-P的路径长度必定为奇数，第一条边和最后一条边都不属于M。
2-不断寻找增广路可以得到一个更大的匹配M'，直到找不到更多的增广路。
3-M为G的最大匹配当且仅当不存在M的增广路径。
4-最大匹配数M+最大独立数N=总的结点数
5 -- 二分图的最小路径覆盖数 = 原图点数 - 最大匹配数
增广路主要应用于匈牙利算法中，用于求二分图最大匹配
匈牙利算法
方法
①置M为空；
②找到一条增广路径P，通过操作获得更大的匹配M'代替M；
③重复②直到找不到新的增广路径。
所以我们来看看代码（代码我是从左边连边到右边，也就是左边找老婆）
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=90010; 4 int n,m,cnt,tot,ans,tag; 5 int last[N];//链式前向星 6 bool use[N];//判断这个点是否在本次操作中有连边 7 int f[N];//右边的点和哪一个连着的（是谁的老婆 8 struct edge{ 9 int pre,to; 10 }e[N]; 11 void add(int x,int y) 12 { 13 cnt++; 14 e[cnt].pre=last[x]; 15 e[cnt].to=y; 16 last[x]=cnt; 17 } 18 bool find(int u) 19 { 20 for(int i=last[u];i;i=e[i].pre)//一条一条的找 21 { 22 int to=e[i].to; 23 if(use[to]==tag)continue;//标记这个点已经是让过得了，因为再让的话没有意义的 24 use[to]=tag;//标记 25 if(!f[to]||find(f[to]))//如果直接可以连上或者可以通过增广路得到 26 { 27 f[to]=u;//就让一让 28 return true; 29 } 30 } 31 return false; 32 } 33 int main() 34 { 35 scanf("%d%d",&n,&m); 36 for(int i=1;i<=m;i++)//连边，因为我们只需要从左边的集合走到右边的集合找老婆（你要反着来我也没意见） 37 { 38 int a,b; 39 scanf("%d%d",&a,&b); 40 add(a,b); 41 } 42 for(tag=1;tag<=n;tag++)//一个一个点加进去 43 { 44 tag++;//标记 45 if(find(tag))ans++;//能找到就多一条匹配边 46 } 47 printf("%d",ans); 48 return 0; 49 }
然后我们就有了更多的 拓 展 芝 士
最小点覆盖
即在一个图里找最少的点，并选中所连的边，使得所有的边被覆盖，这里的是二分图里的最小点覆盖
最小点覆盖=二分图最大匹配
为什么呢？
首先，光覆盖这n条匹配边，就需要n个点
然后一条最大匹配边的两端的点只能有一个点连接一个未被匹配的
如果没有，就是以下情况
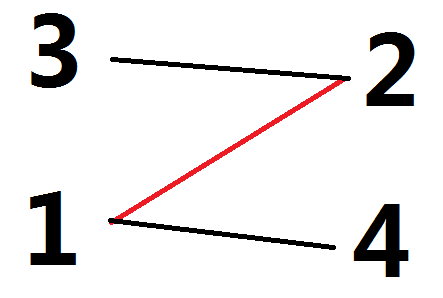
那么这就不是最大匹配了，所以不成立
所以最小点覆盖=二分图最大匹配
二分图的最大独立集
最大独立集=点数-最小点覆盖
因为选取了最小点覆盖就可以删除所有的边，所以剩下的点就是相互独立的了
最大团
就是一张图里最大的两两都有连边的
这个只在保证了取反以后可以是二分图的，因为原来是互相都相连的，所以取反后就相互独立，也就是最大独立集
最小路径覆盖
分为最小不相交路径覆盖和最小可相交路径覆盖。
小不相交路径覆盖：每一条路径经过的顶点各不相同。
最小可相交路径覆盖：每一条路径经过的顶点可以相同
DAG可相交路径
首先把每一个点拆成两个点，一个是xi，一个yi，若一个边a-b，也就是xa到by，所以就是二分图了
首先每个点都已是一个单独的路径，每次有一条边，就少了一条路径，也就是减一，所以求最大匹配即可，然后相减
