【级联失效】理解级联动力学与拓扑稳健性

网络攻击与拓扑稳健性

本文省略大量预备知识，并以极简化的方式介绍级联失效的基本概念及少量相关知识。

网络攻击

级联失效问题源于早期的网络攻击研究，目的是探索复杂网络系统功能性遭到破坏后的稳健性。最早由默奥大学的 Petter Holme 团队提出，并将网络攻击分为随机攻击和蓄意攻击两类。

Holme, Petter, et al. "Attack vulnerability of complex networks." Physical review E 65.5 (2002): 056109.

一般将被攻击的过程称为“遇袭”，网络在遇袭时，功能被逐步破坏，具体体现在移除节点或连边，导致完整的连通图裂解为无连接的小型子图。

一些研究表明，随机攻击对网络的稳健性不构成威胁，无论网络是同质性的还是异质性的，但遵循一定规则的蓄意攻击往往会对网络产生极大干扰，而且产生的影响非常依赖于网络结构本身的类型。

蓄意攻击中通过移除节点的模型一般称为点攻击（Vertex attack），以移除连边为主的模型一般称为边攻击（Edge attack），还有一种以连边信息为判断基准从而判断点是否被移除的模型，称为点边混合攻击（Vertex-Edge mix）。

点攻击往往有四种基本形式：初始度攻击（ID removal）、初始介数攻击（IB removal）（这两种方法均只使用了初始网络的信息，所以称为初始攻击策略）,重算度攻击（RD removal）、重算介数攻击（RB removal）（这两种方法在下一次攻击开始时会更新攻击策略）

D.S. Callaway, M.E.J. Newman, S.H. Strogatz, and D.J. Watts, Phys.Rev .Lett. 85, 5468 (2000).
A. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Rajagopalan, R. Stata, and J. Wiener, Computer Networks 33, 309 (2000).

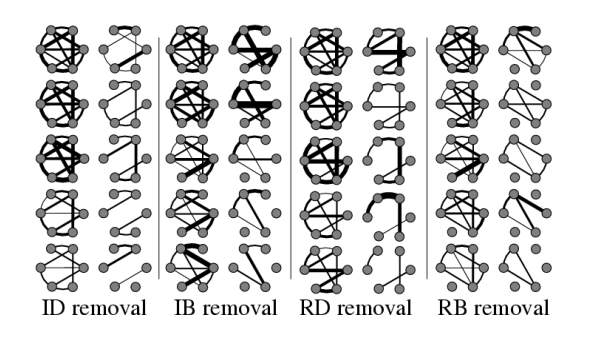
图源: Holme, Petter, et al. "Attack vulnerability of complex networks." Physical review E 65.5 (2002): 056109.

度攻击基于节点的度，通过逐步移除度较大的节点让网络功能受损。而介数攻击考虑网络中节点的介数中心性，这些节点往往可能不具有很大的度。因为两种方式对网络影响规模的不同，将基于度的攻击称为局部策略，基于介数中心性的攻击称为全局策略，前者更倾向于尽可能快的减少网络中的总边数，而后者希望尽可能破坏最短路径。

前者倾向降低总图复杂性，后者倾向裂解总图。

边攻击在模拟和计算方面比点攻击更为复杂，最典型的实例就是计算机网络集群，一般通过聚类系数可变的 Holme-Kim 无标度网络模型模拟现代计算机网络最合适。对边的攻击相当于切断通讯或网络信号。对点进行攻击的几种策略同样可以用于边攻击。由于边的度概念目前并不明确，所以定义各不相同，比如 Petter Holme 团队的研究中通过一条边连接的两节点的度乘积来衡量该边的度数。他的研究表明，采用边的介数衡量边的重要性比定义边的度数更合理。

这里简要介绍一下 Holme-Kim Scale-free 网络：
HK-scale free 网络生成算法：

1. 初始状态：网络中有 \(m_0\) 个全连通的节点

2. 衍生机制：每一时间步，一个具有 m 条边的节点 i 加入网络。节点 i 的第一条边按照度优先规则连接到网络中已存在的节点 j，即选择节点j进行连接的概率为：

\[p = \prod_j \dfrac{k_j}{\sum_{l=1}^{n}k_l} \]

3. HK机制：其余m-1条边以概率 随机连接到节点j的邻居上，否则以 的概率继续使用度优先规则。

P. Holme and B. J. Kim, "Growing scale-free networks with tunable clustering", Phys. Rev. E, 65, 026107, 2002.

Petter Holme 的研究表明，无标度网络对点攻击的敏感度远超 ER 和 SW 网络，他给出的解释是重要的 hub 节点关联着网络的大部分功能，一旦被破坏网络功能将受损严重。

拓扑稳健性

衡量网络攻击的效果如何，需要对网络结构的受损程度进行量化，也就是对拓扑稳健性进行量化。但由于网络类型繁多，指标复杂，从正面刻画破坏程度并不容易。所以目前有三种较为权威的指标用于量化网络功能的健全程度：

• 反平均最短路长度（Average inverse geodesic length）
• 最大连通子图（Largest connected subgraph）
• 损失节点比例（Loss nodes fraction）

最大连通子图在社会网络研究中又称为最大连接组件（Largest connected component）或“巨型组件”（Giant component）。

1. Average inverse geodesic length

\[l^{-1} = \left< \dfrac{1}{d(v, w)} \right> = \dfrac{1}{N(N-1) \sum_{v \in V} \sum_{w \neq v \in V} \dfrac{1}{d(v, w)'}} \]

其中 \(d(v, w)\) 表示节点 v 到节点 w 的最短路长度。

2. Largest connected subgraph
   最大连接组件即为网络中占据规模最大的连通组件。组件表示拓扑结构中两个或两个以上连通的结构。搜寻LCC的算法各不相同，互联网上有很多资料。值得注意的是，在社交网络中，蓄意攻击的预防与网络稳健性息息相关。一般社交网络的平均最短路长度与 \(\log{N}\) 成正比，且大约为 6，符合“六度分隔”理论。

S. Milgram, Psycol. Today 2, 60 (1967).

3. Loss nodes fraction

\[S = \dfrac{\sum_{i=1}^{N}s_i}{N(N-1)} \]

其中 \(s_i\) 表示第i个节点遭受攻击而导致系统中遭受连带攻击的节点数量。

社交网络这一特殊的结构还具有较高的局部传递性和高社团化，如果存在节点对 \({u, v}\), \({u, w}\), 则在社交网络中很大程度上会存在 \({v,w}\)，这样的二阶单纯性 \({u, v, w}\) 被称为“三和弦”（triad）。这种三和弦形在遇袭时有利于维持网络稳健性，比如在典型的高阶网络（high-order networks）上进行的级联过程。

C. C. Foster, A. Rapoport, and C. J. Orwant, Behavioral Science 8, 56 (1963).

蓄意攻击中最关键的意图是破坏重要的目标，一些研究表明删除网络中的重要节点，例如BA-sf 网络中的 hub 节点，会使平均最短路长度显著上升。

A.L. Barabási and R. Albert, Science 286, 509 (1999).
A.L. Barabási, R. Albert, and H. Jeong, Physica A 272, 173 (1999).

级联失效动力学

知识点摘自《集智百科》及科普视频

自组织临界与平衡态

级联故障是最近随着流量的大量增加以及系统和网络之间的高互联性而出现的。这个术语最早是在90年代末由一位荷兰的IT专业人员在这样的背景下使用的，后来慢慢成为一个形容这种大规模故障的比较常见的术语。

级联失效是一种由网络攻击所引起的大规模“雪崩”现象，当一个或多个关键节点、连边遭到破坏时，往往会将影响顺网络路径传播下去，直到引起系统彻底崩溃。要想理解级联失效背后的原因，需要对这种非线性的动力学系统进行研究。

事实上，现实中几乎任何系统均可以利用非线性的动力学方程抽象模拟（见随笔【网络重构】理解与实现基于线性模型的图重构），有的动力学系统模拟多系统交互后的转变过程，也有一些学者研究动力学系统的动态平衡，还有一些研究结合演化博弈论，为演化动力学研究提供了新的方向。

而随着对复杂系统理解的深入，人们开始对一个问题感到好奇：能否从熵增的方向逆转一个趋于稳态的复杂系统，使其最终归于混沌？

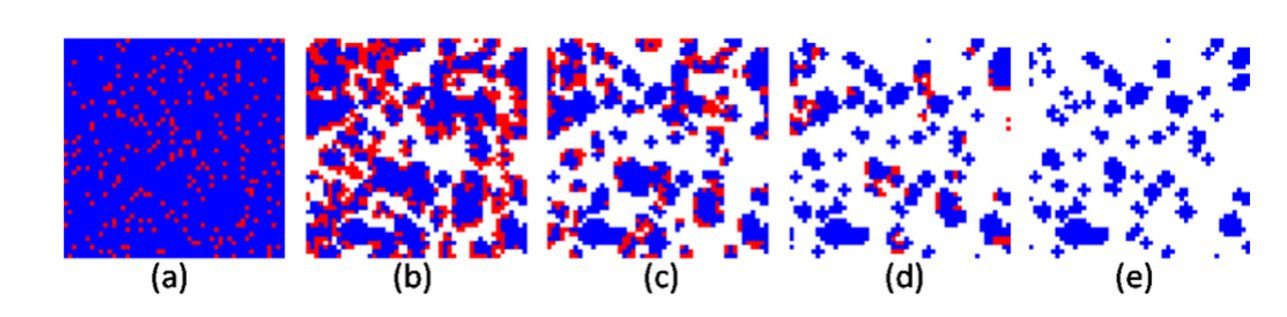
四邻居格子网络满足一定机制的级联失效自组织过程，从（a）到（e）的熵增。

图源：王文旭论文Wang, Wen-Xu, etc. "Cascading failures and the emergence of cooperation in evolutionary-game based models of social and economical networks." Chaos. 21.3 (2011): 033112.

上述问题具有十分重要的现实意义，因为相较于自然界，人类社会中的复杂系统通常处于某些条件下的相对稳定状态，而人类的进一步活动只会视为对一个平衡系统的“超额干预”，在引入外来干预的情况下，系统只能向不稳定的方向演化，最终使一个有序系统转向无序状态。例如海洋生态系统由于污染物排放而导致的食物链灾难、电力系统由于外部干扰而导致的断电、互联网系统由于黑客攻击而导致的访问错误，以及全球气候系统由于碳排放而导致的温室效应。

这样的例子不胜枚举，而解决这个基本问题有利于我们预防和阻止未来某个时点某个系统可能发生的崩溃。这个问题在21世纪的今天看来仍然是困难的。要理解一个系统如何趋于崩溃，首先我们需要了解该系统最初是如何达成稳态的。这涉及到自组织临界和平衡态过程。

（1）自组织
“组织”是一种要素有序排列以发挥功能的结构，这是一种高度抽象的概念，无法用数学语言严格定义，目前对称性理论是数学中最好的研究手段。自组织现象的术语“自组织”（self-organization）于1974年由精神病学家 W.Ross Ashby 引入现代科学，二十世纪六十年代被系统理论研究领域所广泛使用，直到上世纪七八十年代才被复杂科学研究采用。这种现象在生活中无处不在，小到人体细胞组成更为复杂的功能，雪花的规则结构，大到星系的形成。自组织现象的直观体现是有序性，那么复杂系统是如何实现有序运作的？早期研究认为是外力的介入导致系统从无序转变为有序，正如热力学第二定律表明，一个孤立系统的总熵总会随着时间的推移而增加，如果没有外部干预，一个系统不可能自发增加有序性，而代价则是降低另一个系统的稳定性（有序性），因为能量是守恒的。

而1971年诺贝尔奖得主 Llya Prigogine 对耗散结构进行的研究表明，以热力学第二定律为代表的外部干预学说可能不适合全部情形。如今更多的学者寻找自组织现象产生有序性的其他解释，并认为系统间的部分相关作用可能是影响自组织的原因之一，即协调性源于系统内部。相关研究认为系统间的非线性相关作用可以通过某种正反馈机制增强，从而产生吸引子（attractors），并创造出新的有序环境。这个过程需要系统满足远离平衡态（Far-From-Equilibrium）的条件，即对随机出现的波动和噪声足够敏感。

当系统处于远离平衡态时，它可以在有序与混沌间找到一种动态，并涌现出一些具有规律的现象。如今，学者更倾向于将这种产生现象的自组织过程称为“混沌边缘”。这种理论表明，只有当复杂系统的熵足够高的时候，才可能对其他系统微小的吸引子做出回应，并借此涌现新的现象，最后形成新的有序系统，达到某个动态平衡。

（2）混沌边缘
混沌边缘这个词最早由计算机科学家 Christopher Langton 提出，用于描述他发现的一种过渡现象，正如上述结论，当某个系统通过自组织过程，处于一个无序向有序转化的相变（Phase Transition）过程时，我们就称该系统处于混沌边缘（Edge-of-Chaos）。如果一个系统处于对称状态时，通过对称性理论和信息论，要描述一个对称系统，只需要储存一份信息而不再需要冗余信息。但如果系统间相互作用，用于自组织理论的对称性就无法映射本质上完全不同的两种系统，因此我们需要至少两个不同信息用于描述两个系统。也就是说这个两系统结构拥有更高的“统计熵”。通过这种信息论和对称性，我们就可以量化随机性和有序性，进而描述混沌边缘。

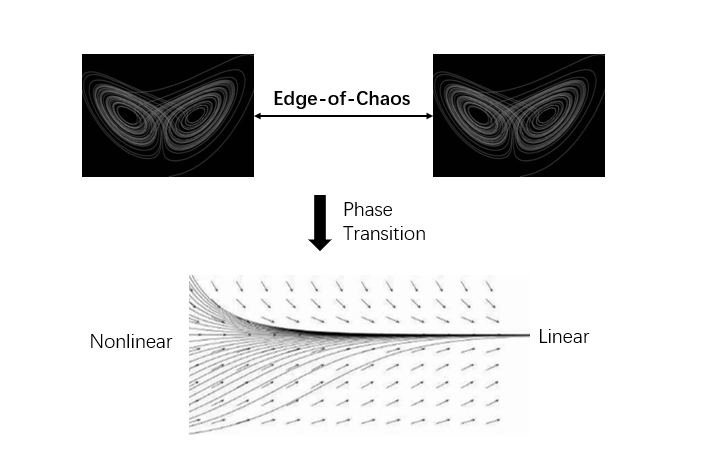
也就是说系统从混沌到有序的自组织过程可以通过一些基于信息论和物理学的转化方程描述，而这种方程一定是非线性的。因为复杂性本质上是两个及以上系统间产生的不可约的相互作用，也正因如此，复杂性一定是从系统交互的中间态中产生的。在相互作用的区域内，一些微小的波动将会更容易的被系统捕获，这些波动可以把系统带入具有吸引子的另一个系统，这个区域内产生的现象就是相变，这个区域就是混沌边缘。关于临界自组织和混沌边缘的研究目前尚存在争议。级联失效现象本质上是系统动力学的一种状态转化，而转化过程中通过攻击节点制造吸引子，可以观察系统中的临界自组织过程，类似的模型有 OPA 模型和沙堆模型，以及一些与级联过程相关的渗流模型。