2025.05.24__jyu__GDCPC训练赛1(F,G)
F题题目链接
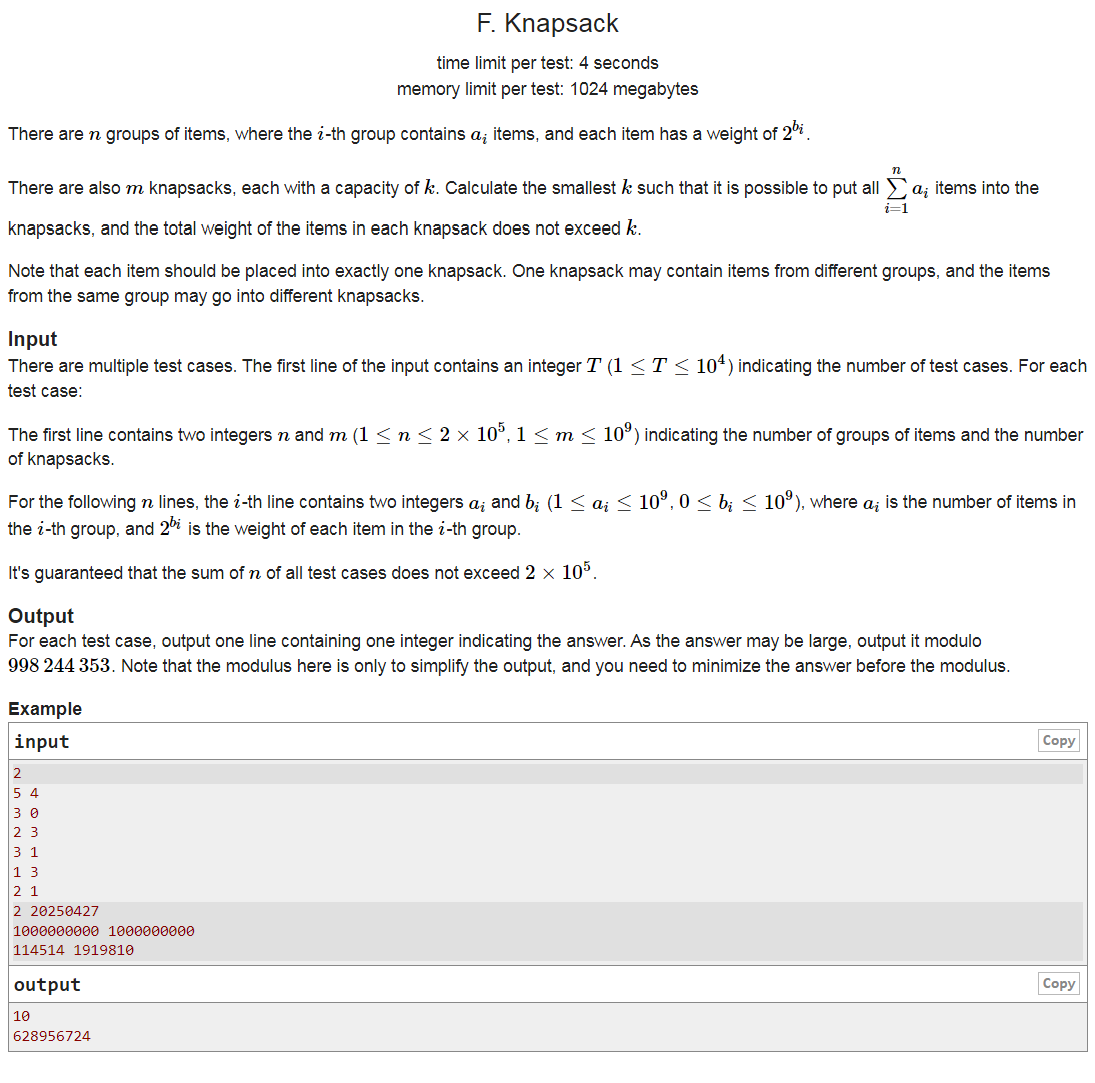
F题题目大意
给定若干a,b(a是物品数量,\(2^b\)是物品重量),用m个背包将所有物品装进去,求背包的最小容量k。
思路
容易想到,题目跟二进制有关,我们可以看成每放进一个物品,相当于在某个背包的b位加1,问最终背包的最大值的最小可以是多少。
所以他其实就是一道模拟题
按b从大到小的顺序枚举,用k记录在经过前面的操作后有多少还没填的空间,优先填k,还有剩余的话就开辟新的空间。
注意不能真算出真实的剩余空间,数值很大,存不了,我们可以记录倍数,始终让k=(未填空间)/\(2^b\),这样k就是所能填的数量。
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define LL long long
#define pb push_back
#define fi first
#define se second
#define endl '\n'
using namespace std;
const int N=1e5+10,M=1010,mod=998244353;
const int INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
int n,m,k;
int qmi(int a,int b){
int c=1;
while(b){
if(b&1) c=c*a%mod;
a=a*a%mod;
b>>=1;
}
return c;
}
int bit(int x){
int res=0;
while(x){
res++;
x>>=1;
}
return res;
}
void solve(){
cin>>n>>m;
map<int,int> mp;
for(int i=1;i<=n;i++){
int a,b;
cin>>a>>b;
mp[b]+=a;
}
vector<PII> arr;
for(auto& it:mp) arr.pb({it.fi,it.se});
sort(arr.begin(),arr.end(),greater<PII>());
int ans=0,k=0;
for(int i=0;i<arr.size();i++){
int b=arr[i].fi,a=arr[i].se;
if(i>0){
int d=arr[i-1].fi-b;
if(bit(k)+d>63&&k>0) break;
k*=1ll<<d;
}
if(k<=a){
a-=k;
int v=(a+m-1)/m;
ans=(ans+v%mod*qmi(2,b)%mod)%mod;
k=(m-a%m)%m;
}else{
k-=a;
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}
赛后总结
其实这题想明白后非常简单,模拟题罢了(虽然有一些难搞的细节),只能说我畏惧了,比赛中没去想过(捂脸)。
代码来自烁师兄,%%。
G题题目链接

G题题目大意
给定一个网格图,求从(1,1)到(n,m)的每条不同路径的元素种类数量的和。
思路
很容易想到:可以通过计算出每一个点对答案的贡献求出最终的答案。
由于题目中每一个点都有不同的数值,我们可以先把相同数值的点看成同一类型,那么最终答案就是所有类型的点的所有贡献的和。
由此,我们就可以通过算出同一类型点的总贡献进而算出所有点,这样就把问题缩小了。
那么同一类型的点的贡献怎么算呢?
很简单,就是所有经过(至少一个)该类型点的不重复路径数量。
做法
(1)用组合数去算路径数量
如果要算从(1,1)到(i,j)有多少条不同路径
从(1,1)到(i,j),需要进行i-1次向下\(\downarrow\)操作,j-1次向右\(\rightarrow\)操作,那么路径数量就相当于对这两种操作全排列的结果,也就是\(C_{i+j-2}^{i-1}\)。(相当于有i+j-2个空位,先把i-1个\(\downarrow\)填进去,剩下的空位放\(\rightarrow\))
如果要算从(1,1)经过(i,j)到达(n,m)有多少条不同路径
其实就是从(1,1)到(i,j)的路径数量乘从(i,j)到(n,m)的路径数量,也就是\(C_{i+j-2}^{i-1}\)*\(C_{n+m-i-j}^{n-i}\)。
(2)利用(1)去算同一类型的贡献
同一类型的点的所有路径中必然有一些路径会经过多个此类型点,为防止把路径多算或少算,我们可以在计算路径的时候规定:一个点的路径,从(1,1)到(i,j)是前半段,从(i,j)到(n,m)是后半段,前半段我们保证它没有经过相同类型的点,后半段允许经过同类型的点,这样就保证不会重复了。
通过(1)(2)就可以写出一种解题方法了。时间复杂度O(\(k^2\)),k为该类型有多少个点
点击查看代码
int fun1(vector<PII>& a,int c){//a存了所有数值为c的点的坐标(已从小到大排序)
int len=a.size();
vector<int> f(len,0);//f数组存从(1,1)到该点的不经过相同类型点的路径数
int res=0;
for(int i=0;i<len;i++){
f[i]=C(a[i].fi+a[i].se-2,a[i].fi-1);//先算出从(1,1)到该点的路径数,之后再去掉经过相同类型点的。
for(int j=0;j<i;j++){
if(a[j].fi<=a[i].fi&&a[j].se<=a[i].se){
f[i]=(f[i]-f[j]*C(a[i].fi+a[i].se-a[j].fi-a[j].se,a[i].fi-a[j].fi)%mod+mod)%mod;
}
}
int num=f[i]*C(n+m-a[i].fi-a[i].se,n-a[i].fi)%mod;//前半段*后半段
res=(res+num)%mod;
}
return res;
}
到此还没有终止,虽然我们已经写出了一种解题方法,但让我们分析一下时间复杂度,总共有1e5个点,枚举每一种类型都进行fun1函数,假如有10种点,每一种都有1000个,那么就是1e9的时间,会超时,寄!!!。
那么在此就要请出第二种做法——dp!!!
(3)dp求不经过某些点的路径总数
dp就是很板的dp了,经过类型点的路径数=总路径数-不经过类型点的路径数。
要算不经过类型点的路径数量,那么我们让所有类型点的dp[i][j]保持为0就可以了。
具体看代码吧,应该很好理解。
点击查看代码
int fun2(vector<vector<int>>& g,int c){//g是图
vector<vector<int>> dp(n+10,vector<int>(m+10,0));
dp[1][1]=(g[1][1]==c)?0:1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(g[i][j]==c) continue;
if(i==1&&j==1) continue;
dp[i][j]=(dp[i-1][j]+dp[i][j-1])%mod;
}
}
int res=(C(n+m-2,n-1)-dp[n][m]+mod)%mod;
return res;
}
(4)做法的选择
对于两种做法,容斥的做法(fun1)时间复杂度O(\(k^2\)),dp的做法O(nm),
nm始终不变,所以如果k<\(\sqrt{nm}\),就选fun1,否则fun2。
赛后总结
比赛的时候想到了容斥做法,俞也帮我写出了组合数的公式,但我想不出怎么去重(也就是前面的那个规定)。
dp做法也没想出来(沉默)。
感谢罗师兄的做法,在他的基础上写的这篇题解的。
全部的代码贴在这了,注释就不写全了,希望不会看不懂。
点击查看代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define LL long long
#define pb push_back
#define fi first
#define se second
#define endl '\n'
using namespace std;
const int N=1e5+10,M=1010,mod=998244353;
const int INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
int n,m,k;
int fact[N],infact[N];
int qmi(int a,int b){
int c=1;
while(b){
if(b&1) c=c*a%mod;
a=a*a%mod;
b>>=1;
}
return c;
}
void init(){
fact[0]=infact[0]=1;
for(int i=1;i<N;i++) fact[i]=fact[i-1]*i%mod;
infact[N-1]=qmi(fact[N-1],mod-2);
for(int i=N-2;i>=1;i--) infact[i]=infact[i+1]*(i+1)%mod;
}
int C(int a, int b){
if(b<0||a<b) return 0;
return fact[a]*infact[b]%mod*infact[a-b]%mod;
}
bool cmp(PII a,PII b){
if(a.first!=b.first) return a.first<b.first;
return a.second<b.second;
}
int fun1(vector<PII>& a,int c){//a存了所有数值为c的点的坐标(已从小到大排序)
int len=a.size();
vector<int> f(len,0);//f数组存从(1,1)到该点的不经过相同类型点的路径数
int res=0;
for(int i=0;i<len;i++){
f[i]=C(a[i].fi+a[i].se-2,a[i].fi-1);//先算出从(1,1)到该点的路径数,之后再去掉经过相同类型点的。
for(int j=0;j<i;j++){
if(a[j].fi<=a[i].fi&&a[j].se<=a[i].se){
f[i]=(f[i]-f[j]*C(a[i].fi+a[i].se-a[j].fi-a[j].se,a[i].fi-a[j].fi)%mod+mod)%mod;
}
}
int num=f[i]*C(n+m-a[i].fi-a[i].se,n-a[i].fi)%mod;//前半段*后半段
res=(res+num)%mod;
}
return res;
}
int fun2(vector<vector<int>>& g,int c){//g是图
vector<vector<int>> dp(n+10,vector<int>(m+10,0));
dp[1][1]=(g[1][1]==c)?0:1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(g[i][j]==c) continue;
if(i==1&&j==1) continue;
dp[i][j]=(dp[i-1][j]+dp[i][j-1])%mod;
}
}
int res=(C(n+m-2,n-1)-dp[n][m]+mod)%mod;
return res;
}
void solve(){
cin>>n>>m;
vector<vector<int>> a(n+10,vector<int>(m+10,0));
vector<vector<int>> f(n+10,vector<int>(m+10,0));
set<int> v;
map<int,vector<PII>> mp;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
v.insert(a[i][j]);
mp[a[i][j]].pb({i,j});
}
}
for(auto& it:v) sort(mp[it].begin(),mp[it].end(),cmp);
int ans=0;
int mid=sqrt(n*m);
for(auto it:v){
int x,len=mp[it].size();
if(len<=mid) x=fun1(mp[it],it);
else x=fun2(a,it);
ans=(ans+x)%mod;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
init();
int _=1;
cin>>_;
while(_--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号