2025.06.08__jyu周赛题解
A 小鱼的游泳时间(模拟)
A题题目链接
思路
将前后两个时间转化为分钟去计算,最后再转化为小时。
代码
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int a,b,c,d;
cin>>a>>b>>c>>d;
int t=c*60+d-a*60-b;
cout<<t/60<<" "<<t%60<<endl;
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
B 天使的起誓(取模运算)
B题题目链接
思路
这题的数据范围非常大,对于c++来说明显不能直接运算,python一边去。
我们要利用到取模对于加减法和乘法具有分配律的性质来做这题。
(a + b) % p = (a % p + b % p) % p
((a + b) * c) % p = ((a * c) % p + (b * c) % p) % p
举例说明:(12) % p = (10 + 2) % p = ((1 % p) * 10) % p + 2 % p;
我们可以发现对于一个数来说,它拆分成一堆数加减乘,只要有在过程中不断取余,是不会影响他最后的结果的。
所以这题的做法就是:一边读一边取模
特判:
取模答案为 0 的话,要输出模数。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
void solve(){
string s;
cin>>n>>s;
int ans=0;
for(int i=0;i<s.size();i++)
ans=(ans*10+(s[i]-'0'))%n;
if(ans) cout<<ans<<endl;
else cout<<n<<endl;
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
C 中位数(对顶堆)
C题题目链接
思路
中位数有一个性质:比中位数小的数的数量等于比中位数大的数的数量。
用这个性质我们就可以想出做法:
维护一个中位数 mid 和两个优先队列(一个小根堆,一个大根堆),小根堆 heapMin 存放比 mid 大的数,大根堆 heapMax 存放比 mid 小的数。
结构如下:
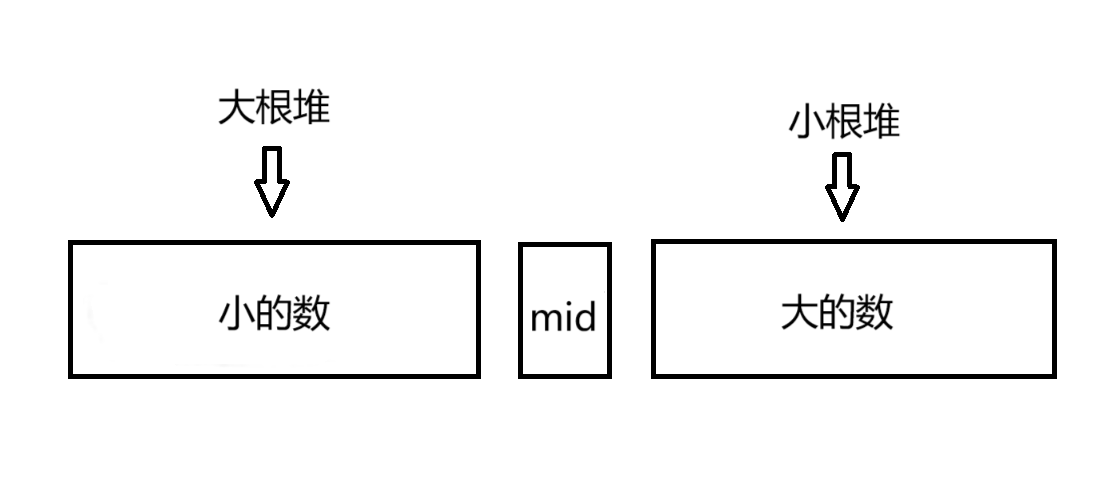
这样大根堆 heapMax 的堆顶存放的是比 mid 小的数中最大的,小根堆 heapMin 的堆顶存放的是比 mid 大的数中最小的。
输出中位数时有两种情况:
(1)两个堆的数量一样,那么显然现在的 mid 就是中位数。
(2)两个堆的数量不一样,说明此时的 mid 不是中位数。我们要做的就是把 mid 放进数量小的那个堆,再从数量大的那个堆取出一个数作为新的 mid ,直到两个堆的数量相等,那么此时的 mid 就是中位数。
代码
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
const int N=1e6+10;
int n,m,k;
int q[N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>q[i];
priority_queue<int> heapMax;
priority_queue<int,vector<int>,greater<int>> heapMin;
int mid=q[1];
cout<<mid<<endl;
for(int i=2;i<=n;i++){
if(q[i]<mid) heapMax.push(q[i]);
else heapMin.push(q[i]); //相等的数放进那个堆都可以,不影响。
if(i&1){ //相当于 i % 2 == 1 ,判断他是不是奇数个数。
while(heapMax.size()!=heapMin.size()){
if(heapMax.size()>heapMin.size()){
heapMin.push(mid);
mid=heapMax.top();
heapMax.pop();
}else{
heapMax.push(mid);
mid=heapMin.top();
heapMin.pop();
}
}
cout<<mid<<endl;
}
}
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
D 琪露诺(单调队列/优先队列优化 dp )
D题题目链接
思路
这题的思路很简单,一个点只能从 [i-l,i-r] 的点转移过来,然后希望到终点的冰冻指数最大,那么:
dp [ i ] = \(\max_{j=i-l}^{j=i-r}\) a[ j ] + a[ i ] ;
这题难的是优化,如果两重循环去写,那就是 O( \(N^2\) ) 的复杂度,理论上会超时。(虽然我第一次这么写的时候过了,沉默)
进入正题,请出单调队列/优先队列优化。
我们可以发现如果从左到右循环,那么点的转移窗口是慢慢右移的,并且由 dp 的状态转移可知,在这个窗口中我们需要关注的是是最大值,所以我们的单调队列/优先队列就是维护最大值。(优先队列就是存一下结构体就好)
代码
单调队列优化代码
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,m,k;
int q[N],dp[N],a[N];
void solve(){
int l,r;
cin>>n>>l>>r;
for(int i=0;i<=n;i++) cin>>a[i];
memset(dp,-0x3f,sizeof dp);
dp[0]=0;
int h=1,t=0,ans=-INF;
for(int i=l;i<=n;i++){
while(h<=t&&q[h]<i-r) h++;
while(h<=t&&dp[q[t]]<dp[i-l]) t--;
q[++t]=i-l;
dp[i]=dp[q[h]]+a[i];
if(i+r>n) ans=max(ans,dp[i]);
}
cout<<ans<<endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
优先队列优化代码
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,m,k;
int dp[N],a[N];
struct node{
int idx;
int num;
bool operator < (const node& u)const{
if(num!=u.num) return num<u.num;
return idx>u.idx;
}
};
void solve(){
int l,r;
cin>>n>>l>>r;
for(int i=0;i<=n;i++) cin>>a[i];
memset(dp,-0x3f,sizeof dp);
dp[0]=0;
priority_queue<node> heap;
int ans=-INF;
for(int i=l;i<=n;i++){
while(heap.size()&&heap.top().idx<i-r) heap.pop();
heap.push({i-l,dp[i-l]});
dp[i]=dp[heap.top().idx]+a[i];
if(i+r>n) ans=max(ans,dp[i]);
}
cout<<ans<<endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
E 大师(dp)
E题题目链接
思路
我们可以用 dp[ i ][ j ]表示以第 i 个为等差数列最后一个数,等差数列公差为 j 的方案数。
那么我们可以双重循环,对于第 i 个数,枚举它前面的每一个数,用这两个数构成公差来更新 dp 。
用a[ i ]、a[ j ]表示第 i 、j 个数的值,那么: dp[ i ][ a[ i ] - a[ j ] ] += dp[ j ][ a[ i ] - a[ j ] ] + 1;
(在 j 位置的每一种公差为 a[ i ] - a[ j ] 的选法方案后面加上 a[ i ] 都可以形成新的方案,再加上 a[ i ] 、a[ j ] 这两个数形成数列的方案)
最后计算每一个位置的每一种公差的和就是答案了。
tip:公差有可能为负数,为防止越界,我们可以让公差偏移一下,加上一个数,保证所有的公差都可以转成非负数,由题目数据范围可得公差最小是 \(-2*10^4\) ,那么偏移数 p 就可以定成 \(2*10^4\) 。
代码
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e6+10,MM=2020,mod=998244353;
int n,m,k;
int a[N],f[1010][40010];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
const int P=20000;
for(int i=1;i<=n;i++){
for(int j=i-1;j>0;j--){
f[i][a[i]-a[j]+P]+=(f[j][a[i]-a[j]+P]+1);
f[i][a[i]-a[j]+P]%=mod;
}
}
int ans=0;
for(int i=1;i<=n;i++)
for(int j=0;j<=2*P;j++){
ans=(ans+f[i][j])%mod;
}
cout<<ans+n<<endl;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
F Roy&October之取石子(博弈论)
F题题目链接
思路
这是一道博弈题,但我这次不打算用归纳总结的方法讲这题。很多时候我们比赛做博弈题的时候是很难直接看出它的规律,我们通常需要使用打表这一技巧。
这题我们可以使用SG函数来做。
先预处理出一定范围内的素数,然后用SG函数打表。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
#define endl '\n'
using namespace std;
const int N=1e6+10,MM=2020,mod=1e9+7;
const int INF=0x3f3f3f3f;
const int inf=0x3f3f3f3f3f3f3f3f;
int n,m,k;
bool st[N];
int prime[N],idx;
map<int,int> sg;
void getprime(int n){
for(int i=2;i<=n;i++){
if(!st[i]) prime[idx++]=i;
for(int j=0;prime[j]<=n/i;j++){
st[prime[j]*i]=true;
if(i%prime[j]==0) break;
}
}
}
int mav(set<int>& se){
for(int i=0;;i++){
if(se.find(i)==se.end()){
return i;
}
}
}
int SG(int x){
if(x==0) return 0;
if(sg[x]) return sg[x];
set<int> se;
for(int i=0;i<idx&&x>=prime[i];i++){
int y=prime[i];
while(x>=y){
se.insert(SG(x-y));
y*=prime[i];
}
}
se.insert(x-1);
return sg[x]=mav(se);
}
void table(int n){
for(int i=1;i<=n;i++){
cout<<setw(3)<<i<<" : "<<SG(i)<<" ";
// if(i%6==0) cout<<endl; //注:此处的换行是我为了等下方便展示结果的处理,实际不用写
}
}
void solve(){
int t,x;
getprime(N-10);
cin>>n;
table(n);
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}

可以很轻易地发现凡是 6 的倍数的 SG 值都为 0 ,在 SG 函数中 0 是先手必败,非 0 是先手必胜,所以我们就可以直接得到结论:如果石子数量是 6 的倍数,Roy胜,否则October胜。
这里介绍一下 SG 函数:SG 函数适用于任何公平的两人游戏, 它常被用于决定游戏的输赢结果。它通过把公平组合游戏转化成有向图,通过记忆化搜索
的优化,把一个局面的所有变化考虑到,从而得出正确的结果。
SG 函数定义必败为零,必胜为非零,如果一个点它可以转移到的状态有必胜态,那么它就是必胜态,因为当前操作者可以把局面转化成必败态给对手,反之亦然。
SG 函数还有其他更神奇的性质,在这里不一一展开,有兴趣的同学自行查找。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
void solve(){
cin>>n;
if(n%6) cout<<"October wins!"<<endl;
else cout<<"Roy wins!"<<endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号