abc416E 解题报告

abc416E 解题报告

题目

AT_abc416_e

题目分析

算法基础

首先发现, \(n \leq 500\), 有一些城市之间存在有通行时间的道路, 询问是任意两城市之间到达最短通行时间之和. 所以考虑没有修改的情况下用 Floyd 计算全源最短路, 复杂度 \(O(n^3)\), 之后 \(O(n^2)\) 求和回答询问.

添加操作的考虑

先考虑第一个操作, 对于城市 \(x\) 和 \(y\), 添加一条边的通行时间为 \(t\). 那么考虑这条边的添加, 对全源最短路中的哪些点对最短距离产生影响. 设想一下, 如果一对点的最短路不经过这条变化的边, 而且这条边变化后也不会产生更优的最短距离. 那么这对点的最短路不受影响. 反之, 最短路或变化后的最短路经过这条边的一对点受影响. 所以对于此操作, 枚举一对点 \([i, j]\), 判断这一对点经过这条新边会不会使最短路最优. 所以一次操作一造成的影响为 \(O(n^2)\).

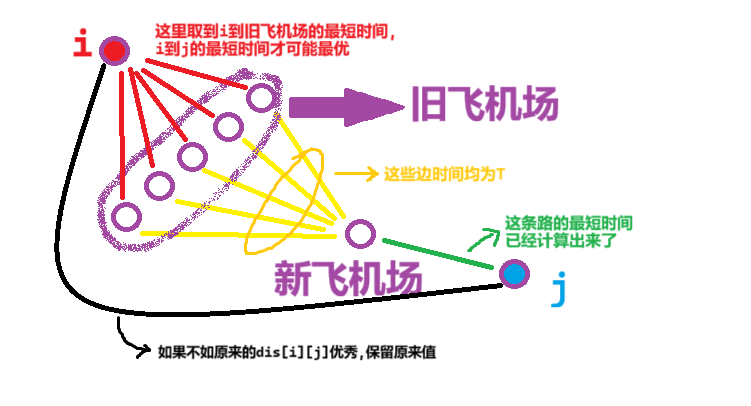
之后考虑第二个操作, 新增一个机场, 这个机场会和之前所有的机场都连时间为 \(T\) 的边. 那么这个时候的机场数为 \(O(n)\), 相当于连了 \(O(n)\) 条边, 处理一条边的复杂度为 \(O(n^2)\), 再加上 \(Q\) 次询问, 成 \(O(Q \times n^3)\), 不就炸了吗? ! 咱们将点分类抽离, 重新思考. 对于已经是飞机场的点, 要么最短路变为 \(T\), 要么不变, 这是 \(O(n)\), 非常简单. 其余不是飞机场的点, 如果最短路变优, 那么一定经过新增的航线. 再思考, 如何经过新增的航线呢? 一定是一个点 \(i\) 先到原来的机场, 然后经过新增航线到新机场, 最终到另一个点 \(j\). 而不管从哪个旧机场到新机场, 时间一定; 从新机场到 \(j\) 的最短路已经算过. 所以我们真正要维护的只是点 \(i\) 到所有旧机场的最短距离. 拥有这个最短距离的复杂度是 \(O(n^2)\). 之后对于每个 \(i\) 寻找可以更新的 \(j\), 又是 \(O(n) \times O(n)\). 成功降低了复杂度.

第二个操作如下图:

复杂度

最终复杂度: \(O(n^3 + Q \times n^2)\).

\(Code\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <set>
using namespace std;

const int NR = 510;
long long dis[NR][NR];
int d[NR];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= n; j ++)
		{
			dis[i][j] = 1e18;
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		dis[i][i] = 0;
	}
	for (int i = 1; i <= m; i ++)
	{
		int a, b;
		long long c;
		scanf("%d%d%lld", &a, &b, &c);
		dis[a][b] = dis[b][a] = min(dis[a][b], c);
	}
	int k;
	long long T;
	scanf("%d%lld", &k, &T);
	for (int i = 1; i <= k; i ++)
	{
		scanf("%d", &d[i]);
	}
	for (int i = 1; i <= k; i ++)
	{
		for (int j = 1; j <= k; j ++)
		{
			dis[d[i]][d[j]] = dis[d[j]][d[i]] = min(dis[d[i]][d[j]], T);
		}
	}
	for (int z = 1; z <= n; z ++)
	{
		for (int x = 1; x <= n; x ++)
		{
			for (int y = 1; y <= n; y ++)
			{
				dis[x][y] = min(dis[x][y], dis[x][z] + dis[z][y]);
			}
		}
	}
	int q;
	scanf("%d", &q);
	while (q --)
	{
		int opt;
		scanf("%d", &opt);
		if (opt == 1)
		{
			int x, y;
			long long t;
			scanf("%d%d%lld", &x, &y, &t);
			if (t < dis[x][y])
			{
				dis[x][y] = dis[y][x] = t;
				for (int i = 1; i <= n; i ++)
				{
					for (int j = 1; j <= n; j ++)
					{
						dis[i][j] = dis[j][i] = min(dis[i][j], dis[i][x] + t + dis[y][j]);
						dis[i][j] = dis[j][i] = min(dis[i][j], dis[i][y] + t + dis[x][j]);
					}
				}
			}
		}
		else if (opt == 2)
		{
			int x;
			scanf("%d", &x);
			for (int j = 1; j <= k; j ++)
			{
				dis[x][d[j]] = dis[d[j]][x] = min(dis[x][d[j]], T);
			}
			for (int i = 1; i <= n; i ++)
			{
				long long mn = 1e18;
				for (int j = 1; j <= k; j ++)
				{
					mn = min(mn, dis[i][d[j]]);
				}
				for (int j = 1; j <= n; j ++)
				{
					dis[i][j] = dis[j][i] = min(dis[i][j], mn + T + dis[x][j]);
				}
			}
			d[++k] = x;
		}
		else
		{
			long long ans = 0;
			for (int i = 1; i <= n; i ++)
			{
				for (int j = 1; j <= n; j ++)
				{
					if (dis[i][j] < (long long)1e18)
					{
						ans += dis[i][j];
					}
				}
			}
			printf("%lld\n", ans);
		}
	}
	return 0;
}