2025.2.8 做题记录

作业题

A - Two Arrays

开始考虑了从 \(1\) 到 \(m\) 位枚举，分别枚举 \(a\) 和 \(b\) 数组的这一位，但更新十分复杂，难以和之前的答案建立较好的联系。

老师讲解：可以使用二维前缀和优化上述过程，做到 \(O(n^3)\)

正解思路是因为 \(a_1 \leqslant a_2 \leqslant \dots \leqslant a_m\)，\(b_m \leqslant b_{m - 1} \leqslant \dots \leqslant b_1\) 且 \(a_i \leqslant b_i\)，所以 \(a_1 \leqslant a_2 \leqslant \dots \leqslant a_m \leqslant b_m \leqslant b_{m - 1} \leqslant \dots \leqslant b_1\)。只需找出长为 \(2\times m\) 的不降序列即可。

\(Code\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 1010;
const int MR = 30;
const long long mod = 1e9 + 7;
int f[MR][NR], sum[MR][NR];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int j = 1; j <= n; j ++) sum[0][j] = 1;
	for (int i = 1; i <= m * 2; i ++)
	{
		for (int j = 1; j <= n; j ++)
		{
			f[i][j] = sum[i - 1][j];
			sum[i][j] = sum[i][j - 1] + f[i][j];
			sum[i][j] %= mod;
			//cout << i << " " << j << " " << f[i][j] << " " << sum[i][j] << endl;
		}
	}
	long long ans = 0;
	for (int j = 1; j <= n; j ++)
	{
		ans += f[m * 2][j];
		ans %= mod;
	}
	printf("%lld\n", ans);
	return 0;
}

B - Writing Code

link

一开始写出来 \(O(n^4)\) 的暴力，考虑了枚举每个程序员选择几行写代码。

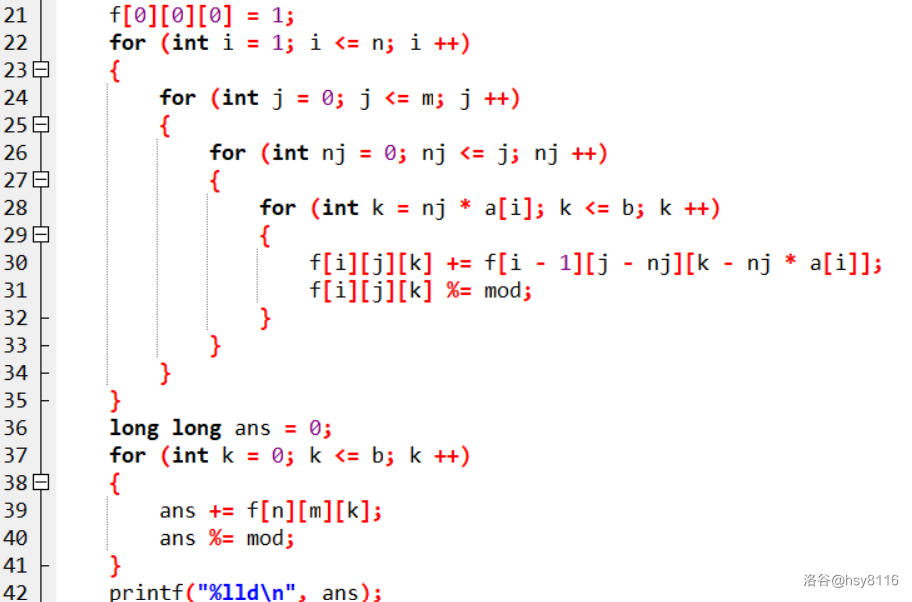
没有正确地进行模型转换，实际上这些程序员每个可以选择无数行写代码，就是一个完全背包，可以直接做了，不用枚举行数，只用去掉第一维、从小到大枚举容量（即 bug 数）。

\(\boxed{\textcolor{red}{\Large \rm 注意关注特定的模型！}}\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 510;
int a[NR];
long long f[NR][NR];

int main()
{
	int n, m, b;
	long long mod;
	scanf("%d%d%d%lld", &n, &m, &b, &mod);
	for (int i = 1; i <= n; i ++)
	{
		scanf("%d", &a[i]);
	}
	f[0][0] = 1;
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			for (int k = a[i]; k <= b; k ++)
			{
				f[j][k] += f[j - 1][k - a[i]];
				f[j][k] %= mod;
			}
		}
	}
	long long ans = 0;
	for (int k = 0; k <= b; k ++)
	{
		ans += f[m][k];
		ans %= mod;
	}
	printf("%lld\n", ans);
	return 0;
}

C - Chip Move

link

个人博客题解——更好的解释思维

最开始的暴力解法答案正确。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 4e4 + 10;
const int MR = sqrt(2 * NR);
const long long mod = 998244353;
long long f[NR][MR];

int main()
{
	int n, k;
	scanf("%d%d", &n, &k);
	f[0][0] = 1;
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= sqrt(2 * n); j ++)
		{
			if (i - (k + j - 1) < 0) break;
			for (int o = 1; ; o ++)
			{
				int l = i - o * (k + j - 1);
				if (l < 0) break;
				//cout << i << " " << l << endl;
				f[i][j] += f[l][j - 1];
				f[i][j] %= mod;
				//cout << "f " << i << " " << j << " " << f[i][j] << endl;
			}
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		long long sum = 0;
		for (int j = 1; j <= sqrt(2 * n); j ++)
		{
			sum += f[i][j];
			sum %= mod;
		}
		printf("%lld ", sum);
	}
	puts("");
	return 0;
}

后来考虑完全背包优化掉上面暴力中的 o 的遍历，改为了：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 4e4 + 10;
const int MR = sqrt(2 * NR);
const long long mod = 998244353;
long long f[NR];

int main()
{
	int n, k;
	scanf("%d%d", &n, &k);
	f[0] = 1;
	for (int j = 1; j <= sqrt(2 * n); j ++)
	{
		for (int i = 1; i <= n; i ++)
		{
			int l = i - (k + j - 1);
			if (l < 0) continue;
			//cout << i << " " << l << endl;
			f[i] += f[l];
			f[i] %= mod;
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		printf("%lld ", f[i]);
	}
	puts("");
	return 0;
}

这个代码的优点是避免了每步次数的枚举，用完全背包实现正倍数的步数行走。但是这个代码无法保证步数序号的连续性。例如，可能在走完 \(5\) 次第一步后直接去走 \(3\) 次第三步，显然不合理。

我们尝试保留第二版代码 \(O(n \sqrt{n})\) 的复杂度，同时实现步数的连续性。

考虑最坏情况下，\(k = 1\)，从 \(1\) 的步长开始走，每多一步，步长只加 \(1\)。所以 \(1 + 2 + \dots + m = n\)，\(m\) 为最多的步数。

\(\therefore \frac{(m + 1) m}{2} = n\)

\(又 \because \frac{(\sqrt{2n} + 1) \sqrt{2n}}{2} = \frac{2n + \sqrt{2n}}{2} = n + \frac{\sqrt{2n}}{2} \gt n\)

\(\therefore m \lt \sqrt{2n}\)

枚举步数复杂度 \(O(\sqrt{n})\) 枚举每个地点复杂度 \(O(n)\) 所以 \(\bf DP\) 两层循环的复杂度为 \(O(n \sqrt{n})\)。内部的复杂度要尽量小。

还是考虑使用暴力的部分思路。

f[0][0] = 1;
for (int i = 1; i <= n; i ++)
{
    for (int j = 1; j <= sqrt(2 * n); j ++)
    {
        if (i - (k + j - 1) < 0) break;
        for (int o = 1; ; o ++)
        {
            int l = i - o * (k + j - 1);
            if (l < 0) break;
            f[i][j] += f[l][j - 1];
            f[i][j] %= mod;
        }
    }
}

注意到，这里枚举的 o 费了时间复杂度。又考虑更新 i 的位置 l 和 i 位置的差都是这一步步长的倍数，因此这两个位置对步长取余的余数相等。

所以可以开一个数组 mstep 记录对步长取余余数相同的位置的方案数和，更新时，直接加上这个值即可。

也要注意更新 i 的位置 l 必须在 i 之前，所以对每个步长都要重置一下 mstep，然后按位置从小到大在计算新答案的同时将上一步这个位置的方案数放入 mstep。这样既保证遍历到后面的位置时使用的 mstep 值是之前可行的位置转移来的；又保证计算的新答案的值是由上一步得来的，不会出现跳步的情况。

在对特定步长下每个位置计算的时候，我们可以直接将这一步长的答案值存入每个位置的最终答案。

最后，如果开 \(O(n \sqrt{n})\) 的 \(\bf DP\) 数组会炸空间，所以考虑滚动数组，滚掉步数这一维。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 2e5 + 10;
const int MR = sqrt(2 * NR);
const long long mod = 998244353;
long long f[NR][2]; // f[i][j] 表示走到第 j 步，第 i 个位置的方案数，这里将 j 这维滚动
long long mstep[NR]; // 对步长取余余数相同的位置的方案数和
long long ans[NR];

int main()
{
	int n, k;
	scanf("%d%d", &n, &k);
	for (int j = 1; j <= sqrt(2 * n); j ++)
	{
		int step = (k + j - 1); // 步长
		for (int i = 0; i <= step; i ++)
		{
			mstep[i] = 0;
		}
		if (j == 1) mstep[0] = 1; // 走第一步时可从 0 走过来
		for (int i = 1; i <= n; i ++)
		{
			f[i][j % 2] = mstep[i % step];
			f[i][j % 2] %= mod;
			mstep[i % step] += f[i][(j % 2) ^ 1];
			mstep[i % step] %= mod;
			ans[i] += f[i][j % 2];
			ans[i] %= mod;
		}
	}
	for (int i = 1; i <= n; i ++)
	{
		printf("%lld ", ans[i]);
	}
	puts("");
	return 0;
}

D - Salazar Slytherin's Locket

link

看出了 \(\bf 数位 DP\)，但是不知道对不同的进制怎么处理数码的出现问题。

对每个数字出现的个数进行二进制状态压缩，\(0\) 表示出现偶数次，\(1\) 表示出现奇数次。

a clear solution —— Luogu tutorial

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 70;
const int SR = (1 << 10) + 10;
int a[NR], sz;
long long f[15][NR][SR][2];

long long digital_DP(int b, int digit, int status, int leading_zero, int reach_boundary)
{
    if (digit == 0)
    {
        return (status == 0 && leading_zero == 0);
    }
    if (reach_boundary == 0 && f[b][digit][status][leading_zero] != -1)
    {
        return f[b][digit][status][leading_zero];
    }
    long long res = 0;
    int lim = (reach_boundary) ? a[digit] : (b - 1);
    for (int i = 0; i <= lim; i ++)
    {
    	int new_status;
    	if (leading_zero && (i == 0))
    	{
    		new_status = status;
		}
		else
		{
			new_status = status ^ (1 << i);
		}
        res += digital_DP(b, digit - 1, new_status, (leading_zero && (i == 0)), (reach_boundary && (i == lim)));
    }
    if (reach_boundary == 0) f[b][digit][status][leading_zero] = res;
    return res;
}

long long solve(int b, long long x)
{
    sz = 0;
    while (x > 0)
    {
        a[++sz] = x % b;
        x /= b;
    }
    return digital_DP(b, sz, 0, 1, 1);
}

int main()
{
    memset(f, -1, sizeof(f));
    int q;
    scanf("%d", &q);
    while (q --)
    {
        int b;
        long long l, r;
        scanf("%d%lld%lld", &b, &l, &r);
        long long ans = solve(b, r) - solve(b, l - 1);
        printf("%lld\n", ans);
    }
    return 0;
}

关注以下代码：

错误

正确1

正确2

注意：在 \(\bf 数位 DP\) 的数组记录中，不能记录顶上界的状态，记录了就会错误；可以记录前导 \(0\) 的状态，实现时间复杂度的优化，例如正确2优于正确1。

证明：举出 \(1 \ 2 \ 3 \ 4\) 和 \(1 \ 2 \ 5 \ 6\) 的例子，如果在 \(2\) 这位记录顶界情况，那么两个数之后的答案不同，造成计算时的混用。

posted @ 2025-02-08 17:14 hsy8116 阅读(4) 评论(0) 收藏举报

刷新页面返回顶部

hsy8116

2025.2.8 做题记录

作业题

A - Two Arrays

B - Writing Code

C - Chip Move

D - Salazar Slytherin's Locket

公告