分块笔记
分块笔记
NFLS-S-分块的应用 2024.11.2
分块的概念
设将 \(n\) 个元素分成块长为 \(S\) 的几块,那么完整块的数量为 \(n \div S\),不完整的块需要扫描长最大为 \(S\)。
复杂度 \(O(S + n \div S)\)。
\(1 \ 2 \ 3 \ 4 \ 5 \ 6 \ 7 \ 8 \ 9 \ 10 \ 11 \ 12 \ 13 \ 14 \ 15 \ 16\\ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1 \ 2 \ 2 \ 2 \ \ \ 2 \ \ \ 3 \ \ \ 3 \ \ \ 3 \ \ \ 3 \ \ \ 4\)
分块代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int NR = 1e5 + 500;
const int SR = 320;
int S;
long long a[NR], b[SR], add[SR];
int lid[SR], rid[SR], bid[NR];
void down(int k)
{
if (add[k] == 0) return;
for (int i = lid[k]; i <= rid[k]; i ++)
{
a[i] += add[k];
b[k] += add[k];
}
add[k] = 0;
}
long long query(int l, int r)
{
int kl = l / S, kr = r / S;
long long res = 0;
if (kl == kr)
{
down(kl);
for (int i = l; i <= r; i ++)
{
res += a[i];
}
return res;
}
down(kl);
for (int i = l; i < (kl + 1) * S; i ++)
{
res += a[i];
}
down(kr);
for (int i = kr * S; i <= r; i ++)
{
res += a[i];
}
for (int i = kl + 1; i < kr; i ++)
{
res += b[i] + add[i] * S;
}
return res;
}
void modify(int l, int r, long long val)
{
int kl = l / S, kr = r / S;
if (kl == kr)
{
for (int i = l; i <= r; i ++)
{
a[i] += val;
b[kl] += val;
}
return;
}
for (int i = l; i < (kl + 1) * S; i ++)
{
a[i] += val;
b[kl] += val;
}
for (int i = kr * S; i <= r; i ++)
{
a[i] += val;
b[kr] += val;
}
for (int i = kl + 1; i < kr; i ++)
{
add[i] += val;
}
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
S = sqrt(n);
for (int i = 1; i <= n; i ++)
{
scanf("%lld", &a[i]);
int k = i / S;
b[k] += a[i];
if (lid[k] == 0) lid[k] = i;
rid[k] = i;
bid[i] = k;
}
char s[10];
int x, y, z;
while (m --)
{
scanf(" %s %d %d", &s, &x, &y);
if (s[0] == 'Q') printf("%lld\n", query(x, y));
else
{
scanf("%d", &z);
modify(x, y, z);
}
}
return 0;
}
例题
C.刷漆升级
题面
题目描述
这次的刷漆问题升级啦。 有编号为 \(0\) 到 \(n-1\) 的 \(n\) 面墙,操作是每次把连续编号的一段墙刷成 \(c\) 颜色,询问是问某段有多少面墙的颜色是 \(c\)。
输入格式
第一行两个整数 \(n\) 和 \(m\)。
第二行 \(n\) 个整数,表示每面墙初始的颜色。
接下里 \(m\) 行,每行属于下列一种:
1 a b c:把编号 \([a,b]\) 的墙刷成c颜色。
2 a b c:询问编号 \([a,b]\) 有多少面墙的颜色是 \(c\)。
输出格式
对于每个询问输出相应的结果。
样例
输入
5 5
1 2 3 4 0
2 1 3 3
1 1 3 1
2 1 3 3
2 0 3 1
2 3 4 1
输出
1
0
4
1
数据范围
\(n,m \isin [1, 10^5]; \\ 0 \leq a \leq b \leq n-1; \\ c \isin [0, 2^{31}).\)
解题
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
#include <unordered_map>
using namespace std;
const int NR = 1e5 + 10;
const int SR = 320;
int a[NR];
int S;
unordered_map<int, int> b[SR];
int lid[SR], rid[SR], bid[NR];
int tag[SR];
void down(int k)
{
if (tag[k] == -1) return;
for (int i = lid[k]; i <= rid[k]; i ++)
{
a[i] = tag[k];
}
tag[k] = -1;
}
void modify(int l, int r, int c)
{
int kl = l / S, kr = r / S;
if (kl == kr)
{
down(kl);
for (int i = l; i <= r; i ++)
{
b[kl][a[i]] --;
b[kl][c] ++;
a[i] = c;
}
return;
}
down(kl);
for (int i = l; i < S * (kl + 1); i ++)
{
b[kl][a[i]] --;
b[kl][c] ++;
a[i] = c;
}
down(kr);
for (int i = S * kr; i <= r; i ++)
{
b[kr][a[i]] --;
b[kr][c] ++;
a[i] = c;
}
for (int i = kl + 1; i < kr; i ++)
{
tag[i] = c;
b[i].clear();
b[i][c] = rid[i] - lid[i] + 1;
}
}
int query(int l, int r, int c)
{
int kl = l / S, kr = r / S;
int res = 0;
if (kl == kr)
{
down(kl);
for (int i = l; i <= r; i ++)
{
if (a[i] == c) res ++;
}
return res;
}
down(kl);
for (int i = l; i < S * (kl + 1); i ++)
{
if (a[i] == c) res ++;
}
down(kr);
for (int i = S * kr; i <= r; i ++)
{
if (a[i] == c) res ++;
}
for (int i = kl + 1; i < kr; i ++)
{
res += b[i][c];
}
return res;
}
int main()
{
memset(tag, -1, sizeof(tag));
int n, m;
scanf("%d%d", &n, &m);
S = sqrt(n);
for (int i = 1; i <= n; i ++)
{
scanf("%d", &a[i]);
int k = i / S;
b[k][a[i]] ++;
if (lid[k] == 0) lid[k] = i;
rid[k] = i;
bid[i] = k;
}
while (m --)
{
int op, x, y, z;
scanf("%d%d%d%d", &op, &x, &y, &z);
x ++;
y ++;
if (op == 1)
{
modify(x, y, z);
}
else
{
printf("%d\n", query(x, y, z));
}
}
return 0;
}
\(\textcolor{red}{注意:更新散块时,可能因为这个散块所在的全块本来有tag而出错,所以应先down(k)}\)
\(\textcolor{orange}{Code \ pieces}\)
void modify(int l, int r, int c)
{
int kl = l / S, kr = r / S;
if (kl == kr)
{
/**/down(kl);
for (int i = l; i <= r; i ++)
{
b[kl][a[i]] --;
b[kl][c] ++;
a[i] = c;
}
return;
}
/**/down(kl);
for (int i = l; i < S * (kl + 1); i ++)
{
b[kl][a[i]] --;
b[kl][c] ++;
a[i] = c;
}
/**/down(kr);
for (int i = S * kr; i <= r; i ++)
{
b[kr][a[i]] --;
b[kr][c] ++;
a[i] = c;
}
for (int i = kl + 1; i < kr; i ++)
{
tag[i] = c;
b[i].clear();
b[i][c] = rid[i] - lid[i] + 1;
}
}
最终复杂度 \(O(S \times \log_2n + \frac{n}{S} \times log_2n)\)。
D. 动态逆序对
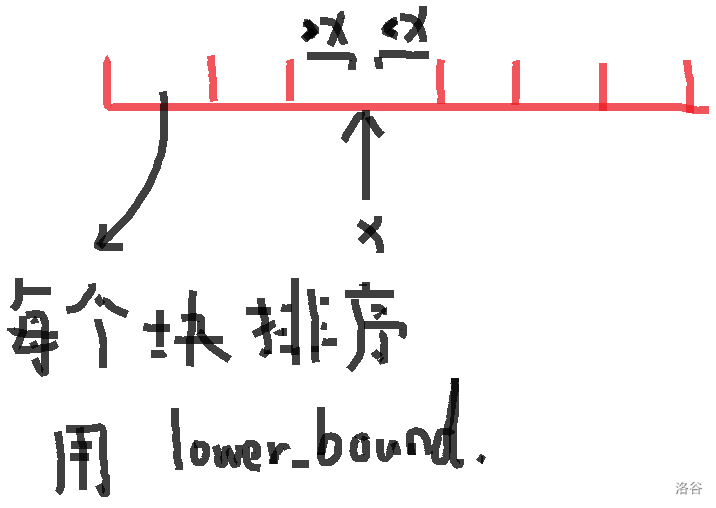
\(\Large Code\)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
using namespace std;
const int NR = 1e5 + 10;
const int SR = 320;
int S;
struct Block
{
vector<int> a;
int l, r, sz;
void bsort()
{
sort(a.begin(), a.end());
}
};
int a[NR];
Block b[SR];
int aid[NR], bid[NR];
int aa[NR], bb[NR];
int vis[NR];
long long ans = 0;
int n, m;
void merge_sort(int l, int r)
{
if (l == r) return;
int mid = (l + r) / 2;
merge_sort(l, mid);
merge_sort(mid + 1, r);
for (int i = l; i <= r; i ++)
{
bb[i] = aa[i];
}
int i = l, j = mid + 1;
int cnt = l - 1;
while (i <= mid && j <= r)
{
if (bb[i] <= bb[j])
{
aa[++cnt] = bb[i];
i ++;
}
else
{
aa[++cnt] = bb[j];
j ++;
ans += mid - i + 1;
}
}
while (i <= mid)
{
aa[++cnt] = bb[i];
i ++;
}
while (j <= r)
{
aa[++cnt] = bb[j];
j ++;
}
}
long long del(int x)
{
//cout << "_________________________________________________\nin delete\n";
//cout << x << endl;
int k = bid[x];
int l = b[k].l, r = b[k].r;
//cout << l << " " << r << endl;
int pos = aid[x];
//cout << "pos : " << pos << endl;
long long res = 0;
for (int i = l; i < pos; i ++)
{
if (vis[i]) continue;
if (a[i] > a[pos]) res ++;
}
//cout << "after a[l ~ pos - 1] : " << res << endl;
for (int i = pos + 1; i <= r; i ++)
{
if (vis[i]) continue;
if (a[i] < a[pos]) res ++;
}
//cout << "after a[pos + 1 ~ r] : " << res << endl;
for (int i = 0; i < k; i ++)
{
res += b[i].a.end() - upper_bound(b[i].a.begin(), b[i].a.end(), x);
}
//cout << "after b[1 ~ k - 1] : " << res << endl;
for (int i = k + 1; i <= n / S; i ++)
{
res += lower_bound(b[i].a.begin(), b[i].a.end(), x) - b[i].a.begin();
}
//cout << "after b[k + 1 ~ n / S] : " << res << endl;
b[k].a.erase(remove(b[k].a.begin(), b[k].a.end(), x), b[k].a.end());
b[k].sz --;
vis[pos] = 1;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
S = sqrt(n);
for (int i = 1; i <= n; i ++)
{
scanf("%d", &a[i]);
vis[i] = 0;
aa[i] = a[i];
int k = i / S;
b[k].sz ++;
b[k].a.push_back(a[i]);
if (b[k].l == 0) b[k].l = i;
b[k].r = i;
bid[a[i]] = k;
aid[a[i]] = i;
}
for (int i = 0; i <= n / S; i ++)
{
b[i].bsort();
}
merge_sort(1, n);
printf("%lld\n", ans);
while (m --)
{
int x;
scanf("%d", &x);
int dele = del(x);
ans -= dele;
//cout << dele << endl;
if (m > 0) printf("%lld\n", ans);
}
return 0;
}
\(\Large \textcolor{red}{注意:块的编号从0开始!!!开 \ long \ long !!!}\)
E. 作业
题面
题目描述
1:在人物集合 \(S\) 中加入一个新的程序员,其代号为 \(X\),保证 \(X\) 在当前集合中不存在。
2:在当前的人物集合中询问程序员的 \(\bmod Y\) 最小的值。
输入格式
第一行为用空格隔开的一个个正整数 \(N\)。
接下来有 \(N\) 行,若该行第一个字符为 A ,则表示操作 1;若为 B,表示操作 2;
数据范围
其中 对于 \(100\%\) 的数据:\(N \leq 100000\),\(1 \leq X,Y \leq 300000\),保证第二行为操作 1。
输出格式
对于操作 2,每行输出一个合法答案。
样例
样例输入
5
A 3
A 5
B 6
A 9
B 4
样例输出
3
1
样例说明
在第三行的操作前,集合里有 \(3\)、\(5\) 两个代号,此时 \(\bmod 6\) 最小的值是 \(3 \bmod 6 = 3\);
在第五行的操作前,集合里有 \(3\)、\(5\)、\(9\),此时 \(\bmod 4\) 最小的值是 \(5 \bmod 4 = 1\)。
解题
首先设 \(M\) 为 \(X, Y\) 的最大值。
-
当 \(Y \leq \sqrt{M}\) 时,对每个输入的数算 \(\bmod Y\) 的余数,并取最小值,求答案时直接得到结果,\(N \times \sqrt{M} \leq 10^{5} \times \sqrt{3 \times 10^{5}} = 5.48 \times 10^{7}\),可以处理。
-
当 \(Y \geq \sqrt{M}\) 时,存下输入的数,求答案时在 \(X\) 序列中从 \(0\) 开始到 \(M\) 每次跳跃 \(Y\) 的长度,最多跳 \(\sqrt{M}\) 次,\(N \times \sqrt{M} \leq 10^{5} \times \sqrt{3 \times 10^{5}} = 5.48 \times 10^{7}\),也可以处理。
所以考虑 \(\Large \textcolor{red}{根号分治}\)。
-
每次输入一个 \(X\) 时,对 \(1 \leq Y \leq \sqrt{M}\) 进行预处理,同时将 \(X\) 存入一个
set。 -
每次查询时,\(1 \leq Y \leq \sqrt{M}\) 的结果已经预处理,直接输出;\(Y \geq \sqrt{M}\) 的情况就在
set上做跳跃,算出答案。
\(\Large Code\)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <set>
using namespace std;
const int NR = 3e5 + 10;
const int SR = sqrt(NR);
int pans[SR + 10];
set<int> s;
int main()
{
memset(pans, 0x3f, sizeof(pans));
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
{
char op;
int x;
scanf(" %c%d", &op, &x);
if (op == 'A')
{
s.insert(x);
for (int j = 1; j <= SR; j ++)
{
pans[j] = min(pans[j], x % j);
}
}
else
{
if (x <= SR)
{
printf("%d\n", pans[x]);
}
else
{
int sans = 1e9;
for (int j = 0; j <= NR; j += x)
{
auto it = s.lower_bound(j);
if (it != s.end())
{
sans = min(sans, *it - j);
}
}
printf("%d\n", sans);
}
}
}
return 0;
}
F. Lucky
题意
题目描述
给定两个区间 \([l_i, r_i]\) 和 \([u_i, v_i]\),你可以从 \([l_i, r_i]\) 里选择一个数 \(x\),\([u_i, v_i]\)里选择一个数 \(y\),问组合 \((x, y)\) 有多少种满足 \(a_x + a_y = k\)。
输入格式
多组测试数据,一直读直到读不到输入 \(n\) 为止。
对于每组测试数据:
第一行一个整数 \(n\);第二行一个整数 \(k\),代表 WLD 的幸运数字,保证 \(k\) 为奇数。
第三行 \(n\) 个整数,表示 \(a_1, a_2, \dots , a_n\)。
第四行一个整数 \(m\),代表询问次数。
之后 \(m\) 行,每行4个整数 \(l_i, r_i, u_i, v_i\),代表一次询问。
输出格式
对于每组测试数据里的每个询问,输出一行一个整数代表其答案。
样例
输入
5
3
1 2 1 2 3
1
1 2 3 5
输出
2
数据范围
解题
考虑将一维数组转换为二维分块数组。
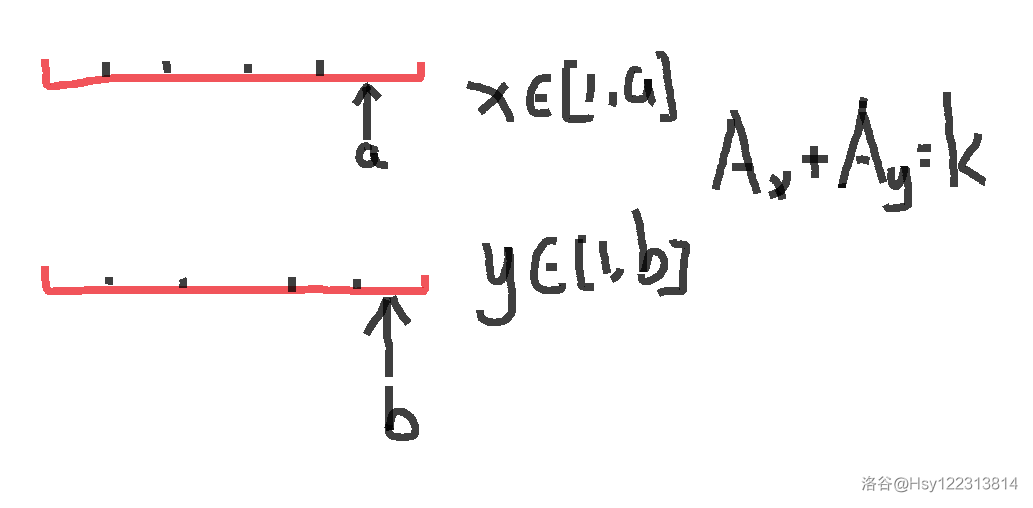
整块的很好处理,注意后面无用的散块需要去掉,具体来说,用 \(a\) 的散块配 \(b\) 一整串,用 \(b\) 的散块配 \(a\) 一整串。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int NR = 3e4 + 10;
const int SR = sqrt(NR);
int n, m;
int a[NR], g[SR][NR], f[SR][SR];
int h[NR];
int S;
int query(int x, int y)
{
int ans = f[x / S][y / S];
for (int i = x + 1; i < (x / S + 1) * S; i ++)
{
if (0 <= m - a[i] && m - a[i] <= n)
{
ans -= g[y / S][m - a[i]];
}
h[a[i]] ++;
}
for (int i = y + 1; i < (y / S + 1) * S; i ++)
{
if (0 <= m - a[i] && m - a[i] <= n)
{
ans -= g[x / S][m - a[i]] - h[m - a[i]];
}
}
for (int i = x + 1; i < (x / S + 1) * S; i ++)
{
h[a[i]] --;
}
return ans;
}
int main()
{
while (scanf("%d%d", &n, &m) != EOF)
{
S = sqrt(n);
memset(a, 0, sizeof(a));
memset(g, 0, sizeof(g));
memset(f, 0, sizeof(f));
for (int i = 1; i <= n; i ++)
{
scanf("%d", &a[i]);
}
for (int i = 0; i <= n / S; i ++)
{
for (int j = i * S; j < (i + 1) * S; j ++)
{
g[i][a[j]] ++;
}
memcpy(g[i + 1], g[i], sizeof(g[i]));
}
for (int i = 0; i <= n / S; i ++)
{
for (int j = 0; j <= n / S; j ++)
{
for (int k = j * S; k < (j + 1) * S; k ++)
{
if (0 <= m - a[k] && m - a[k] <= n)
{
f[i][j] += g[i][m - a[k]];
}
}
f[i][j + 1] = f[i][j];
}
}
int m;
scanf("%d", &m);
while (m --)
{
int l, r, u, v;
scanf("%d%d%d%d", &l, &r, &u, &v);
printf("%d\n", query(r, v) - query(l - 1, v) - query(r, u - 1) + query(l - 1, u - 1));
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号