洛谷题解：CF375B Maximum Submatrix 2

题意简述

给定一个只包含 \(01\) 的矩阵，如果可以无数次交换任意两行，求一个只包含 \(1\) 的子矩阵且满足面积最大，最大面积是多少？

思路分析

考虑到矩形的边一定是横平竖直的，所以先尝试确定下矩形的一边。图 1 中，如使 \(j=2\) 为矩形的一边，标定为 \(\textcolor{red}{红色}\)，来分析怎样计算交换后的最大矩形面积。

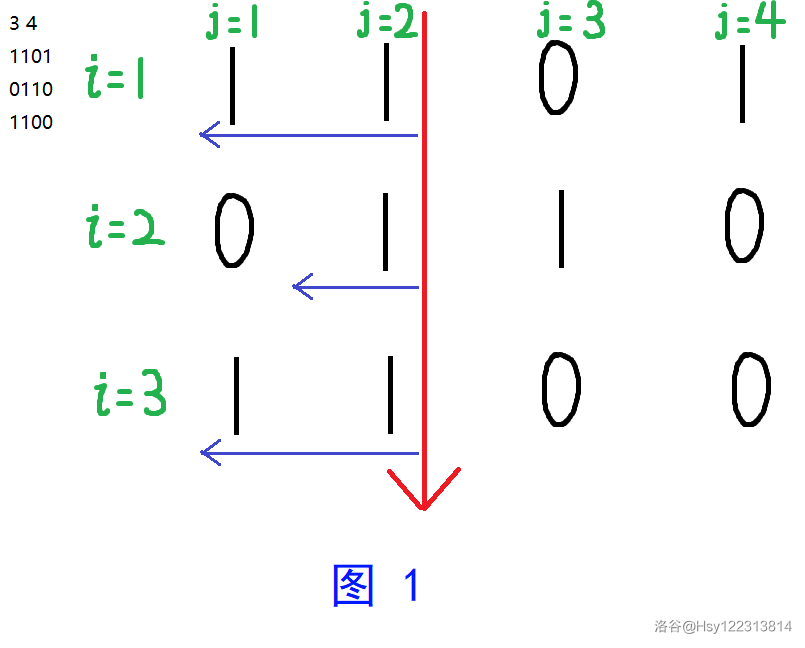
首先，在 \(j=2\) 左侧的数字中只有最右侧的连续一段的 \(1\) 才有可能记成以 \(j=2\) 为边的矩形的组成部分。这部分是我们计算要使用的，标定为 \(\textcolor{blue}{蓝色}\)，可以考虑预处理出 \(c_{i,j}\) 表示坐标 \((i,j)\) 左侧连续 \(1\) 的个数。

接下来，我们考虑 无数次交换任意两行 这个操作，如果每两行都可以无限交换，那么这个矩阵可以随意改变行的先后顺序，也就是按照一定顺序对行排序。

想到这点后，我们思考如何排序有利于矩形面积的计算。显然，当对同一列的 \(c_{i,j}\) 从小到大排序时，对于每个第 \(j\) 列第 \(i\) 行的 \(c_{i,j}\) 值 ，它对后面更大的 \(c_{i',j}\) 值的位置有贡献，这里 \(i'\) 一定在 \(i\) 后面，因而 \(c_{i,j} \leqslant c_{i',j}\)，所以 \(i\) 一定能和 \(i'\) 形成矩形，这个矩形中 \(c_{i,j}\) 就是矩形的宽，\(i’-i+1\) 就是矩形的长。很明显，\(i'\) 越大矩形的长越大，矩形的宽又不变，矩形的面积就最大，于是 \(i'\) 最优值取 \(n\) 。

总结上一段，我们对列 \(j\) 的 \(c\) 值从小到大排序，依次遍历行 \(i\)，矩形最大面积不断和 \(c_{i,j} \times (n-i+1)\) 取最大值，即可得到答案。

上图图 1 处理后形成一下图：

注意：下图中的 \(i\) 本应不改变，但为了识别不同的行在什么位置，我手动将它改变，上文中的 \(i\) 和 \(i'\) 与下图中的 \(i\) 无关。

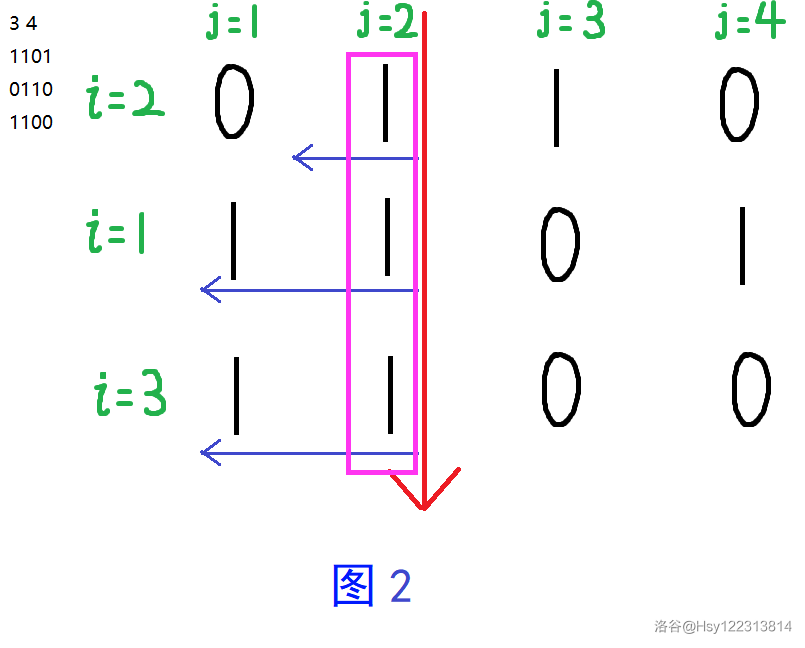
图 2 中考虑第 \(1\) 行时，最大矩形面积为 \(3\)。

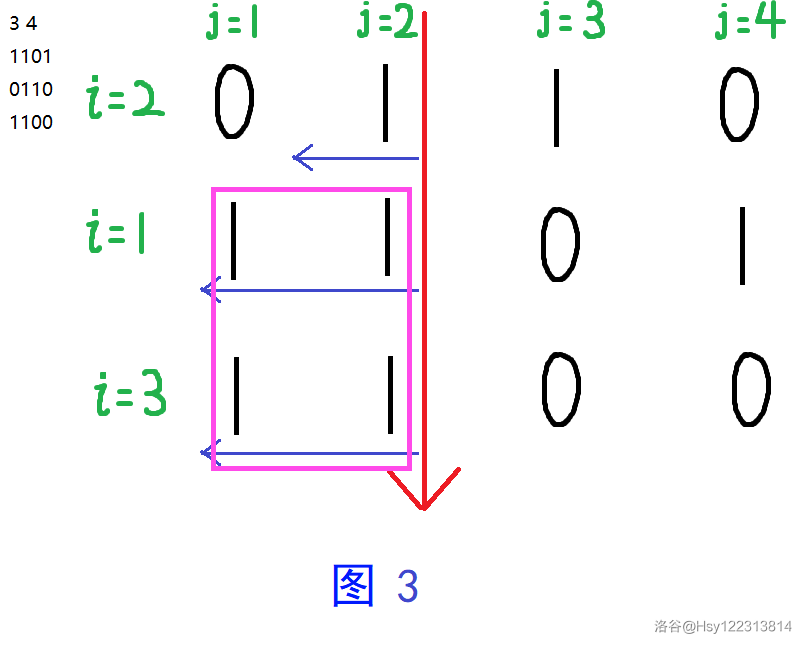
图 3 中考虑第 \(2\) 行时，最大矩形面积为 \(4\)。

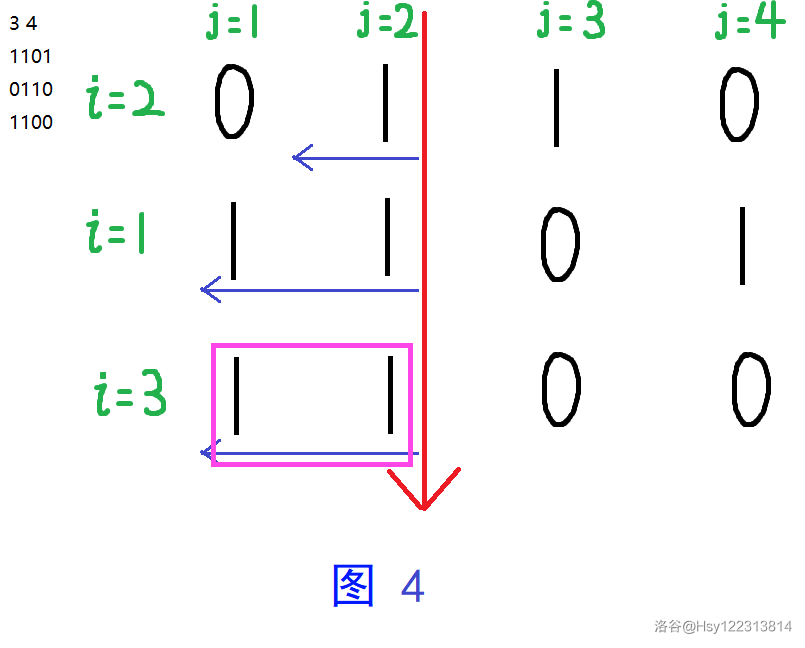
图 4 中考虑第 \(3\) 行时，最大矩形面积为 \(2\)。

\(Code\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int NR = 5010;
char a[NR][NR];
int c[NR][NR];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++)
	{
		scanf("%s", a[i] + 1);
	}
	for (int i = 1; i <= n; i ++)
	{
		for (int j = 1; j <= m; j ++)
		{
			if (a[i][j] == '1') c[j][i] = c[j - 1][i] + 1;
			else c[j][i] = 0;
		}
	}
	int ans = 0;
	for (int j = 1; j <= m; j ++)
	{
		sort(c[j] + 1, c[j] + n + 1);
		for (int i = 1; i <= n; i ++)
		{
			ans = max(ans, c[j][i] * (n - i + 1));
		}
	}
	cout << ans << endl;
	return 0;
}