洛谷题解：AT_abc245_e [ABC245E] Wrapping Chocolate

本题算法为贪心，这里主要来证明贪心的正确性。

因为对于每个盒子和巧克力都有两个属性，长和宽，不便于判断，于是考虑对 \(B\) 和 \(D\) 进行排序；又由于 当遇到每一个巧克力就想要在前面的盒子中找最合适的 ，于是必须保证前面盒子的 \(D\) 值比当前巧克力的 \(B\) 值要大，所以从大到小对 \(B\) 和 \(D\) 排序；还观察到盒子和巧克力的属性十分相似，于是将它们两个放在一个数组里排序，若 \(B\) 与 \(D\) 一致，那么盒子排在前。

但是这个贪心策略还不完善，尤其是那句斜体的话：当遇到每一个巧克力就想要在前面的盒子中找最合适的。最合适的是什么？其实应该是在前面的盒子中找最小的一个 \(\ge A\) 的 \(C\) 值。

那么为什么就对了？咱们来证明一下。

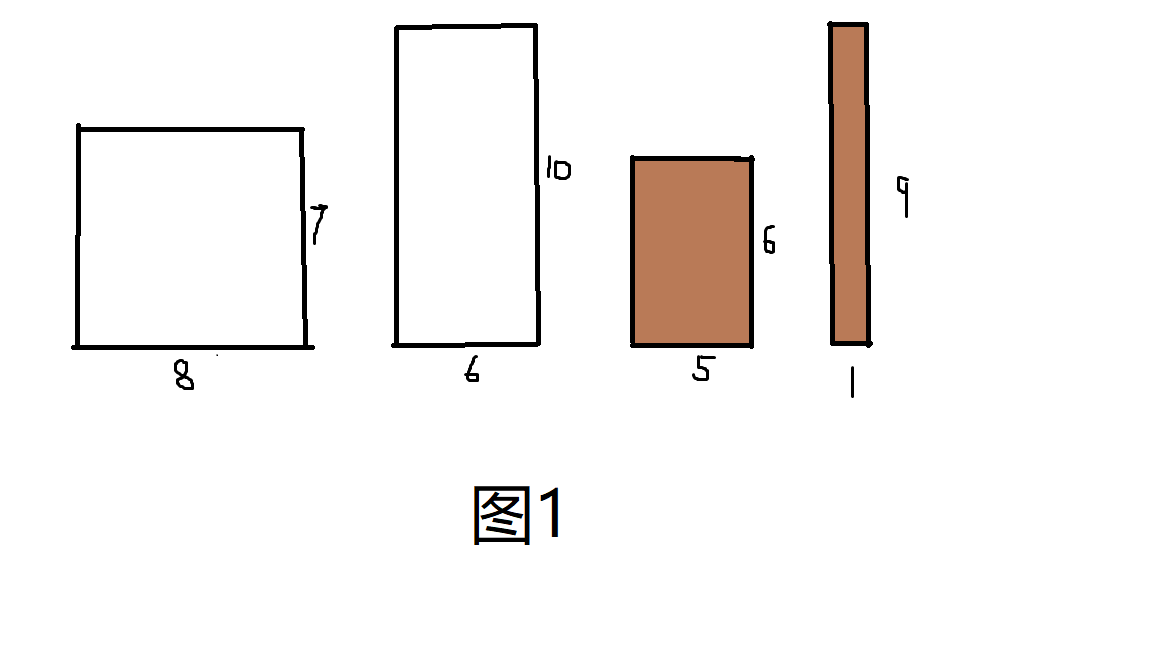
图片中白色为盒子，棕色为巧克力。

先看图1，对 \(B\) 和 \(D\) 排好序后，我们考虑第一块巧克力的匹配，一眼看去，第二个盒子的6，10最适合，但如果将第一块巧克力放到第二个盒子后，第二块巧克力该如何放置呢？还不如把第一块巧克力放在 \(C\) 值更优的第一个盒子里，这样第二块巧克力也可以放下了。

对于每块需要放置的巧克力，我们首先知道前面的 \(D\) 值都能满足这块巧克力的 \(B\) 值。其次，我们不知道，这块巧克力之后有没有比它的 \(A\) 值更大的，所以我们需要选前面盒子中 \(C\) 值尽可能小的盒子，以为后面留准备。

所以可证这种贪心策略一定最优，满足可行性原则。

\(Code\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <set>
using namespace std;

const int NR = 2e5 + 10;
multiset<int> s;

struct node
{
	int a, b, t;
	bool operator < (const node &y) const
	{
		if (b != y.b) return b > y.b;
		return t > y.t;
	}
}p[NR * 2];

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++)
	{
		scanf("%d", &p[i].a);
		p[i].t = 1;
	}
	for (int i = 1; i <= n; i ++)
	{
		scanf("%d", &p[i].b);
	}
	for (int i = 1; i <= m; i ++)
	{
		scanf("%d", &p[i + n].a);
		p[i + n].t = 2;
	}
	for (int i = 1; i <= m; i ++)
	{
		scanf("%d", &p[i + n].b);
	}
	sort(p + 1, p + n + m + 1);
	for (int i = 1; i <= n + m; i ++)
	{
		if (p[i].t == 2) s.insert(p[i].a);
		else
		{
			if (s.lower_bound(p[i].a) == s.end())
			{
				puts("No");
				return 0;
			}
			s.erase(s.lower_bound(p[i].a));
		}
	}
	puts("Yes");
	return 0;
}