NKOJ 1046 【并查集】[NOIP2010-3]关押罪犯

NKOJ 1046 【并查集】[NOIP2010-3]关押罪犯

总思路

• 对罪犯之间地关系按怨气值进行排序，排完后尽量把怨气值大的罪犯拆散。核心在于如何维护罪犯之间的敌人和在同一所监狱的关系。

方法一

思路：普通并查集

实现方法

• 对于每一个罪犯，如果他遇到了第一个敌人用数组记录他的敌人，如果他已经有敌人了就把他的两个敌人排在一起，如果不可避免地让两个有敌对关系地罪犯排在了一起，就输出。
• 安排罪犯的这个过程用普通并查集实现。

代码

#include<cstdio>
#include<algorithm>
#define int long long
using namespace std;
int n,m;
int f[100005],eny[100005];
int getf(int x){
	if(f[x]==x) return x;
	return f[x]=getf(f[x]);
}
struct node{int x,y,val;}arr[100005];
void merge(int x,int y){
	int fx=getf(x),fy=getf(y);
	if(fx!=fy) f[fx]=fy;
}
bool cmp(node a,node b){
	return a.val>b.val;
}
signed main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++) f[i]=i;
	for(int i=1;i<=m;i++) scanf("%lld%lld%lld",&arr[i].x,&arr[i].y,&arr[i].val);
	sort(arr+1,arr+1+m,cmp);
	for(int i=1;i<=m;i++){
		if(getf(arr[i].x)==getf(arr[i].y)){
			printf("%lld",arr[i].val);
			return 0;
		}
		else{
			if(eny[arr[i].x]==0) eny[arr[i].x]=arr[i].y;
			else merge(arr[i].y,eny[arr[i].x]);
			if(eny[arr[i].y]==0) eny[arr[i].y]=arr[i].x;
			else merge(arr[i].x,eny[arr[i].y]);
		}
	}
	puts("0");

	return 0;
}

方法二

思路：种类并查集(未实现)

实现方法

• 将数组开到原来的两倍大小，前 \(1 \sim n\) 表示朋友关系，后 \(n+1 \sim 2n\) 表示前 \(n\) 个人的分身，分身是专门用来连接敌人关系的。

如下图，展示的是有 \(4\) 个人，\(1\) 和 \(2\) 号是朋友，\(1\) 和 \(3\) 、\(3\) 和 \(4\) 是敌人

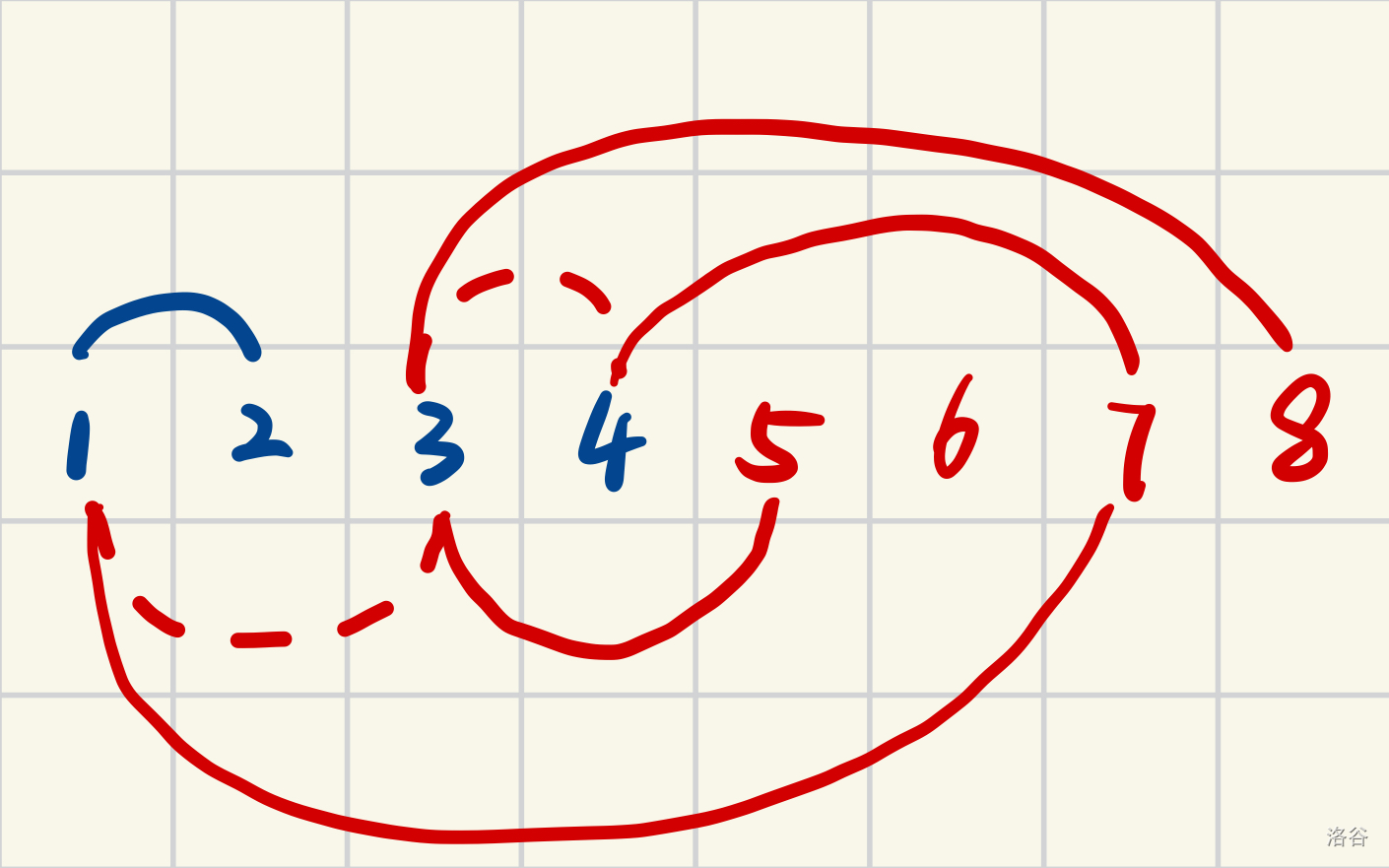
从图中可以看出，种类并查集的好处在于可以很清楚地表达敌人的敌人是朋友的关系。

• 在本题中，原本没有敌人的敌人是朋友的关系，但是我们希望将矛盾大的罪犯拆开，如果 A 有一个敌人 B，A 跟 B 的矛盾大，此时又有一个 B 的敌人 C 跟 B 的矛盾也很大，那么 A 在一号监狱，B在二号监狱，不可避免地将 C 也放在一号监狱，这和敌人的敌人是朋友这句话是异曲同工的。

总结

实际上，上述上述两种方法是一样的，只是表达敌人这种关系的方法不同。