Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color ci, connecting vertex ai and bi.
Mr. Kitayuta wants you to process the following q queries.
In the i-th query, he gives you two integers — ui and vi.
Find the number of the colors that satisfy the following condition: the edges of that color connect vertex ui and vertex vi directly or indirectly.
The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.
The next m lines contain space-separated three integers — ai, bi (1 ≤ ai < bi ≤ n) and ci (1 ≤ ci ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (ai, bi, ci) ≠ (aj, bj, cj).
The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.
Then follows q lines, containing space-separated two integers — ui and vi (1 ≤ ui, vi ≤ n). It is guaranteed that ui ≠ vi.
For each query, print the answer in a separate line.
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4
2
1
0
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4
1
1
1
1
2
Let's consider the first sample.
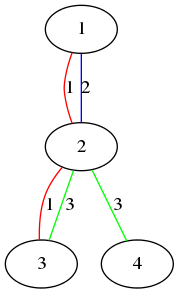 The figure above shows the first sample.
The figure above shows the first sample.- Vertex 1 and vertex 2 are connected by color 1 and 2.
- Vertex 3 and vertex 4 are connected by color 3.
- Vertex 1 and vertex 4 are not connected by any single color.
题意:n个点的图 m条边 两个点间可以有多条边 但是两点间相同颜色的边只能有一条 q个查询 判断 u-v间可以通过多少种颜色的边联通
题解:并查集处理
1 #pragma comment(linker, "/STACK:102400000,102400000") 2 #include <cstdio> 3 #include <iostream> 4 #include <cstdlib> 5 #include <cstring> 6 #include <algorithm> 7 #include <cmath> 8 #include <cctype> 9 #include <map> 10 #include <set> 11 #include <queue> 12 #include <bitset> 13 #include <string> 14 #include <complex> 15 #define ll __int64 16 #define mod 1000000007 17 using namespace std; 18 int n,m; 19 int fa[105][105]; 20 int find(int root,int c) 21 { 22 if(fa[c][root]==root) 23 return root; 24 else 25 return fa[c][root]=find(fa[c][root],c); 26 } 27 void unio(int a,int b,int c) 28 { 29 int aa=find(a,c); 30 int bb=find(b,c); 31 if(aa!=bb) 32 fa[c][aa]=bb; 33 } 34 int main() 35 { 36 scanf("%d %d",&n,&m); 37 for(int i=1;i<=m;i++) 38 for(int j=1;j<=n;j++) 39 fa[i][j]=j; 40 int a,b,c; 41 for(int i=1;i<=m;i++) 42 { 43 scanf("%d %d %d",&a,&b,&c); 44 unio(a,b,c); 45 } 46 int q; 47 scanf("%d",&q); 48 for(int i=1;i<=q;i++) 49 { 50 scanf("%d %d",&a,&b); 51 int ans=0; 52 for(int j=1;j<=m;j++) 53 { 54 if(find(a,j)==find(b,j)) 55 ans++; 56 } 57 printf("%d\n",ans); 58 } 59 return 0 ; 60 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号