HDOJ 3516 Tree Construction

四边形优化DP

Tree Construction

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 868    Accepted Submission(s): 470

Problem Description

Consider a two-dimensional space with a set of points (xi, yi) that satisfy xi < xj and yi > yj for all i < j. We want to have them all connected by a directed tree whose edges go toward either right (x positive) or upward (y positive). The figure below shows an example tree.


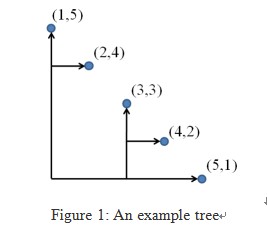
Write a program that finds a tree connecting all given points with the shortest total length of edges.

 

Input

The input begins with a line that contains an integer n (1 <= n <= 1000), the number of points. Then n lines follow. The i-th line contains two integers xi and yi (0 <= xi, yi <= 10000), which give the coordinates of the i-th point.

 

Output

Print the total length of edges in a line.

 

Sample Input

5
1 5
2 4
3 3
4 2
5 1
1
10000 0

 

Sample Output

12
0

 

Source

2010 ACM-ICPC Multi-University Training Contest（8）——Host by ECNU

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int maxn=1100;
const int INF=0x3f3f3f3f;

struct POINT
{
	int x,y;
}pt[maxn];

int n;
int dp[maxn][maxn],s[maxn][maxn];

inline int cost(int i,int j,int k)
{
	return pt[k].y-pt[j].y+pt[k+1].x-pt[i].x;
}

int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		for(int i=1;i<=n;i++)
		{
			scanf("%d%d",&pt[i].x,&pt[i].y);
		}
		for(int i=1;i<=n;i++)		
		{
			s[i][i]=i;
		}
		for(int len=2;len<=n;len++)
		{
			for(int i=1;i+len-1<=n;i++)
			{
				int j=i+len-1;
				dp[i][j]=INF;
				for(int k=s[i][j-1];k<=s[i+1][j]&&k<j;k++)
				{
					if(dp[i][j]>dp[i][k]+dp[k+1][j]+cost(i,j,k))
					{
						s[i][j]=k;
						dp[i][j]=dp[i][k]+dp[k+1][j]+cost(i,j,k);
					}
				}
			}
		}
		printf("%d\n",dp[1][n]);
	}
	return 0;
}