SVD 学习笔记
本文主要学习了这篇博客:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html,将SVD讲的恨透,特征值讲的也非常好。
特征值
矩阵分解时可以将矩阵用一组两两正交的基表示,也就是一组特征向量,而特征值就是表示每个特征向量的重要程度的数值。
奇异值
特征值是对方阵来说的,对于非方阵我们该怎么办呢,我们仿照特征分解,就有了下面的式子
假设A是一个M*N的矩阵,那么得到的U是一个M * M的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个M *N的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V’(V的转置)是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量),从图片来反映几个相乘的矩阵的大小可得下面的图片(PS:下图中用颜色方块的形状大概表示矩阵的形状)
而关于奇异值的具体求解,wikipedia 上讲的还是很好的。
注:一下为特异值的求解
对于任意的奇异值分解 ,矩阵Σ的对角线上的元素等于M的奇异值. U和V的列分别是奇异值中的左、右奇异向量。
,矩阵Σ的对角线上的元素等于M的奇异值. U和V的列分别是奇异值中的左、右奇异向量。
奇异值分解在意义上看很一般,因此它可以适用于任意m×n矩阵,而特征分解只能适用于特定类型的方阵。不过,这两个分解之间是有关联的。 给定一个M的奇异值分解,根据上面的论述,两者的关系式如下:
关系式的右边描述了关系式左边的特征值分解。于是:
奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:
r是一个远小于m、n的数,这样矩阵的乘法看起来像是下面的样子:
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Σ、V就好了。
好,到这里SVD就相当于讲完了,其核心思想就一点用前10%甚至1%的奇异值表示了全部的奇异值,因为在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了,这样做可以大大的减少数据的存储和计算。


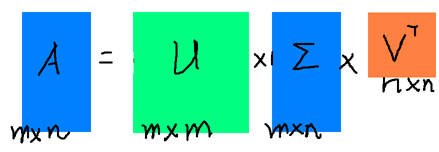


 的
的 的特征向量。
的特征向量。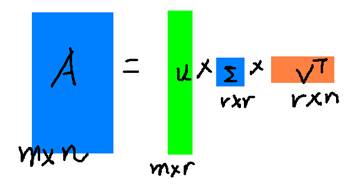

 浙公网安备 33010602011771号
浙公网安备 33010602011771号