1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

（1）回顾机器学习分类：监督学习，半监督学习，无监督学习，强化学习

 监督学习分为：回归，分类

 回归分为：线性回归，Logistic回归

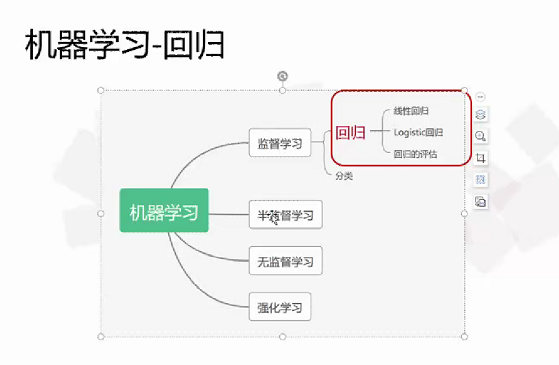
（2）回归与分类的区别：他们区别在于输出变量的类型（预测目标是否连续）

  回归：定量输出即连续变量预测（例子：预测明天的气温多少度）

  分类：定性 输出即离散变量预测（例子：预测明天是阴天还是晴天）

（3）线性回归算法应用：房价的预测，销售额的预测，银行贷款额度的预测

  房价预测代码实现：预测房价与面积的线性关系

 

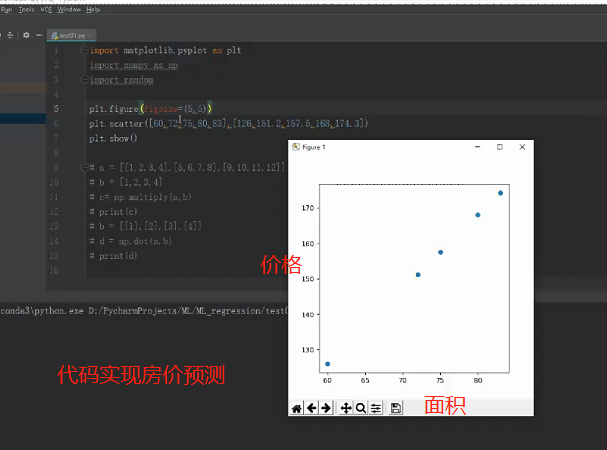
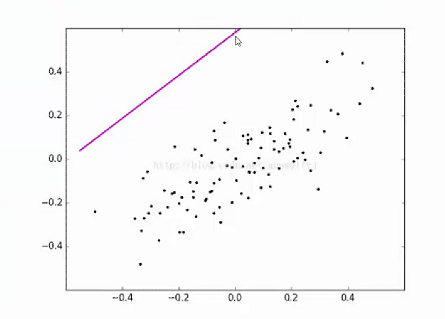
线性回归算法要实现的就是根据离散的样本数据训练出一条误差最小的线性回归方法

 

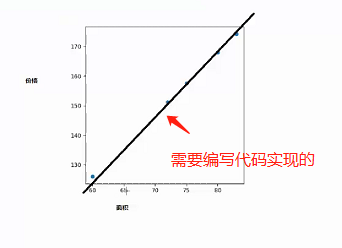
（3）线性回归算法定义：通过一个或多个自变量与因变量进行建模的回归方法。

（4）数组与矩阵的回顾

数组可以是多维的，例如：1维，2维，3维等

矩阵必须是2维的

 数组与矩阵的加法，乘法运算：

 

代码实现数组与矩阵的加法，乘法运算：

 

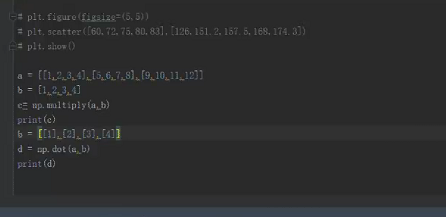
数组和矩阵的运算结果：

 

 

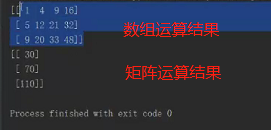
 由上面的运算结果可以看出矩阵的计算可以满足线性回归的需求，因此线性回归中选择使用矩阵

（5）在线性回归方法中，选择使用y=w*x+b（w为权重，b为截距），而不使用y=w*x，加上截距b会更加准确。如下图中，房价预测的图，起始点含有一个截距b.

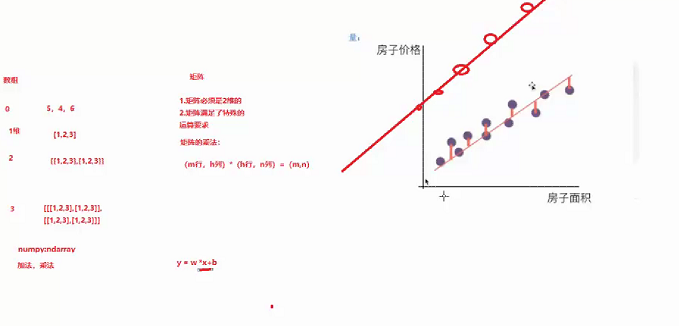
 （6）线性回归算法中预测值和真实值存在一定的误差

　单变量：

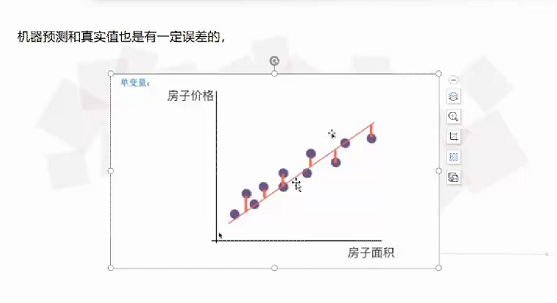
　多变量的误差：

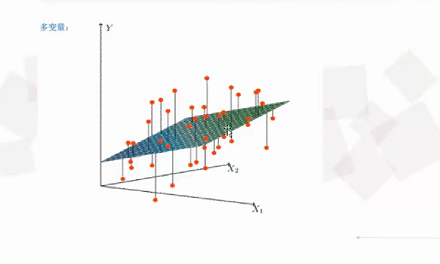
 （7）预测值和真实值存在误差，那么需要去减小误差，这时就引入了损失函数（误差的大小）

  减小误差的方法有两种：

  1.正归方程

  2.梯度下降法（重点）

 

 （8）梯度下降法的理解：沿着这个函数找，最后能找到山谷的最低点，并更新w（即权重），可以使用在训练数据规模十分庞大的情景，当特征过于复杂，求解速度会较慢。

 

梯度下降动态演示图:

 

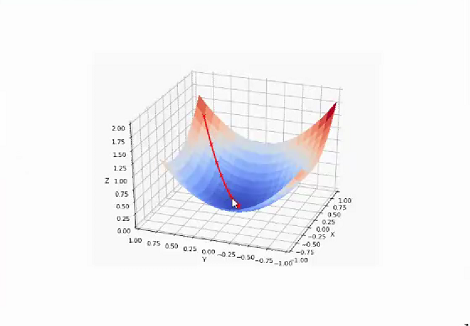
（9）梯度下降法之代码实现

 

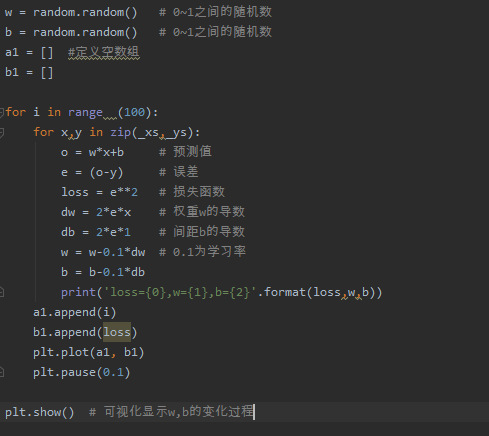
 不同训练次数运行结果：训练次数越多，误差就越小，就越接近真实值

 

从上面的loss值，w值，b值可以看出误差越来越小，越来越接近真实值。

训练10次：

 

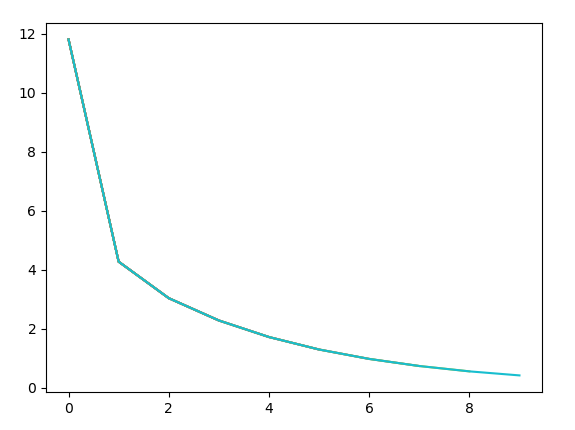
 训练50次：

 

 

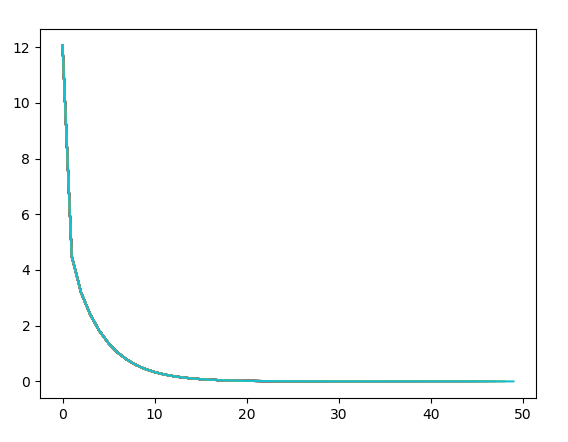
训练100次：

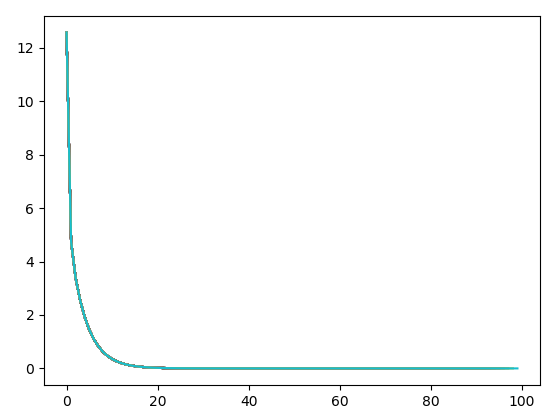
 从w,b值的可视化过程可以看出，随着训练次数增加越来越接近真实值。

 

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

（1）可以依据客户的推荐指数进行预测点击量，例如：对于书籍，我们可以根据用户对它的推荐指数，排名，价格等因素进行预测书籍的点击量。

（2）可以预测学生成绩的相对排名；根据学生的校园行为数据，例如：学生平时表现，图书馆借阅记录以及之前综合成绩的排名，将这些数据作为训练数据，预测学生本学期的期末成绩排名。

（3）依据用户的喜好对用户的消费进行预测，依据历史票房数据、影评数据、舆情数据等互联网公众数据，对电影票房进行预测。

 

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

 根据平台的书籍推荐指数，预测书籍的点击量

数据：

 

 运行截图：

 

 

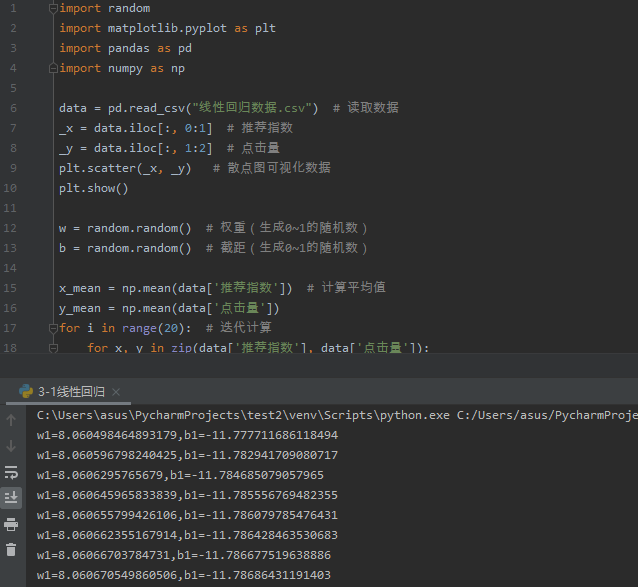
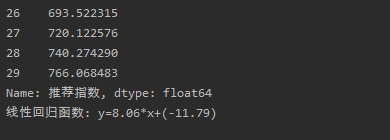
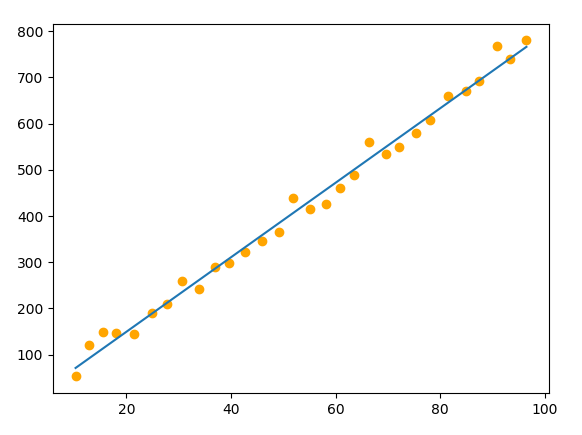
源代码：

 1 import random
 2 import matplotlib.pyplot as plt
 3 import pandas as pd
 4 import numpy as np
 5 
 6 data = pd.read_csv("线性回归数据.csv")  # 读取数据
 7 _x = data.iloc[:, 0:1]  # 推荐指数
 8 _y = data.iloc[:, 1:2]  # 点击量
 9 plt.scatter(_x, _y)   # 散点图可视化数据
10 plt.show()
11 
12 w = random.random()  # 权重（生成0~1的随机数）
13 b = random.random()  # 截距（生成0~1的随机数）
14 
15 x_mean = np.mean(data['推荐指数'])  # 计算平均值
16 y_mean = np.mean(data['点击量'])
17 for i in range(20):  # 迭代计算
18     for x, y in zip(data['推荐指数'], data['点击量']):
19         w += (x - x_mean) * (y - y_mean)
20         b += (x - x_mean) ** 2
21     w1 = w / b
22     b1 = y_mean - w1 * x_mean
23     print('w1={0},b1={1}'.format(w1, b1))  # 输出w1和b1的变化过程
24 
25 y_pre = w1*data['推荐指数']+b1
26 print("预测结果:", y_pre)
27 print("线性回归函数:", "y=%.2f*x+(%.2f)" % (w1, b1))
28 plt.scatter(_x,_y,color="orange")
29 plt.plot(_x,y_pre)
30 plt.show()