3.作业要求：

1）贴上视频学习笔记，要求真实，不要抄袭，可以手写拍照。

 P2 概率论与贝叶斯先验：

    

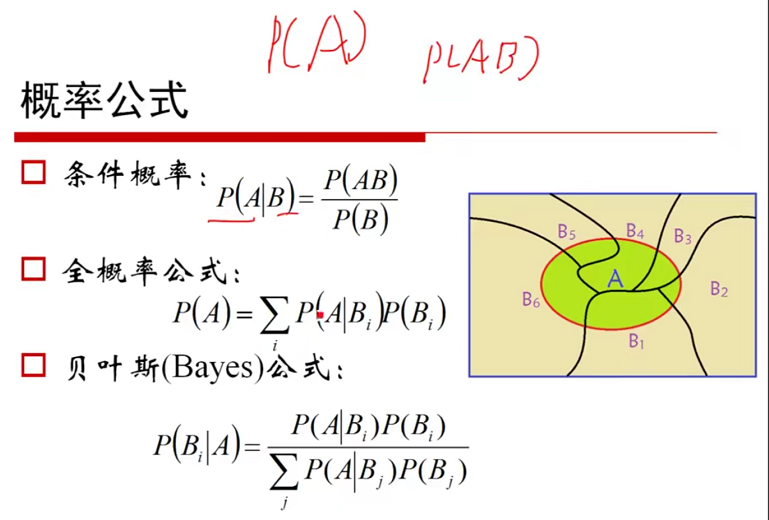
                                 图1-1概率公式（--23:00）

          

                                   图1-2 贝叶斯公式                                                                              图1-3 贝叶斯的应用

常见的分布类型：

                 

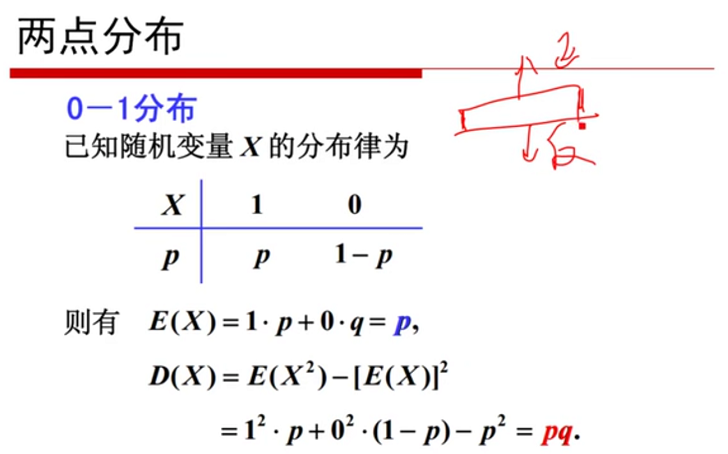
　　　　　　　　　  图1-4 两点分布　　　　　　　　　　　　　　　　　　　　　　 　图1-5 二项分布

　　　　　　　　  　图1-6 考察Taylor展式

    　　   

　　　　　 图1-7 泊松分布（--45:00）                                                                           图1-8 泊松分布事例（--46:50）

              

　　　　　　　　图1-9 均匀分布（--47:30）　　   　　　　　　　　　　　　　　　　图1-10 指数分布（--48:30）

   　　　

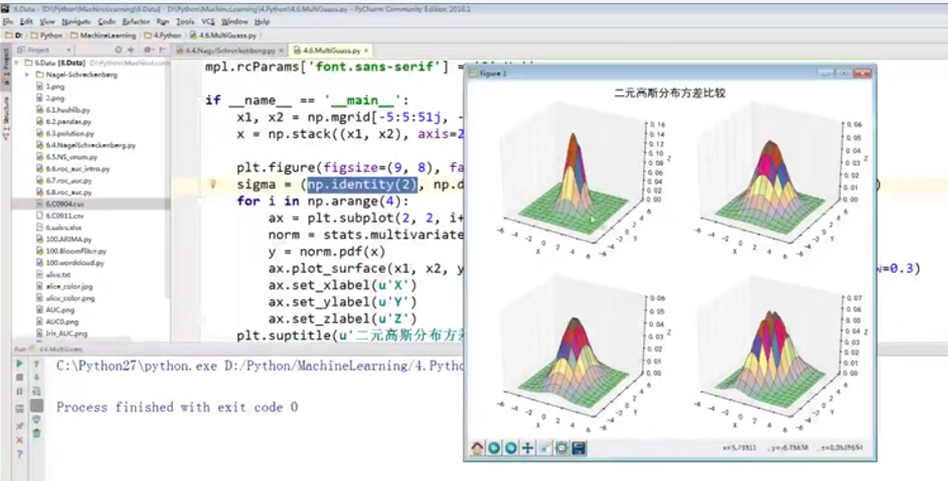
　　　　　　　  图1-11 正态分布（--53:00）　　　　　　　　　　　　　　　　　　　　 图1-12 二元高斯分布实例（--56:00）

 　　　  

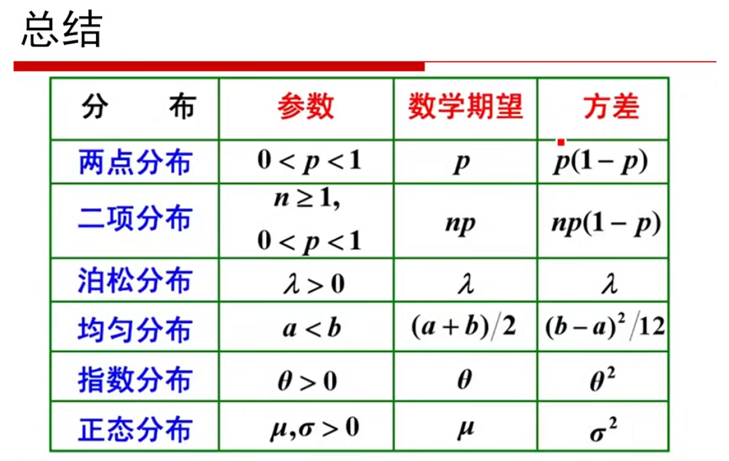
　　　　　　　  图1-13 总结（--61:00）　　　　　　　　　　　　　　　　　　　

　　     　 

　　　　　　　  图1-14 Beta分布（--61:50）　　　　　　　　　　　　　　　　　　　 图1-15 Beta分布期望（--66:00）

       　　  

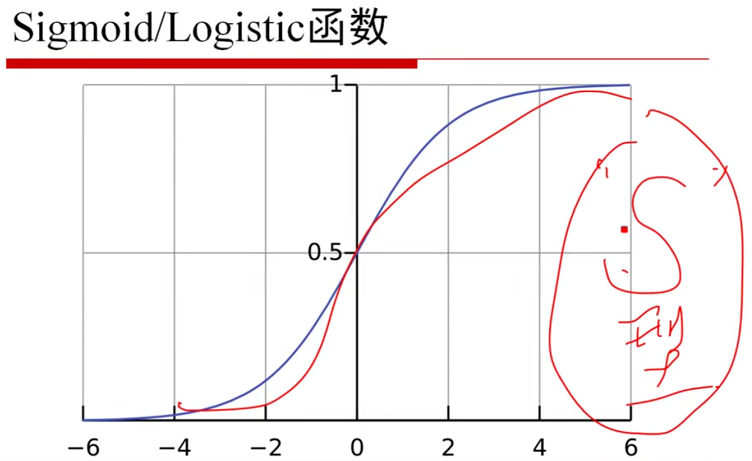
　　　　 图1-16 Sigmoid/Logistic函数（--90:30）　　　　　　　　　　　　　　　　　 图1-17 考察参数（--91:50）

 　　　　 

　　　　 图1-18 Sigmoid函数导数（--92:36）　　　　　　　　　　　　　　　　　   图1-17 考察参数（--93:50）

 

　　　　  图1-18 独立性概念（--95:30）

期望、方差以及协方差

　　　　　　

　　　　   图1-19 期望（--97:00）　　　　　　　　　　　　　　　　　   　　　　　  图1-20 期望的性质（--97:40）

　　　 　　

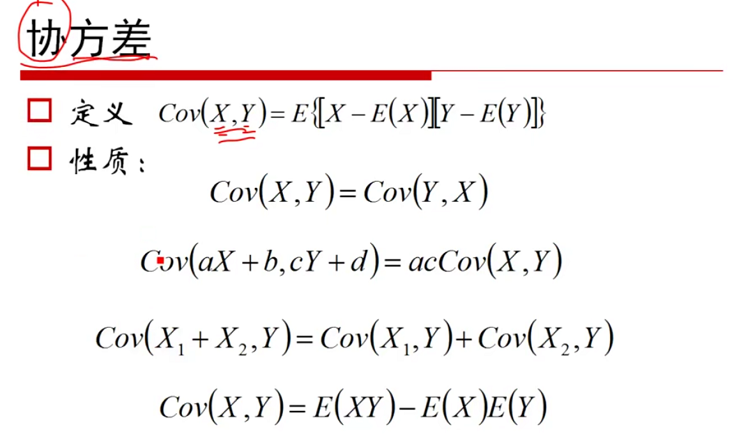
 　　　　   图1-21 方差（--103:20）　　　　　　　　　　　　　　　　　   　　　　   图1-22 协方差（--106:20）

　　　　    

 　　　　图1-23 协方差之独立、不相关（--110:00）　　　　　　　　　　　　　       图1-24 协方差的意义（--110:10）

　　　　　　

 　　　　  图1-25 协方差上界（--110:45）　　　　　　　　　　　　　　　　　　　    图1-26 上界证明（--112:10）

    　　　　

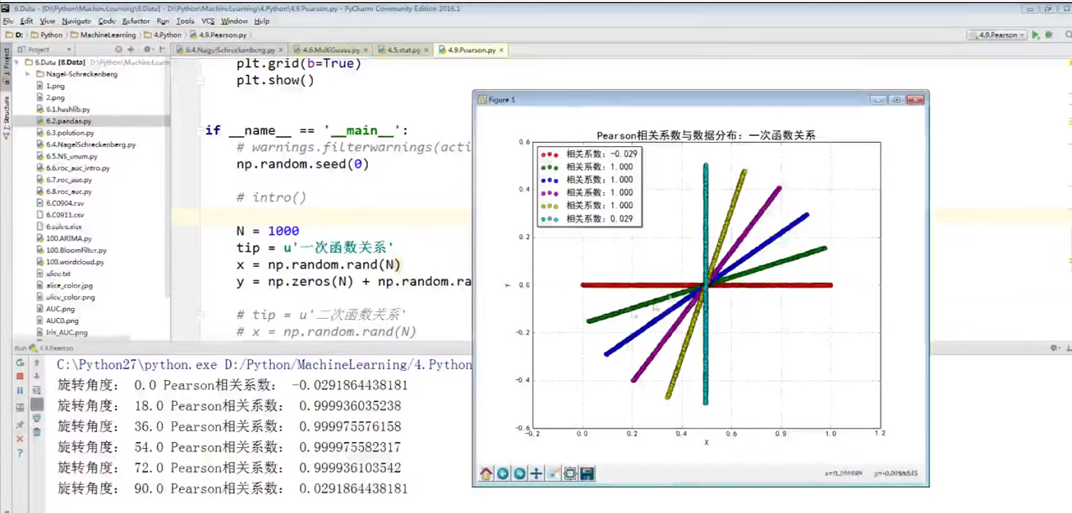
 　　　　  图1-27 Pearson相关系数（--117:00）　　　　　　　　　　　　　　　　　　　 图1-28 代码示例（--119:10）

　　　　  

 　　　　  图1-29 协方差矩阵（--126:50）　　　　　　　　　　　　　　　　　　　  图1-30 切比雪夫不等式（--137:30）

　　　 　  

 　　　　      图1-31 大数定律（--128:05）　　　　　　　　　　　　　　　　　　　   图1-32 大数定律的意义（--139:20）

    

　　　　　　　  图1-33 伯努利定理（--143:00）

 　　　　　

  　　　　       图1-34 中心极限定理（--143:50）　　　　　　　　　　　　　　　　图1-32 中心极限定理的意义（--146:40）

 

 P3 矩阵和线性代数：

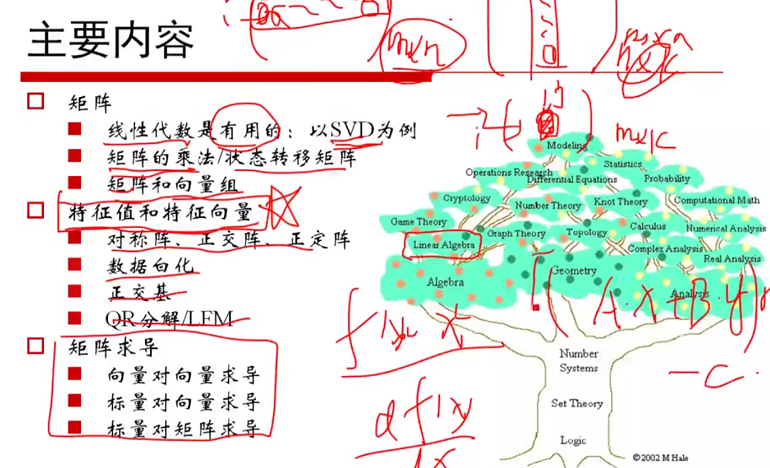
　　　　　　　　图2-1 本章内容（--00:50）

　　　　　

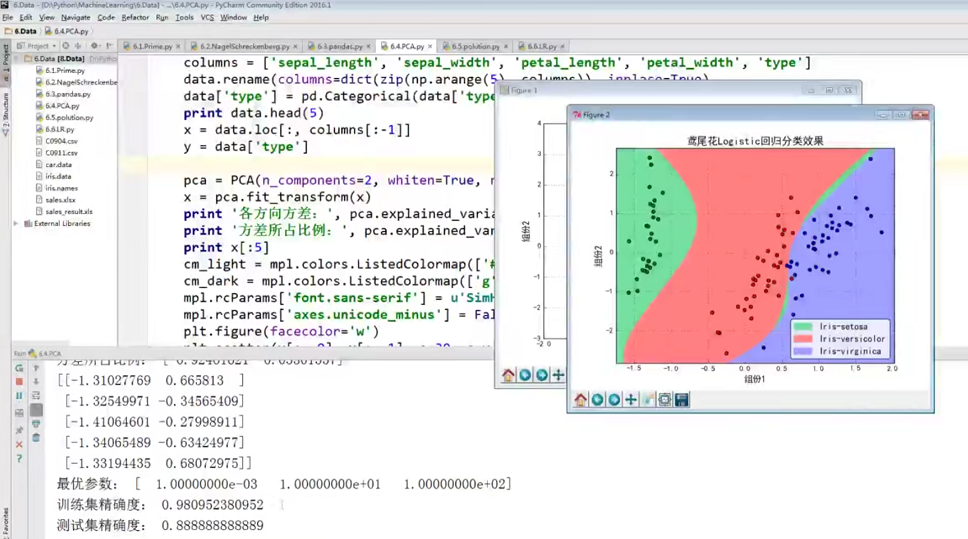
　　　　　　　　图2-2 SVD提法（--04:00）　　　　　　　　　　　　　　　　　　　　　　　　　图2-2 降维实例（--15:00）

　　　　　

　　　　　　　　图2-3 线性代数（--16:00）　　　　　　　　　　　　　　　　　　　图2-4 行列式（--17:00）

　　　　  

 　　　　　　　  图2-5 代数余子式（--18:00）　　　　　　　　　　　　　　　　　　　图2-6 伴随矩阵（--19:20）　

　　　　　　 

　　　　　　     图2-7 方阵的逆（--20:00）　　　　　　　　　　　　　　　　　　　　图2-8 范德蒙行列式（--20:20）

　　　　　  　 

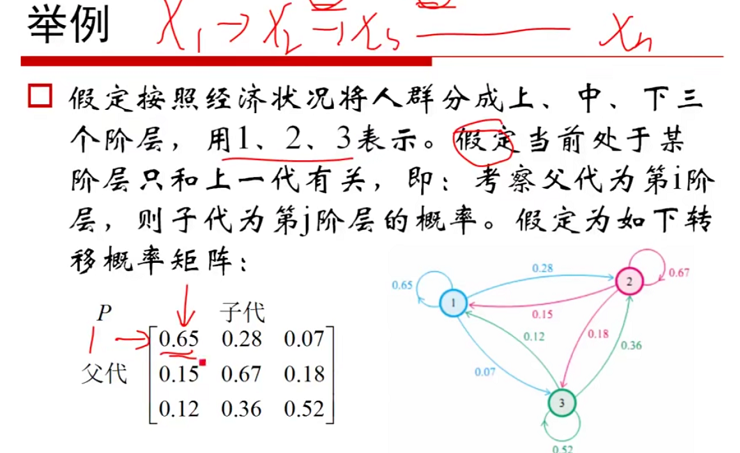
     　　　　　　图2-9 矩阵的乘法（--25:10）　　　　　　　　　　　　　　　　　　　图2-8 乘法举例（--28:10）

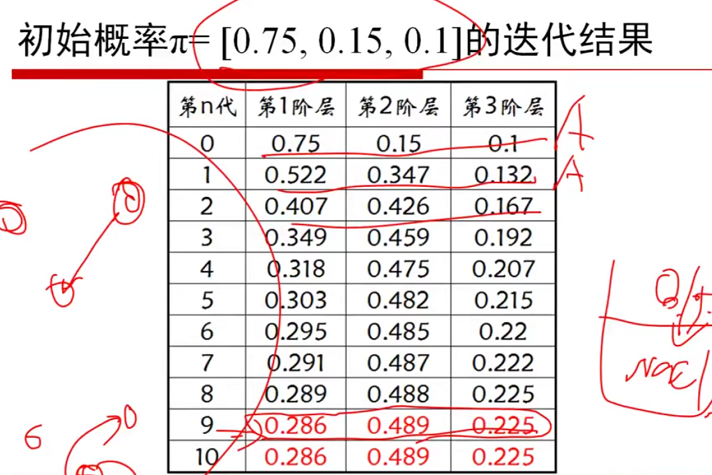
     　　　　  图2-11 π的迭代结果（--34:00）

                     

     　　　　　图2-12 平稳分布概念（--37:20）     　　　　　　　　　　　　　　　　　图2-13 平稳分布（--38:00）

　　　　 　

　　　　　　图2-14 矩阵和向量的乘法（--42:00）　　　　　　　　　　　　　　　　图2-15 矩阵的秩（--46:00）

　　 　　

 

 　　　　图2-15 秩与线性方程（--49:20）

　　　    　   

 　　　　图2-16 向量组等价定义（--52:00）　　　　　　　　　　　　　　　　图2-17 系数矩阵（--53:00）

　　　　　　

 　　　　  图2-18 正交阵概念（--56:20）　　　　　　　　　　　　　　　　　　图2-19 特征值和特征向量（--62:00）

　　　　   图2-20 实对称阵正交结论（--66:00）

 　　　　 图2-21 白化/漂白（--73:00）

　　　　　

 　　　　 图2-22 正定阵概念（--78:00）　　　　　　　　　　　　　　　　　　　　图2-23 正定阵的判定（--80:30）

　　　　  　

 　　　　  图2-24 QR分解（--84:20）　　　　　　　　　　　　　　　　　　　　　 图2-25 计算特征值（--87:30）

 　　　　      　　图2-26 LFM（--91:10）

 

     　　　　　　图2-27 偏导结论（--96:00）

　　　　　  

     　　　图2-28 标量对向量的导数（--98:40）　　　　　　　　　　　　　　　　图2-29 标量对方阵的导数（--102:00）

 

2）用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”，可以word编辑，可做思维导图，可以手写拍照，要求言简意赅、排版整洁。

(1) 梯度：

在机器学习中，我们通常需要对问题进行建模，然后可以得到一个成本函数。在函数中每个点都有相应的方向导数，梯度即为函数在某一个点的一个向量，而它的方向与取得最大的方向导数的方向一致，模为该方向导数的最大值。

导数：

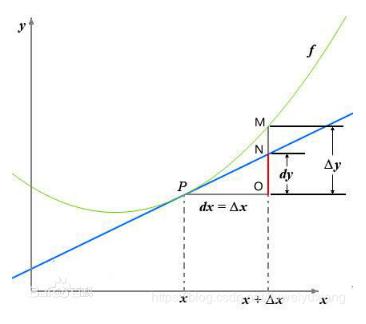
梯度的求解：

 

梯度模型：

 

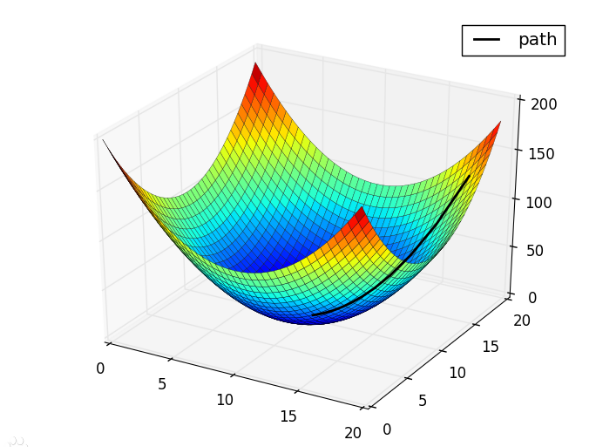
 (2) 梯度下降：

通俗来讲，梯度下降就是从群山中的山顶找到一条最短的路走到山谷最低的地方。

而梯度下降法是一种优化算法，该算法从任一点开始，沿该点梯度的反方向运动一段距离，再沿新位置的梯度反方向运行一段距离，反复迭代。解一直朝下坡最陡的方向运动，希望能运动到函数的全局最小点。（梯度下降不一定是全局最优解，有可能是局部最优解）

梯度下降图解：

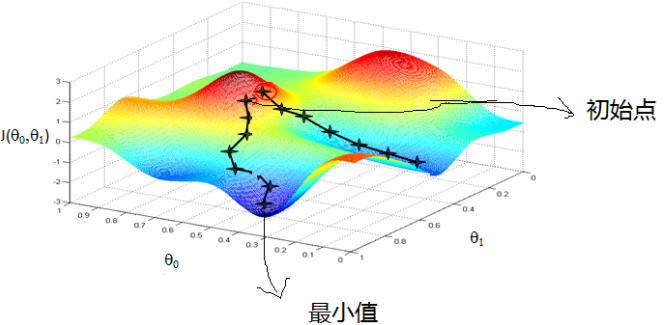
(3) 贝叶斯定理：

通俗来讲，在运用概率对某一事件进行推断之前，我们往往已经事先掌握了关于这一事件的概率，这个概率可能是主观概率或者相对概率，这种初始的概率可以称为先验概率。如果在后续的研究中，通过抽样调查样本等消息源又获得了有关该事件的信息，我们就可以根据这些新信息对先验概率进行修正，使先验概率变为后验概率。这个修正概率的定理就称为贝叶斯定理。

 贝叶斯公式：

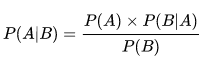
P(A)是A的先验概率或边缘概率。称为"先验"是因为它不考虑任何B方面的因素。
P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
P(B)是B的先验概率或边缘概率。称为"先验"是因为它不考虑任何A方面的因素。
P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。