迪杰斯特拉（Dijkstra）算法实现

一、效果图

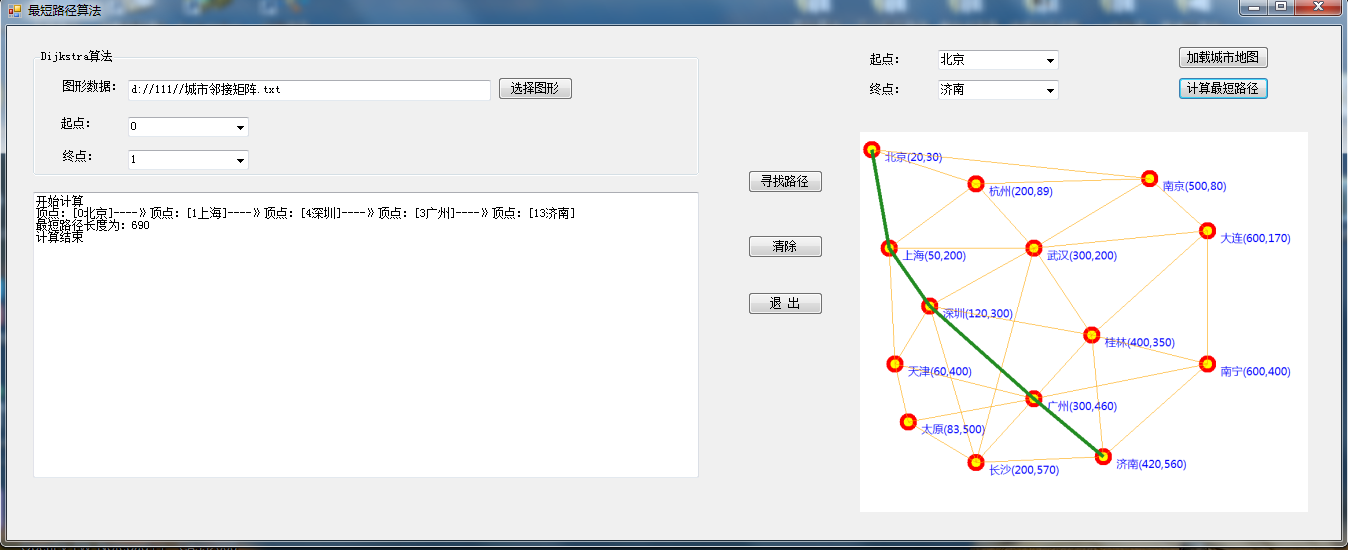
 二、构造图

 2.1 城市坐标

创建文件：城市列表.txt

北京 20 30
上海 50 200
天津 60 400
广州 300 460
深圳 120 300
杭州 200 89
南京 500 80
长沙 200 570
南宁 600 400
桂林 400 350
武汉 300 200
太原 83 500
大连 600 170
济南 420 560

 2.2 城市网络

创建文件：城市邻接矩阵.txt

14
0 172 99999 99999 99999 189 482 99999 99999 99999 99999 99999 99999 99999
172 0 200 99999 122 186 99999 99999 99999 99999 250 99999 99999 99999
99999 200 0 247 116 99999 99999 99999 99999 99999 99999 102 99999 99999
99999 99999 247 0 240 99999 99999 148 305 148 99999 220 99999 156
99999 122 116 240 0 99999 99999 281 99999 284 205 99999 99999 99999
189 186 99999 99999 99999 0 300 99999 99999 99999 149 99999 99999 99999
482 99999 99999 99999 99999 300 0 99999 99999 99999 233 99999 134 99999
99999 99999 99999 148 99999 99999 99999 0 99999 99999 99999 136 99999 220
99999 99999 99999 305 99999 99999 99999 99999 0 206 99999 99999 230 240
99999 99999 99999 148 284 99999 99999 99999 206 0 180 99999 269 210
99999 250 99999 99999 205 149 233 383 99999 180 0 99999 301 99999
99999 99999 102 220 99999 99999 99999 136 99999 99999 99999 0 99999 99999
99999 99999 99999 99999 99999 99999 134 99999 230 269 301 99999 0 99999
99999 99999 99999 156 99999 99999 99999 220 240 210 99999 99999 99999 0

二、算法实现

C#代码如下：

 /**
         *  函数名： runDjsktra_path(迪杰斯特拉算法)
         *  输入参数：
         *  int pStart      ：起始端点
         *  int pEnd        ：结束端点
         *  int[,] pGraph   ：图
         *  函数描述：输入起始端点、图，
         *  返回：算出起始端点到结束端点的最短路径所经过的所有顶点列表
         *  作者：黄庆飞
         *  日期：2020-12-28
         **/
        public ArrayList runDjsktra_path(int pStart, int pEnd, int[,] pGraph) //运行迪杰斯特拉算法
        {
             ArrayList al_path = new ArrayList(); //最短路径顶点轨迹列表            
            try
            {  
                int i_count = pGraph.Length;//获取整个二维数组的长度，即所有元的个数
                int i_rank = pGraph.Rank; //数组的秩
                int i_row = pGraph.GetLength(0); //二维数组行数
                int i_column = pGraph.GetLength(1);//二维数组列数
                int i_vetex_count = i_row; //顶点数量
                int[] dist = new int[i_vetex_count];  //各个顶点到起始点的最短路径中间状态
                int[] visit = new int[i_vetex_count]; //顶点是否访问过标志
                int[] PathArc=new int[i_vetex_count]; // 存储最短路径下标

                //由起始点信息更新状态
                for (int i = 0; i < i_vetex_count; i++)
                {
                    dist[i] = pGraph[pStart, i];
                    visit[i] = 0;
                    PathArc[i] = pStart;

                }
                visit[pStart] = 1;//起始点已访问过，标志设置为1                

                //开启循环
                for (int i = 0; i < i_vetex_count; i++)
                {
                    int min_dist = 99999;//存储从起始节点到其他未被访问节点中的最短距离
                    int middle = 0; //存储最短距离节点的编号
                    for (int j = 0; j < i_vetex_count; j++)
                    {
                        if (visit[j] == 0 && min_dist > dist[j])
                        {
                            min_dist = dist[j];
                            middle = j;  
                        }
                    }
                    visit[middle] = 1; //将middle顶点设置为已访问                     
                    for (int k = 0; k < i_vetex_count; k++)
                    {
                        int temp = min_dist + pGraph[middle, k];
                        if (visit[k] == 0 && dist[k] > temp)
                        {
                                dist[k] = temp;
                                PathArc[k] = middle;  
                        }
                    }
                }
                //回溯路径
                int i_prior = PathArc[pEnd];
                al_path.Add(pEnd);
                while (i_prior!=pStart)
                {
                    al_path.Add(i_prior);
                    i_prior = PathArc[i_prior];
                }
                al_path.Add(pStart);
                al_path.Reverse();//回溯后进行反转，由起点出发
                return al_path;   //返回start到end的最短路径经过的顶点列表
            }
            catch (Exception ex)
            {
                return null;
            }
        }