20182316胡泊 第10周学习总结
20182316胡泊 2019-2020-1 《数据结构与面向对象程序设计》第10周学习总结
教材学习内容总结
第十九章 图
什么是图
1.图的概念
-
概念：我理解的图就是由内容和相互关系组成的非线性的存储数据的形式，具体来说就是由结点来存储元素，连线代表关系。
-
树中的每个结点都只有一个父结点，如果我们允许一个结点连通多个其他结点，树就变成了图。
-
术语：
- 顶点(Vertex)：图中的数据元素。
- 边(Edge)：图中各个顶点之间的连接。
- 邻接/邻居：两个顶点之间有一条边，则称这两个顶点是邻接的。
- 路径：连接两个顶点之间的一系列边称为两个顶点间的路径，边的条数称为路径长度（路径长度=顶点数-1）。
- 环路：首顶点与末顶点相同且路径中没有边重复的路径。
-
分类：
- 【是否有方向】无向图和有向图
- 【每条边带有权重或代价】加权图/网络（加权图可以是有向的也可以是无向的）
1.无向图
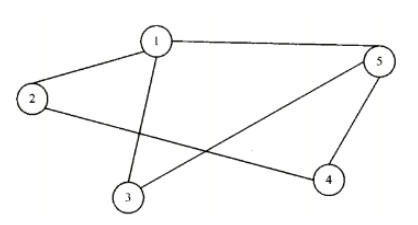
- 无向图:是一种边为无序结点对的图。在无向图中，(A,B)(B,A)指的是一条边，表示A与B之间有一条两个方向都连通的边。
- 完全：一个无向图是完全的，说明对于有n个顶点的无向图，图中有n(n-1)/2条边。
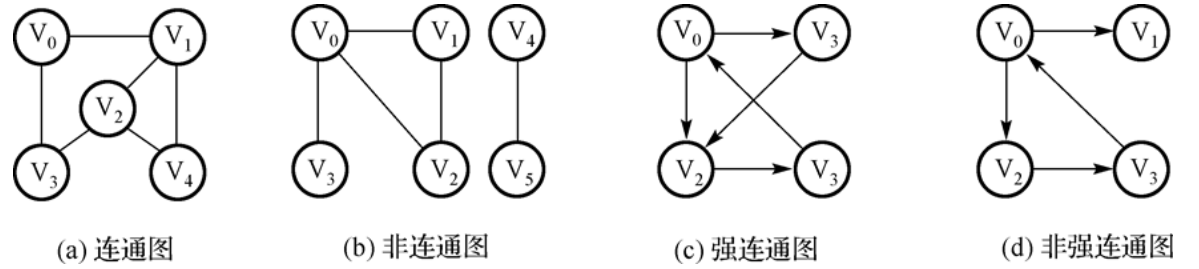
- 连通：如果无向图中的任何两个顶点之间都存在一条路径，则认为该无向图是连通的。
- 同时连通还分为强连通和弱连通（非强连通），强连通图中，任何两个顶点之间都是连通的，就是说任何两个顶点之间都至少有一条路径。
- 完全图一定是连通图，连通图不一定是完全图。
- 无向树：一种连通的没有环路的，其中一个元素被指定为树根的图。
2.有向图
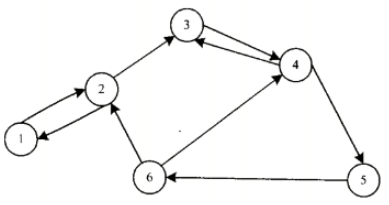
- 有向图/双向图是一种边为有序顶点对的图。在无向图中，<A,B><B,A>指的不是一条边，<A,B>表示从A到B有一条连通的边，但B到A没有。
3.加权树
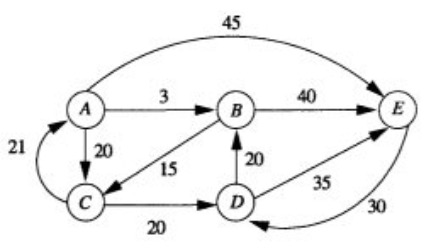
- 加权图：是一种每条边都带有权重或代价的图。加权图中，某一条路径的权重等于该路径中所有边权重的总和。
- 加权图中边的表示：在普通的图中，我们表示边时只需要起始顶点和终止顶点即可，但是在加权图中，除了上面的两项外还需要增加一个表示权重的元素。例如在有向图中，从A到B之间有一条边，权重为3，那么它的表示就为(A,B,3)
4.生成树
- 概念：一颗含有图中所有顶点和部分边的树。一个图的生成树不一定是唯一的。
- 最小/大生成树：树中的路径权重总和小于/大于它所来源的图中的任何一颗生成树的权重总和。
图的算法
1.遍历
- 图的遍历分为两种：广度优先遍历（简称BFS，与树中的层序遍历类似）深度优先遍历（简称DFS，与树中的前序遍历类似）。
- 广度优先遍历——使用一个队列和一个无序列表来实现，队列用于管理遍历，无序列表用于存储遍历结果。
- 第一步：起始顶点进入队列，标记为已访问。
- 第二步：从队列中取出起始顶点加入无序列表的末端，让与该顶点相连的还未被标记为已访问的顶点加入队列中，把它们都标记为已访问。
- 第三步：重复第二步的操作，每次取出队列中的首个顶点加入无序列表，直至队列为空。
- 深度优先遍历——使用一个栈和一个无序列表来实现，栈的作用与广度优先遍历中队列的作用相同。
- 第一步：起始顶点进入栈。
- 第二步：从栈中取出起始顶点加入无序列表的末端，标记为已访问，让与该顶点相连的顶点加入栈中。
- 第三步：重复第二步的操作，每次取出栈顶元素加入无序列表，把顶点标记为已访问，直至栈为空。
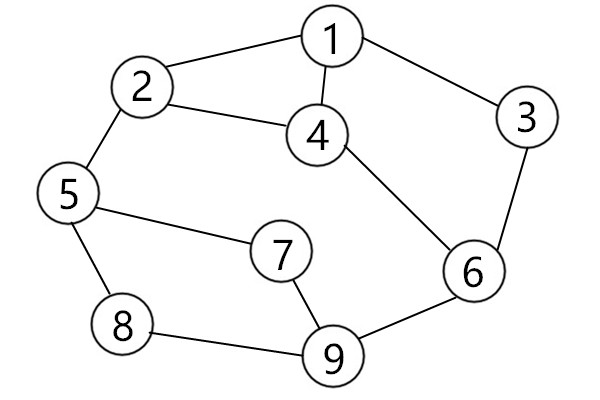
- 例子
-
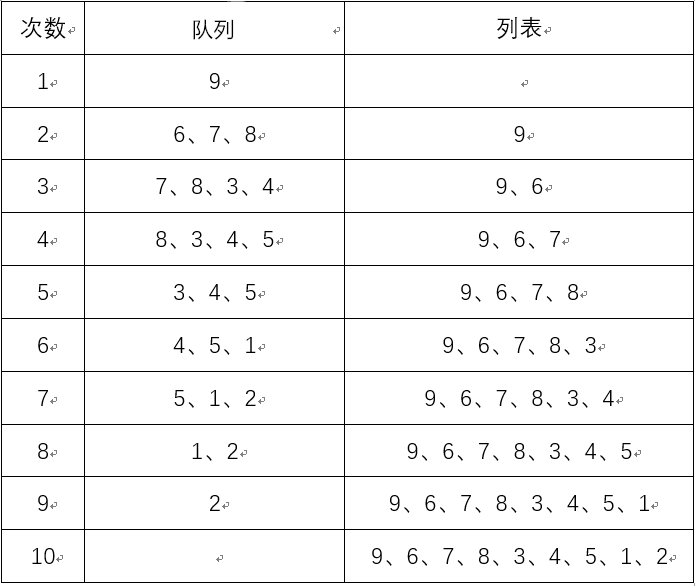
广度优先遍历：9、6、7、8、3、4、5、1、2
-
过程：
-
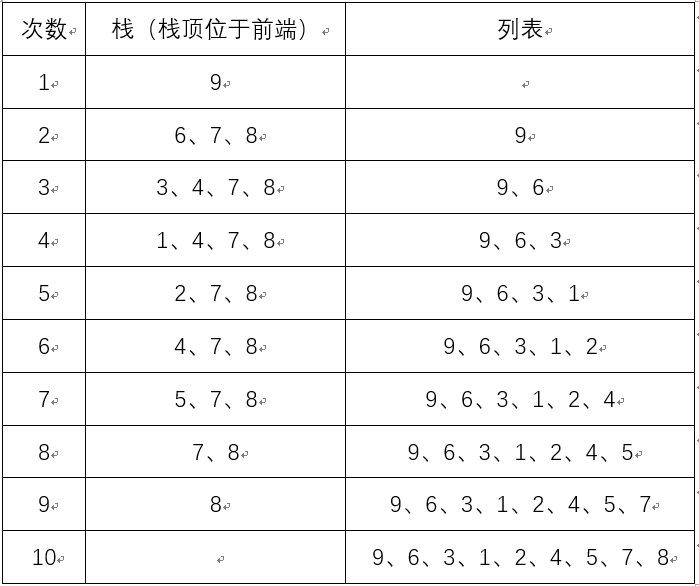
深度优先遍历：9、6、3、1、2、4、5、7、8
-
过程：
-
2.测试连通性
- 要判断一个图的连通性，需要确定图中的任意两个顶点之间都有一条路径，如果直接判断的话时间复杂度会很大。书上给出了一种简单的判断方法：在一个含n个顶点的图中，当且仅当图中的每个顶点的广度优先遍历的无序列表长度都为n时，证明该图就是连通的。
3.最小生成树
- 推衍算法（以最小生成树为例）：在寻找最小树的过程中需要一个最小堆用于每次寻找最小边
- 1.从图中任选一个起始顶点，将它添加到最下生成树中
- 2.将所有含起始顶点的边按照权重由小到大的顺序加入到最小堆中
- 3。从最小堆中选出权重最小的边，将该边和与该边连接的最小生成树中没有的顶点加入最小生成树中，加入的顶点成为新的起始顶点。
- 4.重复第二和第三步直至最小生成树中含有图的所有顶点或最小堆为空时。
图的实现
1.邻接列表
- 邻接列表是一种特殊的链表，它有点像解决哈希排序地址冲突时用的中的链地址法。对于无向图而言，一条边会同时出现在边两边的两个顶点的邻接列表中。对于加权图而言，每条边还会存储一个值代表该边的权重。
2.邻接矩阵
- 邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，该图的邻接矩阵有n行n列，每一个点代表了两个顶点之间的一条边。对于无向图，如果A1和A2之间有一条边，那么在二维矩阵中，[A1,A2]和[A2,A1]处的值为1。对于有向图，如果A1和A2之间有且仅有一条A1指向A2的边，那么[A1,A2]处的值为1，[A2,A1]处的值为0。对于加权图，把相应位置的1换成权值即可。
教材学习及代码调试中的问题和解决过程
- 问题1：如何实现深度优先遍历？
- 问题1解决方案：通过我上网查询以及自己的思考、修改后，使用一个栈和一个无序列表来实现，栈用于管理遍历，无序列表用于存储遍历结果，步骤如下：
- 第一步：起始顶点进入栈。
- 第二步：从栈中取出起始顶点加入无序列表的末端，标记为已访问，让与该顶点相连的顶点加入栈中。
- 第三步：重复第二步的操作，每次取出栈顶元素加入无序列表，把顶点标记为已访问，直至栈为空。
- 代码如下：
public Iterator iteratorBFS(int startIndex){
Integer x;
QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
UnorderedListADT resultList = new ArrayUnorderedList();
// 若所给索引值无效，抛出错误
if (!indexIsValid(startIndex)){
throw new ElementNotFoundException("Graph");
}
// 设置每个顶点是否被访问，初始设置为未访问
boolean[] visited = new boolean[numVertices];
for (int i = 0;i < numVertices;i++){
visited[i] = false;
}
// 起始顶点进入队列，并标记为已访问
traversalQueue.enqueue(startIndex);
visited[startIndex] = true;
// 开始循环，每次把队列中的首顶点添加到resultList中，将与首顶点连接的还未进入队列的顶点加入队列，并标记为已访问
while (!traversalQueue.isEmpty()){
x = traversalQueue.dequeue();
resultList.addToRear(vertices.get(x).getElement());
for (int i = 0;i < numVertices;i++){
if (hasEdge(x,i) && !visited[i]){
traversalQueue.enqueue(i);
visited[i] = true;
a++;
}
}
}
return new GraphIterator(resultList.iterator());
}
// 判断两顶点之间是否有边
public boolean hasEdge(int a,int b){
if (a == b){
return false;
}
VerticeNode vertex1 = vertices.get(a);
VerticeNode vertex2 = vertices.get(b);
while (vertex1 != null){
if (vertex1.getElement() == vertex2.getElement()){
return true;
}
vertex1 = vertex1.getNext();
}
return false;
}
代码托管
上周考试错题总结
无
结对及互评
-
博客中值得学习的或问题：
- 对上周的错题进行了仔细的更正和课后复习，我对上周考试题的复习较为草率。
- 博客撰写详细，有理有据。
- 在撰写博客的过程中可以加入更多自己的理解。
-
代码中值得学习的或问题：
- 代码风格良好，便于阅读。
-
基于评分标准，我给本博客打分：14分。得分情况如下：
-
正确使用Markdown语法（加1分）：
- 不使用Markdown不加分
- 有语法错误的不加分（链接打不开，表格不对，列表不正确...）
- 排版混乱的不加分
-
模板中的要素齐全（加1分）
- 缺少“教材学习中的问题和解决过程”的不加分
- 缺少“代码调试中的问题和解决过程”的不加分
- 代码托管不能打开的不加分
- 缺少“结对及互评”的不能打开的不加分
- 缺少“上周考试错题总结”的不能加分
- 缺少“进度条”的不能加分
- 缺少“参考资料”的不能加分
-
教材学习中的问题和解决过程（2分）
-
代码调试中的问题和解决过程（3分）
-
本周有效代码超过300分行的（加1分）
-
其他加分：
- 周五前发博客的加1分
- 感想，体会不假大空的加1分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 错题学习深入的加1分
- 点评认真，能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
点评过的同学博客和代码
- 本周结对学习情况
-
结对照片
-
结对学习内容
对上周及本周的考试内容进行了探讨，并通过上网查询等方式深入分析，直到将问题理解。
一起制作博客，markdown，遇到问题相互询问，并解决。
其他（感悟、思考等，可选）
- 这周主要是在忙安卓的事情，我负责的代码部分任务量不少，因此在java上用的时间就减少了许多，老师也十分体谅我们，将实践课时间给我们用来写Android，接下来会更加努力走完最后一段路程。
学习进度条
| 代码行数（实际/预期） | 博客量（新增/累积） | 学习时间（新增/累积） | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | |||
| 第一周 | 119/119 | 3/3 | 20/20 | |
| 第二周 | 302/300 | 2/5 | 25/45 | |
| 第三周 | 780/800 | 2/7 | 25/70 | |
| 第四周 | 1500/1300 | 2/9 | 25/95 | |
| 第五周 | 3068/2500 | 3/12 | 25/120 | |
| 第六周 | 4261/4000 | 2/14 | 25/145 | |
| 第七、八周 | 7133/7000 | 3/17 | 25/170 | |
| 第九周 | 10330/10000 | 3/20 | 25/195 | |
| 第十周 | 11600/11000 | 2/22 | 15/210 |
-
计划学习时间:25小时
-
实际学习时间:15小时
