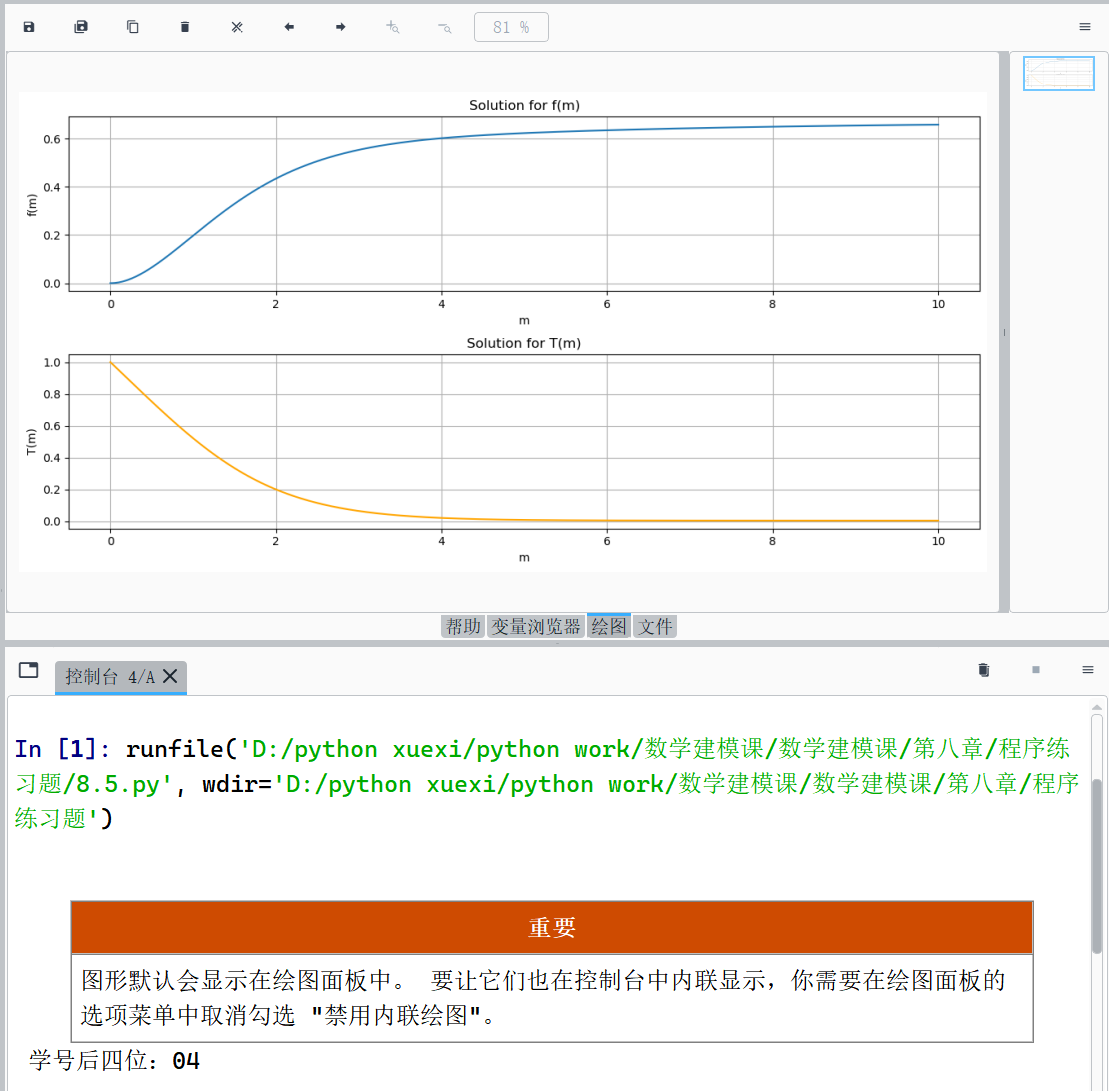
8.5 求微分方程组(竖直加热板的自然对流)的数值解。(d^3f)/(dm^3)+3f(d^f)/(dm^2)-2((df)/(dm))^2+T=0,(d^2T)/(dm^2)+2.1f(dT)/(dm)=0，已知当m=0时,f=0,(df)/(dm)=0,(d^2f)/(dm^2)=0.68,T=1,(dT)/(dm)=-0.5。要求在[0,10]区间上，画出f(a)、T(a)的解曲线

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

def model(t, y):
f, df_dm, d2f_dm2, T, dT_dm = y
d3f_dm3 = -3fd2f_dm2 + 2(df_dm)**2 - T
d2T_dm2 = -2.1f*dT_dm
return [df_dm, d2f_dm2, d3f_dm3, dT_dm, d2T_dm2]

y0 = [0, 0, 0.68, 1, -0.5]

t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

sol = solve_ivp(model, t_span, y0, t_eval=t_eval, method='RK45')

f = sol.y[0]
T = sol.y[3]

plt.figure(figsize=(12, 6))

plt.subplot(2, 1, 1)
plt.plot(sol.t, f, label='f(m)')
plt.xlabel('m')
plt.ylabel('f(m)')
plt.title('Solution for f(m)')
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(sol.t, T, label='T(m)', color='orange')
plt.xlabel('m')
plt.ylabel('T(m)')
plt.title('Solution for T(m)')
plt.grid(True)

plt.tight_layout()
plt.show()

print("学号后四位：04")