1.4 长度的相对性与费兹杰惹—洛伦兹收缩

写在前面的一些废话

精神方面的赞助商们要求的标题真是越来越长了呢
1.3.1中我们详细讲解了洛伦兹因子和爱因斯坦延缓，可以说洛伦兹因子贯穿了整个相对论，而爱因斯坦延缓是接下来的几章的基石，所以我建议没有认真看的同学再去看一遍。（请注意我在1.3.1中说的不是跳过1.3.1这一章，而是跳过练习部分）

长度的相对性

首先我们思考一下：测量一个高速运动的物体，你应该怎么做。
答案可能有两种
第一种：追上去量，当你和待测物体的相对速度为0时，就能非常容易的测量出该物体长度。
第二种：当运动物体经过静止尺时，读出读数。
但是仔细一想不难发现：如果运动物体长度的确会缩短的话，第一种方法中追上去量，用于测量的尺也会缩短，无法达到实验目的。
所以说最合理的方法是，记录下物体两端“同时”的位置，然后再测量他们的距离
不急着推导，我们先复习一下1.2 “同时”不同时中讲过的一个情景。

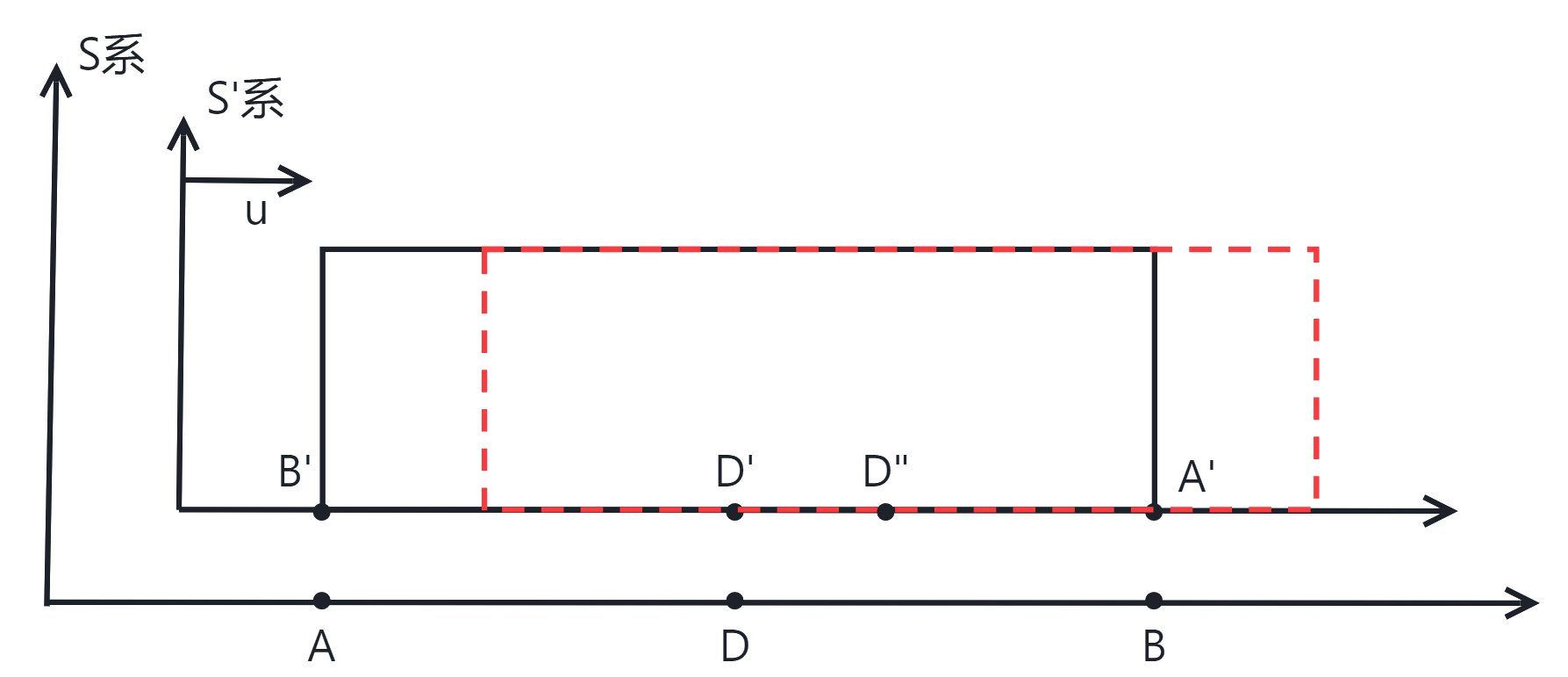
在那个情景中，我们探讨了在不同参考系中，对于同一运动物体的测量长度不同

费兹杰惹—洛伦兹收缩

注意这两个名字之间是半个破折号，不是数字“一”！

情景

一直尺（\(S'系\)）相对地面（\(S系\)）以速度\(u\)向右运动，尺的左端\(A'\)发出闪光，经尺的右端\(B'\)反射，回到\(A'\)

对于\(S'系\)，光脉冲往返时间\(Δt_0=\frac{2h}{c}\)
对于\(S系\)
光脉冲往：\(l+u·Δt_1=c·Δt_1⇒Δt_1=\frac{l}{c-u}\)
光脉冲返：\(l-u·Δt_2=c·Δt_2⇒Δt_2=\frac{l}{c+u}\)
所以在\(S\)系中，光脉冲往返时间为：
\(Δt=Δt_1+Δt_2=\frac{2cl}{c^2-u^2}\)
若考虑时间膨胀，\(Δt_0\)为本征时间
则有\(Δt=Δt_0·γ\)
\(⇒\frac{2cl}{c^2-u^2}=\frac{2l_0}{c}·γ\)
\(⇒\frac{c^2}{c^2-u^2}·l=l_0·γ\)
\(⇒\frac{1}{1-\frac{u^2}{c^2}}·l=l_0·\frac{1}{\sqrt{1-\frac{u^2}{c^2}}}\)
\(⇒l=l_0·\sqrt{1-\frac{u^2}{c^2}}=\frac{l_0}{γ}\)

结论

在\(S系\)中测量\(S'系\)（运动）的物体长度缩短了
\(l_0\)为相对参考系静止的尺的长度
和本征时间一样，我们定义它为本征长度，或静长
其次，由相对性原理，运动的尺测量静止的物体（当然没人会这么干），测量结果会比静止时长
学会了那我们就做几道练习加深记忆吧

练习1：飞船

某星球距离地球6光年，一飞船以相对地球\(u=0.6c\)的速度飞向该天体，求该飞船测量得该天体与地球的距离，以及地球与飞船参考系中飞船单程所需的时间。
解：
老规矩，先求\(γ\)
\(γ=\frac{1}{\sqrt{1-\frac{u^2}{c^2}}}=\frac{1}{0.8}=1.25\)
在\(S'系\)中，\(l'=\frac{l_0}{γ}=\frac{6}{1.25}=4.8光年\)
在\(S'系\)中，\(Δt_0=\frac{4.8光年}{0.6c}=8年\)
在\(S系\)中，\(Δt=\frac{6光年}{0.6c}=10年\)

宇宙列车

有一在太空中的太空列车（废话，不在太空中在哪里？）静长\(l_0=3×10^8m\)，高速掠过一个静止的观察者，该观测者记录通过时间为\(0.75秒\)，求列车的相对速度
这道题（我想出来）有三种方法，但只会详细讲两种
解：
法一：
在\(S系\)中，\(0.75秒\)为本征时间
\(Δt_0=0.75=\frac{3}{4}\)
车长：\(l=\frac{l_0}{γ}=l_0·\sqrt{1-\frac{u^2}{c^2}}\)
有\(\frac{l_0·\sqrt{1-\frac{u^2}{c^2}}}{u}=\frac{3}{4}秒\)
\(⇒u=0.8c\)
法二：
在\(S'\)系中，观察者经过车头、车尾时间间隔
\(Δt=Δt_0·γ=\frac{Δt_0}{\sqrt{1-\frac{u^2}{c^2}}}\)
\(\frac{l_0}{u}=\frac{Δt_0}{\sqrt{1-\frac{u^2}{c^2}}}\)
\(⇒u=0.8c\)
只要单纯地带公式就行了，感觉很简单是不是？
第三种方法就是使用间隔时间进行计算，在这就不加赘述了。