网络流模板以及推导
最大流
最大流模板-Dinic
#include <bits/stdc++.h>
using namespace std;
const int N = 10010,M = 2e5+10,INF = 0x3f3f3f3f;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int n,m,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver]==d[u]+1&&f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
flow += t,f[i]-=t,f[i^1]+=t;
}
}
return flow;
}
int dinic()
{
int flow,r = 0;
while(bfs())while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d%d%d",&n,&m,&S,&T);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
printf("%d\n",dinic());
return 0;
}
上下界
无源汇上下界可行流
#include <bits/stdc++.h>
using namespace std;
const int N = 210,M = (10200+N)*2,INF = 0x3f3f3f3f;
int h[N],e[M],ne[M],f[M],l[M],idx;
int d[N],q[N],cur[N],A[N];
int n,m,S,T;
void add(int a,int b,int c,int d)
{
e[idx] = b,f[idx] = d-c,l[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int hh = 0,tt = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(hh<=tt)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow= 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver]==d[u]+1&&f[i])
{
int t = find(ver,min(f[i],limit-flow));
if(!t) d[ver] = -1;
flow += t,f[i] -=t,f[i^1]+=t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow=find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
S = 0,T = n+1;
for(int i = 0;i<m;i++)
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
add(a,b,c,d);
A[a] -= c,A[b] += c;
}
int tot = 0;
for(int i = 1;i<=n;i++)
{
if(A[i]>0) add(S,i,0,A[i]),tot += A[i];
else if(A[i]<0) add(i,T,0,-A[i]);
}
if(dinic()!=tot) puts("NO");
else
{
puts("YES");
for(int i = 0;i<2*m;i+=2)
{
printf("%d\n",f[i^1]+l[i]);
}
}
return 0;
}
有源汇上下界最大流
#include <bits/stdc++.h>
using namespace std;
const int N = 440,M = (10000+N) * 2,INF = 0x3f3f3f3f;
int h[N],e[M],f[M],ne[M],idx;
int d[N],cur[N],q[N],A[N];
int n,m,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i= ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver]==d[u]+1&&f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
flow += t,f[i]-=t,f[i^1]+=t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
int s,t;
scanf("%d%d%d%d",&n,&m,&s,&t);
S = 0,T = n+1;
while(m--)
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
add(a,b,d-c);
A[b] += c,A[a] -=c;
}
int tot = 0;
for(int i = 1;i<=n;i++)
{
if(A[i]>0) add(S,i,A[i]),tot+=A[i];
else if(A[i]<0) add(i,T,-A[i]);
}
add(t,s,INF);
if(dinic()<tot) puts("No Solution");
else
{
S = s,T = t;
int res = f[idx-1];
f[idx-1] = f[idx-2] = 0;
printf("%d\n",res+dinic());
}
return 0;
}
有源汇上下界最小流
#include <bits/stdc++.h>
using namespace std;
const int N = 500010,M = (N+125003) * 2,INF = 2147483647;
int h[N],e[M],ne[M],f[M],idx;
int q[N],cur[N],d[N],A[N];
int n,m,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(hh<=tt)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
cur[ver] = h[ver];
d[ver] = d[t] + 1;
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver]==d[u]+1&&f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,flow += t,f[i^1]+=t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow=find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
int s,t;
scanf("%d%d%d%d",&n,&m,&s,&t);
S = 0,T = n+1;
while(m--)
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
add(a,b,d-c);
A[a] -=c,A[b] += c;
}
int tot = 0;
for(int i = 1;i<=n;i++)
{
if(A[i]>0) add(S,i,A[i]),tot += A[i];
else if(A[i]<0) add(i,T,-A[i]);
}
add(t,s,INF);
if(dinic()!=tot) puts("No Solution");
else
{
int res = f[idx-1];
S = t,T = s;
f[idx-1] = f[idx-2] = 0;
printf("%d\n",res-dinic());
}
return 0;
}
最大流求解二分图匹配
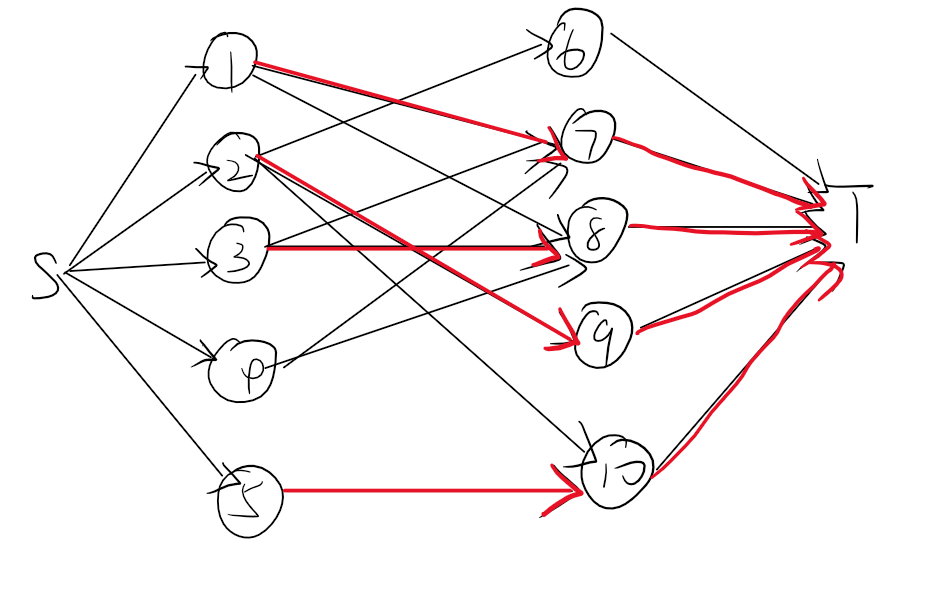
思路大致是把所有匹配点分成两部分,S(源点)向左边的匹配点(可以自己定义),连一条容量为1的边,表示这个点有一个人,左边的匹配点向右边的可匹配点连一条容量是1的边(表示左边的人可以跟右边的人完成一次匹配),右边的匹配点向汇点T连一条容量是1的边
洛谷-飞行员匹配问题
#include <bits/stdc++.h>
using namespace std;
const int N = 110,M = 10010,INF = 0x3f3f3f3f;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int n,m,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(f[i]&&d[ver]==-1)
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(f[i]&&d[ver]==d[u]+1)
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
flow += t,f[i] -= t,f[i^1]+=t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs())while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&m,&n);
S = 0,T = n+1;
for(int i = 1;i<=m;i++) add(S,i,1);
for(int i = m+1;i<=n;i++) add(i,T,1);
int a,b;
while(scanf("%d%d",&a,&b),a!=-1) add(a,b,1);
printf("%d\n",dinic());
for(int i = 0;i<idx;i+=2)
{
if(e[i]>m&&e[i]<=n&&!f[i])
{
printf("%d %d\n",e[i^1],e[i]);
}
}
return 0;
}
洛谷-圆桌问题
#include <bits/stdc++.h>
using namespace std;
const int N = 500,M = N*N,INF = 1e9;
int h[N],e[M],f[M],ne[M],idx;
int cur[N],q[N],d[N];
int n,m,S,T;
int r[N],des[N];
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
int tt = 0,hh = 0;
memset(d,-1,sizeof d);
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1&& f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
int ver = e[i];
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&m,&n);
S = 0,T = n+m+1;
int tot = 0;
for(int i = 1;i<=m;i++)
{
int x;
scanf("%d",&x);
add(S,i,x);
tot += x;
}
for(int i = 1;i<=n;i++)
{
int x;
scanf("%d",&x);
add(i+m,T,x);
}
for(int i = 1;i<=m;i++)for(int j = 1;j<=n;j++) add(i,j+m,1);
if(tot == dinic())
{
puts("1");
for(int i = 1;i<=m;i++)
{
for(int j = h[i];~j;j = ne[j])
{
if(e[j]>m&&e[j]<=m+n&&!f[j])
{
printf("%d ",e[j]-m);
}
}
puts("");
}
}
else puts("0");
return 0;
}
最大流判定问题
POJ-神秘挤奶机
二分最长边的长度mid,如果大于mid不建边,小于mid建立容量为1的边。
#include <bits/stdc++.h>
using namespace std;
const int N = 210,M = 80010,INF = 1e8;
int h[N],e[M],ne[M],w[M],f[M],idx;
int q[N],cur[N],d[N];
int n,m,T;
void add(int a,int b,int c)
{
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,w[idx] = c,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = 1,d[1] = 0,cur[1] = h[1];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == n) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==n) return limit;
int flow = 0;
for(int i = cur[u];~i && flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(1,INF)) r += flow;
return r;
}
bool check(int mid)
{
for(int i = 0;i<idx;i++)
{
if(w[i]<=mid)
{
f[i] = 1;
}
else f[i] = 0;
}
return dinic() >= T;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d%d",&n,&m,&T);
for(int i = 0;i<m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int l = 0,r = 1e6;
while(l<r)
{
int mid = l + r >> 1;
if(check(mid)) r = mid;
else l = mid + 1;
}
printf("%d",r);
return 0;
}
洛谷-星际转移问题
#include <bits/stdc++.h>
using namespace std;
const int D = 1050,N = D * 15,M = N * 4,INF = 1e9;
int h[N],e[M],ne[M],f[M],idx;
struct Ship
{
int h,r,id[30];
}ships[30];
int d[N],cur[N],q[N];
int n,m,k,S,T;
int p[N];
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
int find(int x)
{
if(p[x]!=x) p[x] = find(p[x]);
return p[x];
}
int get(int day, int i)
{
return day * (n + 2) + i;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
int ver = e[i];
cur[u] = i;
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d%d",&n,&m,&k);
S = N - 1, T = N - 2;
for(int i = 0; i < 30;i++) p[i] = i;
for(int i = 0;i<m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
ships[i] = {a,b};
for(int j = 0;j<b;j++)
{
int id;
scanf("%d",&id);
if(id == -1) id = n+1;
ships[i].id[j] = id;
if(j)
{
int b = ships[i].id[j-1];
p[find(b)] = find(id);
}
}
}
if(find(0)!=find(n+1)) puts("0");
else
{
add(S,get(0,0),k);
add(get(0,n+1),T,INF);
int day = 1,res = 0;
while(true)
{
add(get(day,n+1),T,INF);
for(int i = 0;i<=n+1;i++)
{
add(get(day-1,i),get(day,i),INF);
}
for(int i = 0;i<m;i++)
{
int r = ships[i].r,h = ships[i].h;
int a = ships[i].id[(day-1)%r],b = ships[i].id[day%r];
add(get(day-1,a),get(day,b),h);
}
res += dinic();
if(res >= k) break;
day ++;
}
printf("%d\n",day);
}
return 0;
}
拆点:用于解决点的使用限制
POJ-餐饮:三分图匹配
#include <iostream>
#include <algorithm>
#include <cstring>
#define howardlhhhr ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N = 410,M = 40610,INF = 1e9;
int h[N],e[M],ne[M],f[M],idx;
int cur[N],d[N],q[N];
int n,F,D,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
d[S] = 0,q[0] = S,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i && flow < limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
flow += t,f[i] -= t,f[i^1] += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
cin >> n >> F >> D;
S = 0,T = n*2 + F + D + 1;
for(int i = 1;i<=F;i++) add(S,n * 2 + i,1);
for(int i = 1;i<=D;i++) add(n*2+F+i,T,1);
for(int i = 1;i<=n;i++)
{
int a,b,c;
cin >> a >> b;
add(i,n+i,1);
while(a--)
{
cin >> c;
add(n*2+c,i,1);
}
while(b--)
{
cin >> c;
add(n + i,n*2+F+c,1);
}
}
cout << dinic() << endl;
return 0;
}
洛谷-最长不下降子序列问题
#include <bits/stdc++.h>
using namespace std;
const int N = 1010,M = 251010,INF = 1e9;
int h[N],e[M],ne[M],f[M],idx;
int cur[N],d[N],q[N];
int g[N],w[N];
int n,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u];~i && flow < limit; i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d",&n);
for(int i = 1;i<=n;i++) scanf("%d",&w[i]);
S = 0,T = 2 * n + 1;
int s = 0;
for(int i = 1;i<=n;i++)
{
g[i] = 1;
add(i,i+n,1);
for(int j = 1;j<i;j++)
{
if(w[j]<=w[i])
{
g[i] = max(g[j]+1 ,g[i]);
}
}
for(int j = 1;j<i;j++)
{
if(w[j]<=w[i]&&g[i] == g[j]+1)
{
add(n+j,i,1);
}
}
s = max(s,g[i]);
if(g[i] == 1) add(S,i,1);
}
for(int i = 1;i<=n;i++) if(g[i] == s) add(n+i,T,1);
printf("%d\n",s);
if(s==1) printf("%d\n%d\n",n,n);
else
{
int res = dinic();
printf("%d\n",res);
for(int i = 0;i<idx;i+=2)
{
int a = e[i^1],b = e[i];
if(a == S && b == 1) f[i] = INF;
else if(a == 1 && b == n + 1) f[i] = INF;
else if(a == n && b == n + n) f[i] = INF;
else if(a == n + n && b == T) f[i] = INF;
}
printf("%d\n",res + dinic());
}
return 0;
}
POJ-企鹅游行
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 1010,M = 5e5+10,INF = 1e9;
const double eps = 1e-8;
int h[N],e[M],ne[M],f[M],idx;
int cur[N],d[N],q[N];
int n,S,T;
double D;
PII p[N];
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx]= h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool check(PII a,PII b)
{
double dx = a.x - b.x,dy = a.y - b.y;
return dx * dx + dy * dy < D*D + eps;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
int ver = e[i];
cur[u] = i;
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
void solve()
{
memset(h,-1,sizeof h);
scanf("%d%lf",&n,&D);
S = N-1;
int tot = 0;
for(int i = 0;i<n;i++)
{
int x,y,a,b;
scanf("%d%d%d%d",&x,&y,&a,&b);
p[i] = {x,y};
add(S,i,a);
add(i,i+n,b);
tot += a;
}
for(int i = 0;i<n;i++)
{
for(int j = i+1;j<n;j++)
{
if(check(p[i],p[j]))
{
add(i+n,j,INF);
add(j+n,i,INF);
}
}
}
int cnt = 0;
for(int i = 0;i<n;i++)
{
T = i;
for(int j = 0;j<idx;j+=2)
{
f[j] += f[j^1];
f[j^1] = 0;
}
if(dinic() == tot) cnt ++,printf("%d ",i);
}
if(!cnt) puts("-1");
else puts("");
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
solve();
}
return 0;
}
最小割
最小割模板-Dinic
#include <bits/stdc++.h>
using namespace std;
const int N = 10010,M = 2e5+10,INF = 0x3f3f3f3f;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int n,m,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver]==-1&&f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver==T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u==T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver]==d[u]+1&&f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
flow += t,f[i]-=t,f[i^1]+=t;
}
}
return flow;
}
int dinic()
{
int flow,r = 0;
while(bfs())while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d%d%d",&n,&m,&S,&T);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
printf("%d\n",dinic());
return 0;
}
最大密度子图
推导及结论

POJ-生活的艰辛
把scanf printf puts改成c++模式
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 110,M = (1010+N*2)*2+10,INF = 1e8;
const double eps = 1e-8;
int h[N],e[M],ne[M],idx;
double f[M];
int q[N],cur[N],d[N];
int n,m,S,T;
PII edges[M];
bool st[N];
int dg[N],ans;
void add(int a,int b,double c,double d)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = d,ne[idx] = h[b],h[b] = idx++;
}
void dfs(int u)
{
st[u] = true;
if(u!=S) ans ++;
for(int i = h[u]; ~i ;i = ne[i])
{
int ver = e[i];
if(!st[ver] && f[i] > 0)
{
dfs(ver);
}
}
}
void build(double g)
{
memset(h,-1,sizeof h);
idx = 0;
for(int i = 0;i<m;i++) add(edges[i].x,edges[i].y,1,1);
for(int i = 1;i<=n;i++)
{
add(S,i,m,0);
add(i,T,m + 2 * g - dg[i],0);
}
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t]; ~i ;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1 && f[i] >0 )
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == T) return true;
q[++tt] = ver;
}
}
}
return false;
}
double find(int u,double limit)
{
if(u == T) return limit;
double flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver] == d[u] + 1 && f[i] > 0)
{
double t = find(ver,min(limit-flow,f[i]));
if(t<=0) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
double dinic(double g)
{
build(g);
double r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
scanf("%d%d",&n,&m);
S = 0,T = n+1;
for(int i = 0;i<m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
edges[i] = {a,b};
dg[a] ++,dg[b] ++;
}
double l = 0,r = m;
while(r-l>eps)
{
double mid = (l+r) / 2;
double t = dinic(mid);
if(m * n - t>0) l = mid;//推导的结论
else r = mid;
}
dinic(l);
dfs(S);
if(!ans) puts("1\n1");
else
{
printf("%d\n",ans);
for(int i = 1;i<=n;i++)
{
if(st[i]) printf("%d\n",i);
}
}
return 0;
}
加入点权和边权推导

洛谷-最大获利(最大密度子图解法)
#include <bits/stdc++.h>
using namespace std;
const int N = 5010,M = (N * 2 + 50000) * 2 + 10,INF = 1e8;
int h[N],e[M],ne[M],f[M],idx;
int cur[N],q[N],d[N];
int n,m,S,T;
int p[N],dg[N];
void add(int a,int b,int c,int d)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = d,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
d[S] = 0,cur[S] = h[S],q[0] = S;
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u];~i&&flow<limit;i = ne[i])
{
int ver = e[i];
cur[u] = i;
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
S = 0,T = n+1;
for(int i = 1;i<=n;i++) scanf("%d",&p[i]),p[i] *= -1;
int U = 0;
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c,c);
dg[a] += c,dg[b] += c;
}
for(int i = 1;i<=n;i++) U = max(U,2 * p[i] + dg[i]);
for(int i = 1;i<=n;i++) add(S,i,U,0),add(i,T,U - 2 * p[i] - dg[i],0);
printf("%d\n",(U*n - dinic())/2);
return 0;
}
最大权闭合子图
推导过程
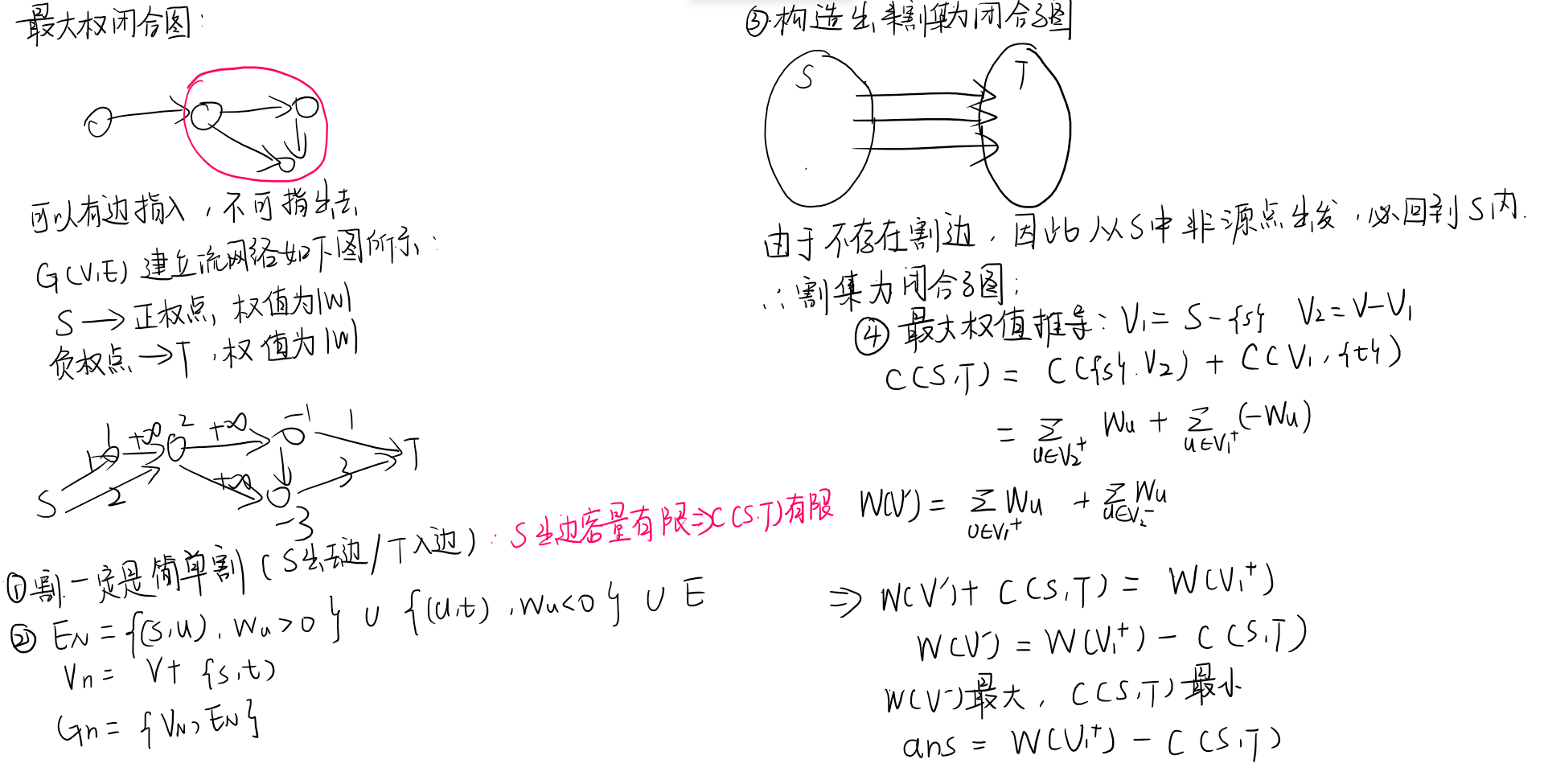
洛谷-最大获利(最大权闭合图解法)
#include <bits/stdc++.h>
using namespace std;
const int N = 55010,M = 5e5 + 10,INF = 1e8;
int h[N],e[M],f[M],ne[M],idx;
int cur[N],q[N],d[N];
int n,m,S,T;
void add(int a,int b,int c)
{
e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
bool bfs()
{
memset(d,-1,sizeof d);
int tt = 0,hh = 0;
q[0] = S,d[S] = 0,cur[S] = h[S];
while(tt>=hh)
{
int t = q[hh++];
for(int i = h[t];~i;i = ne[i])
{
int ver = e[i];
if(d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if(ver == T) return true;
q[++tt] = ver;
}
}
}
return false;
}
int find(int u,int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = h[u];~i&&flow<limit;i = ne[i])
{
cur[u] = i;
int ver = e[i];
if(d[ver] == d[u] + 1 && f[i])
{
int t = find(ver,min(limit-flow,f[i]));
if(!t) d[ver] = -1;
f[i] -= t,f[i^1] += t,flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0,flow;
while(bfs()) while(flow = find(S,INF)) r += flow;
return r;
}
int main()
{
scanf("%d%d",&n,&m);
S = 0,T = n+m+1;
memset(h,-1,sizeof h);
for(int i = 1;i<=n;i++)
{
int x;
scanf("%d",&x);
add(m+i,T,x);
}
int tot = 0;
for(int i = 1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(S,i,c);
add(i,m+a,INF);
add(i,m+b,INF);
tot += c;
}
printf("%d\n",tot - dinic());
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号