5月杂题选做(part1)
上回说到:2022.4
关于难度
\(\color{gray}\bigstar\) 可以秒杀的题。
\(\color{green}\bigstar\) 思考一会儿后可以秒的题。
\(\color{blue}\bigstar\) 需要较长时间思考的题。
\(\color{Gold}\bigstar\) 看题解、稍加指点就会做的题。
\(\color{red}\bigstar\) 看题解后需要较长时间消化,甚至现在都没有完全理解的题。
和 yk,psz 组队打了一场 AT 上的 ACM。比赛链接
赛时 psz 过了 A,yk 过了 B,我过了 EGH,题目质量挺高。
E \(\color{blue}\bigstar\)
已知一张 \(n\) 个点的无向完全图,\(i\) 到 \(j\) 的路径长度为 \(\min(|a_i-a_j|,|b_i-b_j|)\),求所有从 \(1\) 开始的哈密顿回路的路径长度之和。
\(n\le 2\times 10^5\)。
标签:数学。
赛时想了 \(30\) 分钟,好题。
距离很阴间,考虑转化一下,可以发现如果是 \(\max(|a_i-a_j|,|b_i-b_j|)\) 就可以转坐标使得两个独立,所以用 \(\min(a,b)=a+b-\max(a,b)\) 转化,这样就把两维独立了。
考虑独立一位咋做,也就是距离是 \(|a_i-a_j|\) 时的答案。
考虑绝对值展开,一个 \(a_i\) 堆答案的贡献是 \(2a_i,0,2a_i\) 中的一种。
考虑 \(2a_i\) 方案数,也就是从一个小的点走过来,然后再走到一个小的点,可以把这三个点合并成一个,方案数就是 \((i-1)(i-2)(n-3)!\),\(-2a_i\) 同理,算就完了。
G \(\color{green}\bigstar\)
已知序列 \(l,r\),求对于每个 \(k\in[1,m]\),有多少个序列 \(a\) 满足 \(l_i\le a_i\le r_i\) 且 \(\gcd(a_1,a_2...a_n)=k\)
\(n,m,l_i,r_i\le 2\times 10^5\)。
标签:容斥。
套路题,设 \(f_k\) 表示多少个 \(a\) 满足 \(k|\gcd(a_1,a_2..a_n)\),知道这个以后就可以直接容斥算了。
这个东西显然可以直接整除分块然后区间修改做。
赛时比较 sb,用莫比乌斯函数做容斥。
H \(\color{green}\bigstar\)
已知一张 \(n\) 个点 \(m\) 条边的无向联通图,定义 \(f(i,j)\) 表示从 \(i\) 走到 \(j\) ,再从 \(j\) 走到 \(i\) ,重复经过的点的最小值(不包括 \(i\)),求 \(\sum_{l=1}^n \sum_{r=l+1}^n f(l,r)\)。
\(n,m\le 2\times 10^5\)。
标签:圆方树。
简单题,其实本来是看看后面哪题过的人比较多,明明 G 是最多的,手滑开成 H,结果秒了,拿下全场 third AC+shortest code。
考虑两条路径如果不重复经过点,那么一定是在一个点双联通分量中,所以可以先缩点,树上问题考虑进行圆方树统计。
先直接建出,那么 \(f(i,j)\) 就相当于 \(i\) 到 \(j\) 路径上的圆点数量了,可以直接树形 dp 求。
I \(\color{blue}\bigstar\)
题比较长,自己看吧。
标签:容斥。
考虑一个质数对答案的贡献,将相邻的 \(k\) 个分成一组,那么一种方案的贡献就是每组最小值的最大值。
然后可以容斥一下,考虑算贡献 \(\ge x\) 的方案数。
直接容斥,枚举有多少个组满足。
不难理解,就是把满足的和不满足的分别排列然后放进去。
可以 NTT 预处理然后每次查询,不过很阿拉丁,可以发现询问次数 \(O(n\log n)\) 级别,可以直接暴力。
注意上面计算的是一个数的指数,所以模数为 \(10^9+6\),可以分解为 \((5\times 10^8+3)\times 2\),做左边的然后直接 CRT 合并。
J \(\color{green}\bigstar\)
已知一个多项式 \(f(x)=\sum_{i=0}^{10} c_ix^i\),求构造两个序列 \(A,B\),满足两个序列所有数均不相同,且长度 \(\le 5000\),\(A_i,B_i\le 5000\),输出方案。
标签:构造。
显然答案不依赖于 \(c_i\),可以直接构造。
考虑多项式如果只有两项咋做,直接 \(A=\{1,4\},B=\{2,3\}\) 即可。
为了满足 \(x^2\) 项,所以把相邻四个数捆成一组,然后打表出每组 \(x^2\) 项之和,可以发现全部一样,所以可以构造 \(A=\{1,4,6,7\},B=\{2,3,5,8\}\)。
同理打表,可以发现 \(x^3\) 项也满足。
得到构造方法,每次扩展一倍,然后翻转,得到答案。
详细证明可以看 官方题解
ZJOI 没去,太逊了233.
场外选手嘴巴。
Day1T1 \(\color{blue}\bigstar\)
我们构建两棵树,构建方法分别是:
第一棵:根是 \(1\),对于 \([2,n]\) 中的节点 \(i\),向 \([1,i-1]\) 中的一个节点连边。
第二棵:根是 \(n\),对于 \([1,n-1]\) 中的节点 \(i\),向 \([i+1,n]\) 中的一个节点连边。
称一种方案是好的当且仅当对于第一棵树的一个非叶子节点,它是第二棵树的叶子节点;对于第二棵树的非叶子节点,它是第一棵树的叶子节点。
给出 \(n\),对于所有 \(i \in [2, n]\) 回答有 \(i\) 个节点的好的方案有多少,答案对 \(m\) 取模。
\(n\le 500\)。
标签:dp,容斥。
称第一棵中不为叶子的为 \(A\) 类点,第二棵中的为 \(B\) 类点。
可以发现一个点的连边数就是左边的 \(A\) 加上右边的 \(B\)。
但这样会有一个问题,就是分配完了之后,开始钦定的不为叶子的点可能没有点连向它,然后此时就变成了叶子,不合法。
所以容斥一下,计算两边都为叶子的点。
考虑从左向右做,那么前面计算过了两边都计算过的点可以通过左边的 \(A\) 类点,右边的 \(B\) 类点,左边的 \(B\) 类点来求出。
具体来说,设 \(f_{i,a,b_1,b_2}\) 表示 \([1,i]\) 中点的贡献已经计算完了,左边有 \(a\) 个 \(A\) 类点,有 \(b_1\) 个 \(B\) 类点,右边还有 \(b_2\) 个 \(B\) 类点的方案数。
转移很好转移,考虑 \(i+1\) 号点是哪种即可,注意如果选择两边都不放需要乘二,因为既可以容斥掉放在第一棵中的,也可以容斥掉在第二棵中的,时间复杂度 \(O(n^4)\)。
初值为 \(f_{1,1,0,i}=i\)
稍稍卡常后可以获得 \(60\) 分,注意需要使用滚动数组。
然后考虑咋优化,可以发现转移方程和 \(b_1\) 一点关系也没有,\(b_1\) 只与最后的容斥系数有关,所以可以直接把容斥系数加掉计数中去,设 \(f_{i,a,b}\) 即可,直接转移,这样只需要放两边都是叶子的点时改为减即可,时间复杂度 \(O(n^3)\)。
本题超级卡常,需要使用各种玄学优化。
Day1T2 \(\color{blue}\bigstar\)
已知一个序列,可以选择一个区间,把这个区间中的每个数加一个任意的数 \(x\),求操作之后序列众数的最大值,以及有多少个数可能满足成为最大的众数。
\(n\le 2\times 10^5\)。
标签:根号分治。
小清新签到题。
\(O(n^2)\) 很简单,直接确定左端点后右端点左右各扫一遍合并答案即可,另外一种做法是预处理 \(f_{i,j}\) 表示 \(i\) 为左端点,众数为 \(j\) 的区间右端点最小值,然后可以直接暴力枚举区间。
\(O(a_i^2n)\) 也简单,枚举两个数,然后直接前缀和找一下最大值即可,这样 \(40\) 分到手。
然后既然求众数,先想根号,可以发现如果一个数出现次数 \(\ge \sqrt{n}\),可以采用下面的方法直接预处理后查询,如果 \(<\sqrt{n}\) 可以直接用 \(O(n^2)\) 的第二种方法,此时 \(j\) 只需要处理到 \(\sqrt{n}\),因为本质上是查询两个出现次数都少的数。
时间复杂度 \(O(n\sqrt{n})\)。
code luogu AC,loj TLE???
ARC119E *2502 \(\color{green}\bigstar\)
给一个序列 \(a_i\),定义权值为 \(\sum_{i=1}^{n-1}|a_i-a_{i+1}|\),现在可以翻转一个区间,求翻转后权值最小值。
\(n\le 3\times 10^5\)。
标签:贪心。
翻转一个区间,本质也就是交换两个数,改变的只有两边的值。
翻转区间为 \([l,r]\),假设 \(a_{l-1}<a_{r+1}\),大力讨论 \(a_l,a_r\) 的情况,发现只有 \(a_{l-1}<a_l,a_r<a_{r+1}\) 时翻转会更优。
全部都取出来,变成了一个两个区间交集最大问题,排序后维护前缀右端点最大值即可。
需要特判区间一个端点是 \(1,n\) 的情况。
序列倒过来再做一遍就好了。
ARC127C *2092 \(\color{green}\bigstar\)
把 \([1,2^n-1]\) 的数写成二进制,然后按字典序排序,输出第 \(x\) 小的,\(x\) 按二进制给出。
\(n\le 10^6,x< 2^n\)。
标签:模拟(?
考虑先输出一个 \(1\),然后发现后面一位有三种情况,空,\(0,1\)。
那么如果空就结束,如果在 \(0\) 那么 \(x\) 减一,如果在 \(1\) 就去掉头上的 \(1\)。
模拟一遍就好了。
ARC127D *2593 \(\color{blue}\bigstar\)
已知两个长度为 \(n\) 的序列 \(a,b\),求 \(\sum_{1 \leq i<j \leq N} \min \left(A_{i} \oplus A_{j}, B_{i} \oplus B_{j}\right)\)
\(n\le 10^6,a_i,b_i\le 2^{18}\)。
标签:字典树。
想题十分钟,写题两小时,呕。
考虑因为要在 \(a,b\) 中取个小的,可以考虑字典树。
一对 \((a_i,b_i)\) 可以变成一个四进制数,每一位就是 \(a,b\) 的这一位拼起来,这样得到一颗四叉树。
可以发现这样对于一个询问来说,有两个分叉是可以直接统计答案的,有两个是需要继续向下的,复杂度爆炸。
一个简单的想法是既然有两个子树继续向下,那么直接把两棵子树合并为一棵即可。
那么任意两棵子树合并为一棵,有 \(6\) 种方案,加上原来的之后一共 \(10\) 叉数,空间爆炸。
可以发现 \(6\) 中方案中只有 \((00,11),(01,10)\) 是可能继续向下走的,所以变成 \(6\) 叉树,依然爆炸。
想了一会儿,发现我是 sb。因为原来的四叉树是用来直接统计答案的,所以不需要向下了,变成二叉树。
这样就可以了,然后暴力做就完了,时间复杂度 \(O(n\log^2 a_i)\)。
真的阿拉丁,调了两小时。
ARC127E *2678 \(\color{green}\bigstar\)
已知一个长度为 \(A+B\) 的操作序列,序列中只有 \(1,2\),有两种操作:
- 选择一个之前没有出现过的数 \(1\le v\le A\),把它放入一个集合。
- 把集合中最大数删除。
求最后有多少种可能的集合,答案对 \(998244353\) 取模。
\(A\le 5000\)。
标签:dp。
已知 \(B\) 个数,如何判断这些数可以被删除。
最优策略一定是先排序,然后从小到大删除,因为如果不是从小到大必然可以交换一下。
假设这 \(B\) 个数是 \(a_1...a_B\),那么满足 \(a_1\le a_2...\le a_B\)。
然后考虑一个数被删除的条件,可以算出在这个数前有多少个需要放多少个数,那么这个数必须大于等于它,所以可以得到 \(a_i\ge p_i\) 这样的式子。
然后直接 dp,设 \(f_{i,j}\) 表示第 \(i\) 个数放 \(j\) 的方案数,直接前缀和优化就做完了,时间复杂度 \(O(A^2)\)。
打了 AGC057,赛时过了 AB,perf 2417.
AB 其实都不难,B 只有 2000-,但 A 我写了 \(20\) 分钟,B 我写了一个小时。
场上大部分人都做出了 AB,CD 都是铜牌题,AB 过的最快的 Petr perf 3090,用时 \(12\) 分钟。
之前觉得打 AT 比赛就是重在思维,能想出题就可以上分,但这次 AGC 的 D 题我想出了离正解非常接近的做法,但是呢,时间不够,换来的只能是 WA。
我总觉得我迟迟没有上 1 Dan 的原因就是因为比赛打的少,现在看来,我的综合水平可能就是只有 1 Dan 不到。
我无法做到和 EI 或者 apiad 那样强到可以轻松切 AGC EF,所以,从头开始吧。
赛前看到一些 2500+ 的题感觉也可以随便切,但像 ARC127D 那样写两个小时换来的 AC 又有什么意义呢?
开始写 这里 的 difficult 中的题。
AGC057B *1952 \(\color{blue}\bigstar\)
已知一个长度为 \(n\) 的数列 \(a\) 和一个数 \(X\),可以进行若干次操作,每次操作选择一个数 \(a_i\),把 \(a_i\) 修改为 \(2a_i+x\),其中 \(x\) 为 \(\le X\) 的任意非负整数,求操作后 \(\max a_i-\min a_i\) 的最小值。
\(n\le 10^5,a_i\le 10^9\)。
标签:贪心,单调队列,线段树。
考虑如果对一个数 \(A\) 进行 \(k\) 次操作,那么就会变成 \(2...2(2(2A+x_1)+x_2)+x_3)+...x_k=2^kA+2^{k-1}x_1+2^{k-2}x_2...+x_k\) 的形式。
可以发现,由于 \(0\le x_i\le X\) 可以任意取值,所以通过二进制相关知识可以发现可以取出 \([2^kA,2^kA+(2^k-1)X]\) 中的所有的数。
可以发现 \(k\) 的取值不可能很大,只有 \(\log a_i\) 级别,所以可以暴力取出所有区间。
问题转化成一个有一堆区间,每个区间有一个编号,求一个最小的区间满足与每个编号的区间都有交集。
按左端点排序,然后扫一遍,答案就是最大左端点减去最小右端点,显然每个编号只保留最后一个,可以单调队列维护,也可以直接线段树。
注意这个题一个编号产生的区间互相没有包含关系,所以这个做法是对的,否则还需要把包含的小区间去掉
ARC110D *2078 \(\color{green}\bigstar\)
已知一个长度为 \(n\) 的序列 \(a\) 和一个数 \(M\),求对于所有 \(\sum b_i\le M\) 的序列 \(b\),\(\prod \binom{b_i}{a_i}\) 的和,答案对 \(10^9+7\) 取模。
\(n,a_i\le 2000,M\le 10^9\)。
简单组合意义题。
考虑先选 \(a_1\),再选 \(a_2\),一直选下去,由于 \(\sum b_i\le M\),所以可以把问题变为有 \(M\) 个球的染色问题,然 \(a_1\) 个 \(1\),\(a_2\) 个 \(2\),那么首先要求位置连续,也就是 \(i\) 的球必须在 \(i+1\) 的前面,令 \(s=\sum a_i\),那么这样染色的方案数是 \(\binom{M}{s}\)。
但会有一个问题,对于一种染色方案有多种 \(b_i\) 的取值,比如对于 \(...100002....\) 这样的染色方案,\(b_1\) 可以选 \(1\) 到 \(2\) 中间的任意一个位置。
那么就加 \(n\) 个球用来放 \(b\),然后再扔掉即可,所以最后的答案就是 \(\binom{M+n}{s+n}\)。
ABC191F *2333 \(\color{green}\bigstar\)
有 \(n\) 个数,每次操作选择两个数 \(a_i,a_j\),把它们删除,并把 \(\min(a_i,a_j)\) 或者 \(\gcd(a_i,a_j)\) 放回原序列,求最后剩下一个数,这个数的可能情况。
\(n\le 2000,a_i\le 10^9\)。
首先可以发现 \(\gcd(a,b)<\min(a,b)\),所以最后剩下的数一定 \(\le \min(a_i)\),所以容易发现,问题变成选任意多个数,它们取 \(\gcd\),然后在与剩下的数取 \(\min\)。
考虑如何判断一个数是否合法,首先需要 \(\le \min(a_i)\),直接把它的倍数全部拿出来取 \(\gcd\) 看是否满足等于自己即可。
然后直接对每个数分解后暴力做就好了。
时间复杂度 \(O(n\sqrt{a_i})\)。
AGC038C *2327 \(\color{green}\bigstar\)
已知一个数列 \(a_i\),求 \(\sum_{1\le i<j\le n}lcm(a_i,a_j)\) 对 \(998244353\) 取模。
\(n\le 2\times 10^5,a_i\le 10^6\)。
标签:莫反。
双倍经验。
简单莫反题。
令 \(c_i\) 表示 \(i\) 的出现次数,那么
可以发现直接计算 \(\sum_{i=1}^n \sum_{j=1}^n \frac{c_ic_jij}{\gcd(i,j)}\),即可,因为答案直接减去相同的再除以 \(2\) 即可。
这样直接做是 \(O(a_i\log^2 a_i)\),貌似能过。
可以优化,可以设 \(T=dp\)。
左边是一个狄利克雷卷积,直接预处理就好了,时间复杂度 \(O(n\log n)\)。
ABC147F *2393 \(\color{blue}\bigstar\)
有一个长度为 \(n\) 的序列满足 \(a_1=X,a_i=a_{i-1}+D\),现在可以给每个数乘上 \(1\) 或 \(-1\),然后求此时的和的可能方案数。
\(n\le 2\times 10^5,X,D\le 10^8\)。
不是很难,但很阿拉丁,我吃了 \(6\) 发 WA。
考虑把和加 \(\sum a_i\) 然后再除以 \(2\) 之后 \(1\) 变成了 \(1\),\(-1\) 变成了 \(0\),所以只需要考虑选那些数就好了。
选的数可以发现分成 \(X\) 和 \(D\) 两部分。
枚举一下选多少个数就可以确定 \(X\) 部分,按 \(X\mod D\) 进行分类,然后可以 \(D\) 部分是一个区间,直接区间求并就完了。
code。
ARC112C *1913 \(\color{blue}\bigstar\)
双人在树上博弈,每个节点一个金币,\(1\) 号点初始有一个棋子,每次操作可以拿走棋子所在位置的金币,或者把棋子移到一个没去过的儿子节点,或者返回叶子节点,每人使用最优策略是自己金币最多,求最后先手有多少金币。
\(n\le 10^5\)。
显然树形 dp,设 \(f_i\) 表示 \(i\) 子树做完之后先手比后手多多少。
考虑每个儿子,如果儿子子树大小为偶数,那么相互之间没有影响,那么如果有负数后手必然贪心全部选。
如果是奇数,那么就排序,双方轮流取最小的来恶心对方。
最后全部偶数正数之和是个最没用的,最后的人不得不取。
然后直接做就好了。
ARC122D *2331 \(\color{blue}\bigstar\)
已知 \(2n\) 个数,先手后手轮流取数,最后的得分是每轮双方得分的异或的最大值,先手想让答案尽量大,后手想让答案尽量小,求最后的得分。
\(n\le 2\times 10^5,a_i\le 2^{30}\)。
标签:字典树,二分。
字典树题,我只能说呕。
可以二分答案一下,容易发现后手最优策略就是对所有数进行两两匹配,然后先手取一个后手就取另一个,问题转化为两两匹配得分最小值。
找到二分值的最高位 \(1\) 所在层的点,如果两个儿子都是偶数那么可以自己匹配,合法,如果一奇一偶那么必然无法,如果两个奇数那么就在两棵子树里面找最小值即可。
时间复杂度 \(O(n\log^2 n)\)
好像不需要二分,可以直接找最小值。
ARC131C *1162 \(\color{blue}\bigstar\)
有 \(n\) 个数,两人博弈,每次选一个数扔掉,如果扔掉后剩下数的异或和为 \(0\) 就赢,求先手是否必胜。
\(n\le 400000\)。
标签:博弈论。
*1200- 想半天,我该怎么办???
考虑如果先手能一下就赢那么结束,否则奇数就先手赢,不然后手赢。
考虑奇数情况,如果一下不合法,然后对面操作一下赢了,假设操作的两个数是 \(a,b\),所有数的异或和是 \(x\),\(a\) 与 \(b\) 异或就是 \(x\),由于 \(a,b\) 都不能等于 \(x\),因为等于就可以一步结束了,那么说明 \(a,b\) 两两对应,必然有一个没有对应,直接选哪个就好了。
ABC250G *2219 \(\color{green}\bigstar\)
一支股票,第 \(i\) 天价格为 \(a_i\) 元,初始钱无限,每天可以选择买入一股,卖出一股,或者什么也不干,求最大利润。
\(n\le 2\times 10^5\)。
标签:贪心。
反悔贪心典中典,直接贪心选前面的就好了,然后再把自己塞入就好了。
ABC250Ex *2773 \(\color{Gold}\bigstar\)
有 \(n\) 个点,\(m\) 条边,其中 \([1..k]\) 位置上可以睡觉,走过每条边需要一定时间,有 \(Q\) 次询问,每次询问两个点以及一个 \(T\),问睡醒后最多走 \(T\) 时间,是否可以从一个点走到另一个。
\(n,m,Q,k\le 2\times 10^5\)。
标签:最小生成树,最短路。
考虑如果 \(k=n\),那么显然是一个最小生成树。
否则考虑如果一条边可以连,需要满足 \(d_x+d_y+z\le T\),\(z\) 表示边权,\(d_x\) 表示 \(x\) 离可以睡觉的点的最短距离,然后离线下来跑最小生成树就好了。
ARC131D *2271 \(\color{green}\bigstar\)
题比较长,自己看吧。
标签:贪心。
显然选的点距离恰好为 \(D\),因为越靠近中间的越优。
分成左右两个部分,那么两个部分选的点数量之差不超过 \(1\),可以算出。
然后对于每个 \(0\le i\le D\),求出第一个点在 \(i\) 的最大值,直接双指针和差分维护即可。
ARC130D *2437 \(\color{green}\bigstar\)
给一棵 \(n\) 个点的树,给树上每个点赋一个点权,满足赋的点权是一个排列,并且对于 \(x\) 的两个相邻的点 \(y,z\),满足 \(a_y<a_x>a_z\) 或者 \(a_y>a_x<a_z\),求有多少种赋值方案,答案对 \(998244353\) 取模。
\(n\le 3000\)。
标签:树形 dp。
首先可以给每个点黑白染色,表示比边上点大还是小。
可以发现两种染色方案方案数相同,所以只需要算一个。
设 \(f_{i,j}\) 表示 \(i\) 为根,\(a_i\) 小于它的儿子,第 \(i\) 个点的权值是第 \(j\) 小的方案数。
那么直接枚举儿子状态,然后考虑有多少个点比 \(i\) 小就可以直接转移,然后类似于树上背包直接做就好了,时间复杂度 \(O(n^2)\)。
注意向上转移需要翻转数组。
ARC134D *1998 \(\color{green}\bigstar\)
有一个长度为 \(2n\) 的数组 \(a\),可以选择一下标 \(1\le p_1,p_2...p_k\le n\),然后组成序列 \(a_{p_1},a_{p_2}...a_{p_k},a_{p_1+n}...a_{p_k+n}\),求这个序列字典序最小是多少。
\(n\le 10^5\)。
标签:贪心。
显然,我们需要找 \(a_{p_i}\) 最小的那个,然后如果 \(a_{p_i+n}<a_{p_i}\),那么答案显然输出这两个数即可。
否则,假设第一元素最小的是 \(x\),然后第一次出现位置的第二个元素是 \(y\),那么单调栈维护第一元素 \([x,y]\) 的序列。
然后接下来考虑,是否可以删除第一元素为 \(y\) 的是否可以删去,找 \(y\) 后面第一个不等于 \(y\) 的,看他大于还是小于 \(y\) 即可。
AGC020C *2259 \(\color{green}\bigstar\)
已知 \(n\) 个数,你需要从中选出任意个数,价值是选出数之和,求对于所有选数方案价值的中位数。
\(n\le 2000,a_i\le 2000\)。
标签:dp。
考虑中位数,相当于小于和大于的数相同,那么对于一个小于 \(mid\) 的数 \(x\),如果记所有数之和为 \(s\),那么也必然存在一个 \(s-x\),这样形成了一一对应,所以相当于求可以凑出那些数。
用 bitset 维护 dp,直接找可以凑出的最中间那个即可,时间复杂度 \(O(\frac{n^3}{w})\)。
tenka12017D *1789 \(\color{Gold}\bigstar\)
已知 \(n\) 组数 \((a_i,b_i)\) 和一个数 \(k\),选出一些数,使得 \(a_i\) 的按位或之和 \(\le k\),\(b_i\) 之和的最大值。
\(n\le 10^5,a_i\le 2^{30}\)。
标签:模拟。
sb 题做不出来,记录每一个降智瞬间。
考虑如果 \(a_i\le 2^{20}\),那么直接暴力 FWT 即可,但会寄。
考虑相当于每个 \(x\le k\),求 \(\sum_{a_i\in x} b_i\) 的最大值,那么 \(x\) 可以从 \(k\) 开始不断减一,然后发现可能对答案有贡献的就是每次找没有遍历过的最低位的 \(1\),然后把它减一,把它前面的全部修改为 \(1\),找最大值即可。
tenka12018E *2459 \(\color{green}\bigstar\)
有一个 \(n\times m\) 的 \(01\) 矩阵,求有多少个三顶点都是 \(1\) 的三角形满足三个点两两曼哈顿距离相等。
\(n\le 300\)。
标签:模拟。
感觉难度有点虚高。。
考虑对于选出的一个三角形,钦定有一个点在右下角,可以旋转 \(4\) 次得到总答案,那么最后的三角形像这样:
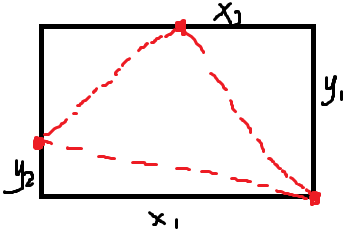
此时 \(x_1+y_2=x_2+y_1=x_1-x_2+y_1-y_2\) 容易发现此时 \(y_1-y_2=x_1-x_2\),也就是左上角两个点在一条对角线上。
然后就可以对于一条对角线,暴力枚举两个点,然后统计右下角点的方案数。
这个方案可以预处理,设 \(f_{i,j,k}\) 表示 \((i,j)\) 为左上角,曼哈顿距离为 \(k\) 的右下角的点有多少个。
可以直接二分找,时间复杂度 \(O(n^3\log n)\),会被卡常。
实际上可以递推,\(f_{i,j,0}\) 可以直接做。
然后直接做就好了,注意会有重复的情况,讨论一下减去即可。
时间复杂度 \(O(n^3)\)。
ARC092E *2361 \(\color{green}\bigstar\)
有一个长度为 \(n\) 的序列 \(a\),有两种操作:
选择一个两端的数,把它删除。
选择一个中间的数 \(a_i\),把 \(a_{i-1},a_i,a_{i+1}\) 合并为一个数 \(a_{i-1}+a_{i+1}\)。
如果只剩下一个数,那么停止操作。
求剩下这个数的最大值,并构造方案。
\(n\le 1000,|a_i|\le 10^9\)。
标签:贪心。
超级诈骗题,绷不住了。
看到 \(n\le 1000\) 先写了半天区间 dp,然后寄了。
考虑最后剩下的数一定是原序列一些数的和,考虑一个子序列如果能被留下,那么必然相邻两个元素中间的一段区间都变成一个数,变成一个数的条件是长度为奇数,具体而言,选出子序列的位置为 \(p_1,p_2...p_k\),那么满足 \(p_{i+1}-p_i-1\) 是奇数。
然后可以直接贪,要么选奇数位置上的正数,要么选偶数位置上的,直接输出方案即可。
注意需要特判全部是负数的情况,时间复杂度 \(O(n)\)。
ABC251Ex *3108 \(\color{blue}\bigstar\)
有一个 \(n\) 行的三角形,第 \(i\) 行有 \(i\) 个数,把第 \(n\) 行的所有数以区间压缩的形式告诉你,如果有一段区间 满足 \(l\le i\le r,a_i=x\),那么就压缩为 \((r-l+1,x)\) 的形式,现在已知有这样的 \(m\) 个区间,让 \(f_{i,j}\) 表示第 \(i\) 行第 \(j\) 个数,满足 \(f_{i,j}=(f_{i+1,j}+f_{i+1,j+1})\mod 7\),求第 \(k\) 行所有的数。
\(n\le 10^9,m\le 200,k\le 5\times 10^5\)。
这个数据范围明示 \(O(mk)\)。。。
先考虑这个递推的过程,容易发现和杨辉三角类似,容易得到:
然后考虑一段区间对答案的贡献,容易发现如果已知对 \(f_{k,1}\) 的贡献,对后面的贡献相当于是平移一格,可以通过加一减一来做,所以直接考虑求 \(f_{k,1}\)。
可以发现本质上是组合数前缀和,模数很小,可以考虑 Lucas 后用分治解决,记录一个 \(\sum_{i=0}^{r-1} \binom{n-k}{i}\) 和 \(\binom{n-k}{r}\) 就可以转移了。
然后考虑向后递推,可以发现本质上求两个长度为 \(k\) 的组合数区间。
由于模数很小,不能用求出一个之后递推的方式来求,所以还是要分治。
然后直接做就好了。
work 函数是贺的,是分治处理组合数区间。
ARC115D *2325 \(\color{Gold}\bigstar\)
有一张 \(n\) 个点,\(m\) 条边的无向连通图,对于每个 \(1\le k\le n\),求有多少个生成子图满足度数是奇数的点的数量为 \(k\)。
\(n,m\le 5000\)。
标签:计数,dp。
不会做,我是不是可以退役了\kk。
考虑如果存在环,那么可以把环上的一条边去掉,然后答案乘以 \(2\),因为环上其他点加起来和这条边等价。所以此时变成了有一堆树的问题。
容易发现一棵树的奇点的数量一定是偶数,并且对于任意选择这些奇点的方案,都有一种满足条件的联通子图,因为只需要进行两两匹配,然后直接把两者之间所有边全部异或 \(1\),(\(1\) 表示选这条边, \(0\) 表示不选)。
因此变成简单的计数 dp 了,记录 \(f_{i,j}\) 表示对于前 \(i\) 棵树,选了 \(j\) 个奇点的方案数,组合数随便转移一下就好了。
打了ARC140,过了 ABC,perf 2259,太逊了,可喜可贺的是终于苟上 1 Dan 了。
极度降智,A 一个傻逼错误结果以为是算法炸了,调了 \(15\) 分钟,BC 都是一眼会了,结果代码写半天,\(43\) 分钟才过 C。
然后做出 sb 决定,我觉得 D 计数不太可做,直接冲貌似挺可做的 E 构造。
结果到最后也没有翻盘,拉垮了,赛后发现 D 是简单题。
看来数树才是我的强项啊,构造这种东西还是留给 psz2007 这种罕见吧。
ARC140D *2443 \(\color{blue}\bigstar\)
已知 \(n\) 个点,第 \(i\) 个点与 \(a_{i}\) 连边,有一些 \(a_i\) 是 \(-1\),需要任意给其附上一个 \([1,n]\) 的权值,求对于所有赋值方案,该图连通块个数之和是多少,答案对 \(998244353\) 取模。
\(n\le 2000\)。
标签:斯特林数,计数,容斥,dp。
考虑最后的图一定是一个基环树森林,先把已知的边连起来,得到一堆连通块,这些连通块要么一个 \(-1\) 都没有,要么含有一个 \(-1\),设 \(p_i\) 表示第 \(i\) 个连通块的大小,本质上相当于缩点了。
考虑既然是基环树森林,那么连通块个数等于环数,考虑哪些点在环上,这些点对答案的贡献是 \(\prod a_i\),其他点的贡献是 \(n\),先进行一下 dp 求出 \(f_i\) 表示钦定 \(i\) 个点在环上的贡献。
接下来考虑容斥,考虑一种 \(j\) 个点在环上的贡献在 \(i\) 中会算多少次。
显然是先选出 \(i\) 个点,然后把剩下的点变成任意的环,所以可以得到算的次数是 \(\binom{j}{i}(j-i)!=\frac{j!}{i!}\),所以容斥相当于 \(f_{i}=f_i-(i+1)f_{i+1}\)。
还有一种更加简单的凑法,容易得到一行第一类斯特林数之和为 \(n!\),考虑假设变换为 \(f_i=f_i-a_{i+1}f_{i+1}\),那么可以得到
显然 \(a_{i+1}=i+1\)。
问题变成有 \(i\) 个点,分配到 \(j\) 个环上的方案数。
经典第一类斯特林数,直接可以得到有 \(i\) 个环的方案数,直接统计答案即可。
** lyc jc 我,把模数改成了 \(99824453\),我调了好久。
std 做法更加简单一些,考虑设 \(g_i=(i-1)!f_i\),这样 \(j\) 个点在环上的贡献在 \(g_i\) 中计算了 \(\frac{j!}{i}\) 次。
考虑一种 \(j\) 对答案的贡献就是
证明:考虑在 \(j\) 个点里面选出一个环,先选出 \(i\) 个点,这 \(i\) 个点形成一个环的方案数是圆排列,然后剩下的可以随便搞,所以得到:
所以只需要把全部 \(g_i\) 加起来就好了,这样就不需要斯特林数了。
ARC071F *2336 \(\color{green}\bigstar\)
已知一个数 \(n\),求有多少个无限长数列 \(a\),满足以下条件:
- 对于 \(n\le i,j,a_i=a_j\)。
- 对于所有 \(a_i,i<j<k\le i+a_i\) 满足 \(a_j=a_k\)。
\(n\le 10^6\)。
标签:dp。
考虑 dp,从后向前做,设 \(f_i\) 表示 \(i\) 后面的答案。
如果 \(a_i>1,a_{i+1}>1\),可以发现后面整个序列都确定了,这个地方贡献为 \((n-1)^2\)。
如果 \(a_i=1\),贡献显然是 \(f_{i+1}\)。
如果 \(a_i>1,a_{i+1}=1\),那么答案显然就是 \(\sum_{j=i+3}^n f_{j}\)。
也有一种可能 \(i+a_i>n\),贡献为 \(i+1\)。
全部加起来,做完了,需要特判 \(a_{n-1}=n^2\)。
keyence2019E *2623 \(\color{Gold}\bigstar\)
已知 \(n\) 个点的无向完全图,\((i,j)\) 边权为 \(|i-j|D+a_i+a_j\),求最小生成树。
\(n\le 10^5\)。
标签:分治,贪心。
比较妙的题,至少我不会做。
考虑把序列分成前面一半和后面一半,这样前面的点 \(i\) 到后面的点 \(j\) 的代价就死 \(a_i-iD+a_j+jD\),这样就可以在前面和后面分别找最小值,然后可以发现越过中间的边一定都是连向 \(i\) 的边或者是连向 \(j\) 的边,因为如果另外存在一条 \((i_0,j_0)\),那么显然 \((i_0,j),(i,j_0),(i,j)\) 三条边都比 \((i_0,j_0)\) 小。
所以直接这样分治,然后暴力连边,直接跑最小生成树,边数是 \(O(n\log n)\) 级别的,总时间复杂度 \(O(n\log^2 n)\)。
有一个更加牛的 \(O(n)\) 做法,我是看也看不懂,放个 代码 ,有没有老哥解释一下咋做啊。
ABC219G *2287 \(\color{green}\bigstar\)
已知一张 \(n\) 个点的图,初始时第 \(i\) 个点的颜色是 \(i\),有 \(Q\) 次操作,每次操作选择一个点,然后把和这个点直接相连的点的颜色全部改为这个点的颜色,求最后所有点的颜色。
\(n,Q\le 2\times 10^5\)。
标签:根号分治。
根号分治一下,如果一个点度数小于 \(\sqrt{n}\),那么可以直接暴力修改即可,否则考虑标记一下这个点,那么询问一个点的答案是只需要询问与这个点相邻的度数 \(>\sqrt{n}\) 的点即可。
ARC073E *2434 \(\color{blue}\bigstar\)
有 \(n\) 组球,每组两个球,现在把球放到两个盒子里面,一组在两个盒子里面各放一个,每个球上有一个数字,求最后两个盒子极差之积的最小值。
\(n\le 2\times 10^5\)。
标签:贪心。
考虑先把所有球从小到大排序,分两种情况讨论。
- 最小的球和最大的球在同一个盒子里。
此时需要先保证这两个球不在同一组,那么相当于接下来每组选一个数,然后使得极差最小,这个可以直接双指针扫一遍就好了。
- 最小的球和最大的球不在同一个盒子里。
此时一个盒子的最小值确定,另一个的最大值确定,那么对于每组显然是小的全部放一个盒子里,大的全部放另一个。
yahooprocon2019qualE *2434 \(\color{Gold}\bigstar\)
已知一个 \(n\times m\) 的矩阵,每个位置要么是黑的,要么是白的,选择一个问有多少个子矩阵满足有奇数个黑点,答案对 \(998244353\) 取模。
此处子矩阵指对于两个长度分别为 \(n,m\) 子序列 \(p,q\),所有 \(i\in p,j\in q,a_{i,j}\) 所构成的矩阵。
\(n,m\le 300\)。
标签:线性基。
牛子计数题,根本不会做。
考虑如果确定了取那些行,那么相当于每一个列有一些黑色点,假设有 \(x\) 个列有偶数个黑色点,有 \(y\) 个列的奇数个黑色点,那么如果 \(y=0\) 显然方案数是 \(0\),否则可以选择一个奇数列,那么对于其他所有方案,只需要这个选或者不选就可以进行一一对应,所以相当于奇偶方案一样,总方案数就是 \(2^{m-1}\)。
然后再去考虑选行,选出一些行使得这些行的异或和不是 \(0\)。
先建立一个线性基,考虑直接去算等于 \(0\) 的答案。
考虑对于线性基外的每种选行方案,线性基中都对应着唯一一种的方案使得异或和是 \(0\)。
假设线性基中有 \(k\) 个元素,那么最后的答案就是 \(2^{m-1}(2^n-2^{n-k})\)。
vp 了 Code Festival 2016 Grand Final,过了 ACDG,完全被榜带偏,菜爆了。
A \(\color{gray}\bigstar\)
已知两个长度为 \(n\) 的数组 \(a,b\),需要把 \(a\) 与 \(b\) 中的数进行匹配,两个数匹配的代价是两者之差,求让总代价之和最小的方案数。
\(n\le 10^5\)。
标签:模拟,计数。
考虑如果求最小咋做,就是直接对两个排序然后一一匹配即可。
然后考虑计数,先把两个数组放到一起排序,那么对于一个数必然是找在它之前的任意一个没有被匹配的,和它不是在一个数组里的数,直接统计即可。
C \(\color{gray}\bigstar\)
有 \(n\) 堆石子,两个人玩 nim 游戏,先手可以在开始前选择一些堆,把这些堆石子个数减一,问是否有一种必胜策略。
\(n\le 10^5\)。
标签:模拟。
先转化为异或问题,可以发现减一实际上就是把最低位换成后面全是 \(1\),因此从高到底考虑每一位,如果这位不满足就减一,然后判断是否合法即可。
D \(\color{blue}\bigstar\)
有两个六面骰子,把每个骰子每个面的概率已知,现在有两个人游戏,第一个人选择一个骰子扔出,告诉第二个人点数,第二个人猜,猜对则第二个人胜,求第二个人胜率。
标签:三分,贪心。
一开始有个很简单的贪心:考虑哪个骰子的胜率大就扔哪个,但是会寄。
事实上,第一个人的策略是给两个骰子分配选中的概率,假设选中第一个的概率是 \(p\),那么胜率 \(f(p)\) 显然可以三分求极值。
考虑胜率咋求,投中一个点数 \(i\) 的概率就是 \(a_ip+b_i(1-p)\),开始有一个很简单的想法,就是第二个人选 \(a_i,b_i\) 中大的那个骰子。
但是这样还是会寄,因为第二个人是知道骰子的概率的,所以它可以预判第一个人的策略,所以它选择的是 \(a_ip,b_i(1-p)\) 中大的那个,然后直接做就好了。
J \(\color{Gold}\bigstar\)
\(1..2n\) ,对这些数两两匹配,然后使得有 \(a\) 组差为 \(1\),\(b\) 组差为 \(2\),\(c\) 组差为 \(3\)。
\(n\le 5000\)。
标签:计数。
直接暴力看有哪些方式可以搞出一个连通块,只有 \(aa,baab,abab\) 等几种情况,暴力枚举就好了。
codefestival_2016_qualC_D *2283 \(\color{green}\bigstar\)
有 \(n\times m\) 的矩阵,每个格子有一个颜色,每次操作可以选择一列向下移动一个,把最下面一个销毁掉,代价为操作前这一列与相邻列有多少个位置颜色相同,求把所有销毁的最小代价。
\(n,m\le 300\)。
标签:dp。
显然,对于每相邻两列来说都是相对独立的,所以可以对所有相邻两列统计答案然后加起来。
显然 dp,\(f_{i,j}\) 表示第一列高度为 \(i\),第二列高度为 \(j\) 的最小代价,然后计算代价只需要直接类似前缀和预处理一下就好了。
发现每次 ARC 都是 D 做不出来,所以板刷。
ARC104D *2251 \(\color{blue}\bigstar\)
已知 \(n,m,k\),对于每个 \(1\le x\le n\) 求出,有多少个只含有含 \(1..n\),每个数出现次数 \(\le k\) 的,集合中数的平均数等于 \(x\) 的可重集数量,答案对 \(m\) 取模。
\(n,k\le 100\)。
标签:背包,dp。
考虑先枚举一个 \(x\),然后考虑选其他数,那么可以看成是有 \(-x+1,-x+2...-1,1,2,3...n-x\),这些体积的物品各 \(k\) 个,求选出体积为 \(0\) 的物品的方案数。
可以设 \(f_{i,j}\) 表示 \(1..i\) 的物品,放入 \(j\) 的体积的方案数。
相当于多重背包求方案数,不能二进制分组,暴力做会炸。
考虑这样一个东西,放一个物品是 \(f_{i,j}+=f_{i-1,j-i}\),两个就是 \(f_{i-1,j-2*i}\),所以最后的式子是 \(f_{i,j}=\sum_{p=1}^k f_{i-1,j-p*i}\)。
转化一下。
如果不考虑做后面减去的,那么显然是一个完全背包,但有后面的,可以发现完全背包相当于一个前缀和,直接减去后面的即可。
然后统计答案直接判正负的体积相等即可。
ARC105D *1871 \(\color{Gold}\bigstar\)
两人博弈,一开始有 \(n\) 袋石子,每袋 \(a_i\) 个,有 \(n\) 个空盘子,先手后手轮流选择一袋石子放到任意一个盘子上,然后玩 nim 游戏,问先手是否有必胜策略。
\(n\le 10^5\)。
标签:博弈。
sb 了,简单题不会做。
先考虑 \(n\) 的奇偶性会影响玩 nim 游戏的先后手操作,那么分情况讨论。
如果 \(n\) 为偶数,那么显然先手一直选最大的放到一个盘子里,这样得到的一个盘子一定大于其他所有的,有一种特殊情况是恰好等于,也就是相等的数可以两两匹配,特判一下。
然后不会了。
考虑 \(n\) 为奇数,那么后手采用类似的思路,先手一开始选一个放在一个盘子里,后手就每次选最大的那个放在这个盘子里,后手必胜。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号