前言:考场上使用神秘的样例分析法蒙出来了,赛后发现竟然被评了个紫,万恶的良心驱使我写一篇题解。
我们先看到操作。
- 任选一个数字使其 \(+2\)
- 选择两个相邻的数字使其各 \(+1\)
要求 使用操作 \(2\) 的次数最小。
换句话说我们可以任意使用操作 \(1\) 。
这启发我们进行 奇偶性分析。
对于一个奇数 \(n\) , \(1-n\) 的排列中奇数的个数为 \(\frac{n+1}{2}\) 。令其等于 \(k\) .
我们对于一个排列\(\pi\),构造它 \(\bmod 2\) 意义下的数列 \(b\)
\[(\pi_1 \bmod 2,\pi_2 \bmod 2,...\pi_n \bmod 2 )
\]
我们不妨称此为一次映射。
对于一组 \(b\) ,在所有排列中由此映射到这个 \(b\) 的个数都是
\[k!\times (n-k)!
\]
事实上,我们发现,对于映射后序列相同的所有排列,其答案必然相等。
我们记 \(S_b\) 表示 \(b\) 中为 \(1\) 的位置的下标的集合。显而易见 \(|S_b| = k\)
我真没在骂人
记 \(m(S_b)\) 表示 \(S_b\) 这个代表的所有排列的答案。
则
\[ans= k!(n-k)! \sum_{|S_b|=k}m(S_b)
\]
记 \(C=(^n_k)\),则
\[ans=n!\frac{1}{C} \sum_{|S_b|=k}m(S_b)
\]
此时问题转化为如何求这个操作次数。
- 给定一个奇偶向量 \(b=(b1,\dots,b_n)\)
我们将 操作转化为线性方程
把在第 \(i\) 条边(即连接顶点 i 与 i+1 )所做操作 (2) 的次数记为整数 \(x_i\ge0\) \((i=1,\dots,n-1)\)。
每次操作在两个相邻位置同时 +1,因此只改变这两个位置的奇偶(翻转)。
若我们只关心 模 2 的奇偶,则每个顶点的最终奇偶等式为(以目标统一成常数 \(t\in{{0,1}}\),表示我们要把全部数变成偶或全部变成奇):
\[ x_{i-1}+x_i \equiv b_i + t \pmod 2\quad (i=1,\dots,n),
\]
其中约定 \(x_0=x_n=0\).
你现在发现这个 \(t\) 很烦人。我们随机手算一下样例会发现这个 \(t\) 其实是 唯一确定的 !
考虑由 GPT 提供的证明。
将 RHS 总和求和得到
\[\sum_{i=1}^n(b_i+t)=\sum b_i +nt=k+nt
\]
左式 必定为偶数,因此 \(t\) 与 \(k\) 同奇偶
\[\square
\]
表示方程。
\[x_{i-1}+x_i \equiv b_i+t(\bmod 2)
\]
以 \(x_0=0\) 开始递推,可得:
\[ x_1 \equiv b_1 + t,
\]
\[ x_2 \equiv b_2 + t + x_1 \equiv (b_1+b_2) + (2t) \equiv (b_1+b_2) + 0 \pmod2,
\]
更一般地,使用异或表示
\[x_i = \bigoplus_{j=1}^i (b_j \oplus t),
\]
记
\[s_i=\sum_{j=1}^i b_j (0\le s_i\le i)
\]
因为 \(t\) 为常数,所以
\[x_i=s_i \bmod 2 \oplus (i\ · \ t\bmod 2)=(s_i \bmod 2) \oplus ((i·t) \bmod 2)
\]
因此
\[m(S)=\sum_{i=1}^{n-1} x_i
= \#[1\le i\le n-1: \ s_i \bmod 2 \ne (i\cdot t)\bmod 2]\]
我们要计算
\[\sum_{|S|=k} m(S)
=\sum_{|S|=k} \sum_{i=1}^{n-1} \mathbf 1{ s_i \bmod 2 \ne (i t)\bmod 2}\]
\[=\sum_{i=1}^{n-1} \# \Big{ S: |S|=k,\ s_i \bmod 2 \ne (i t)\bmod 2\Big}}
\]
好吧这里的 latex 寄了
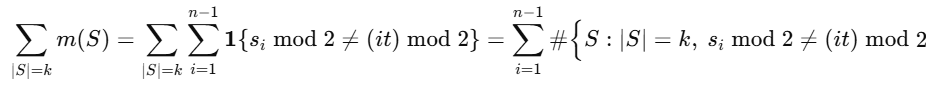
固定 \(i\) 。把前 \(i\) 个位置中恰好有 \(u\) 个 \(1\) \((0\le u\le\min(i,k))\)
\[\# \{S:s_i=u,|S|=k\}=\binom{i}{u} \binom{n-i}{k-u}
\]
于是,前缀 (s_i) 的奇偶分布为:奇数的个数
\[ O_i=\sum_{\substack{0\le u\le\min(i,k)\ u\ \text{odd}}}\binom{i}{u}\binom{n-i}{k-u},
\]
偶数的个数
\[E_i=\sum_{u\ \text{even}}\binom{i}{u}\binom{n-i}{k-u}
\]
总数
\[(E_i+O_i=\binom{n}{k}=\mathcal C).
\]
我们定义
\[D_i = E_i - O_i
= \sum_{u}(-1)^u \binom{i}{u}\binom{n-i}{k-u}\]
使用
\[E_i=(\mathcal C+D_i)/2, O_i=(\mathcal C-D_i)/2
\]
则有
\[\# \{S:s_i=u,|S|=k\}=\frac{\mathcal C-(-1)^{it}D_i}{2}
\]
因此
\[\sum_{|S|=k} m(S)
= \sum_{i=1}^{n-1} \frac{\mathcal C - (-1)^{it} D_i}{2}
= \frac{n-1}{2}\mathcal C - \frac{1}{2}\sum_{i=1}^{n-1} (-1)^{it} D_i.\]
于是平均值
\[\overline m(n) = \frac{1}{\mathcal C}\sum_{|S|=k} m(S)
= \frac{n-1}{2} - \frac{1}{2\mathcal C}\sum_{i=1}^{n-1} (-1)^{it} D_i.
\tag{★}\]
下面是牛逼的生成函数,但是是 GPT 写的(x)
其实到这个时候是可以自己手动猜测 \(D\) 了。式子在下面。我建议大家跳过 GPT 写的这一坨 shi
接下来的核心工作就是计算
\[\mathcal D:=\sum_{i=1}^{n-1} (-1)^{i t} D_i
=\sum_{i=1}^{n-1} (-1)^{i t}\sum_{u}(-1)^u\binom{i}{u}\binom{n-i}{k-u}.\]
将 \(D_i\) 看成系数,对于任意的 \(i\)
\[D_i=\sum_{u}(-1)^u\binom{i}{u}\binom{n-i}{k-u}
=\big[x^k\big]\big( (1-x)^i(1+x)^{n-i}\big).\]
因此
\[(-1)^{i t}D_i = [x^k]\big( (-1)^{i t}(1-x)^i(1+x)^{n-i}\big)
\]



最终得到的就是

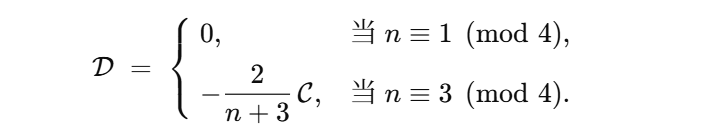
把 (2) 代回 (★):
- 若 \(n\equiv1\pmod4\),则 \(\mathcal D=0\),所以
\[ \overline m(n) = \frac{n-1}{2}.
\]
- 若 \(n\equiv3\pmod4\),则 \(\mathcal D = -\dfrac{2}{n+3}\mathcal C\),因此
\[ \overline m(n) = \frac{n-1}{2} - \frac{1}{2\mathcal C}\Big(-\frac{2}{n+3}\mathcal C\Big)
= \frac{n-1}{2} + \frac{1}{n+3}
= \frac{(n-1)(n+3)+2}{2(n+3)}
= \frac{n^2+2n-1}{2(n+3)}.
\]
做完啦。
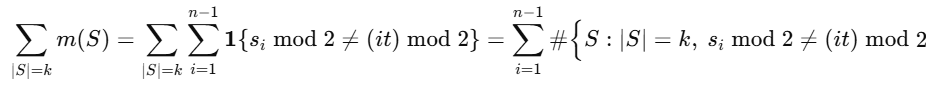



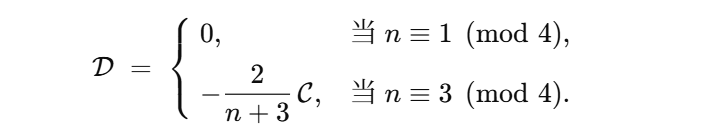





 浙公网安备 33010602011771号
浙公网安备 33010602011771号