「NOIP2018模拟9.18」最近公共祖先 - 结论题

无原题地址

最近公共祖先 (commonants.c/cpp/pas)

---

Input file: commonants.in
Output file: commonants.out
Time Limit : 0.5 seconds
Memory Limit: 512 megabytes

---

最近公共祖先（Lowest Common Ancestor,LCA）是指在一个树中同时拥有给定的两个点作为后代的最深的节点。 为了学习最近公共祖先，你得到了一个层数为 $n + 1$ 的满二叉树，其中根节点的深度为 $0$，其他 节点的深度为父节点的深度 $+1$ 。你需要求出二叉树上所有点对 $(i,j)$,（$i,j$ 可以相等，也可以 $i > j$） 的最近公共祖先的深度之和对 $1e9 + 7$ 取模后的结果。

Input

一行一个整数 \(n\) 。

Output

一行一个整数表示所有点对 \((i,j)\),（\(i,j\) 可以相等，也可以 \(i > j\)）的最近公共祖先的深度之和对 \(1e9 + 7\) 取模后的结果。

Examples

sample 1 input
2
sample 2 input
19260817
sample 1 output
22
sample 2 output
108973412

Notes

对于 \(20\)% 的数据，\(n ≤ 10\) 。
对于 \(50\)% 的数据，\(n ≤ 106\) 。
对于 \(100\)% 的数据，\(1 ≤ n ≤ 109\) 。
样例 1 解释：
树一共有 \(7\) 个节点（一个根节点和两个子节点），其中 \((4,4),(5,5),(6,6),(7,7)\) 共 \(4\) 对的最近公共祖先深度为 \(2\)，\((4,2),(2,4),(5,2),(2,5),(5,4),(4,5),(2,2),(6,3),(3,6),(3,7),(7,3),(6,7),(7,6),(3,3)\) 共 \(14\) 对最近公共祖先深度是 \(1\) ，其他的点对最近公共祖先深度为 \(0\) ，所以答案为 \(22\) 。

思路

结论题阿我整整推了一个小时阿我的青春阿阿阿阿
观察这道题，能看出是跟二叉树有关的，所以我们就能联想到二的幂数(不要问我怎么联想到的)
我一开始其实是想试图通过计算每个点对点对(断句:点 对 点对)的贡献来找规律的，结果失败了(可能因为鄙人经验欠缺吧)
于是便枚举了一下\(n\)分别等于\(1、2、3\)时对每一层的做贡献的点对个数

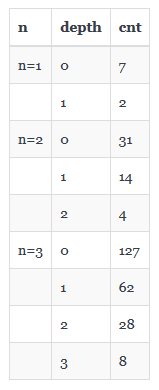
从以上表格不难得出以下式子

\(ans=\sum_{i=1}^N (2^{2n-i+1}+2^i)\times i\)

然而我推到这之后卡了半个小时=】
但是我并没有放弃 并且x绞尽脑汁想出了一个玄学的东西XD
那就是 错位相减法
接下来是推导：

\(S = 2^{2n}+2\times2^{2n-1}+3\times2^{2n-2}+...+n\times2^{n+1}-n\times2^n-...-2\times2^2-2^1\)

\(2S = 2^{2n+1}+2\times2^{2n}+3\times2^{2n-1}+...+n\times2^{n+2}-n\times2^{n+1}-(n-1)\times2^n-...-3\times2^2-2\times2^2\)

\(2S-S = 2^{2n+1}+2^{2n}+...+2^{n+2}-2^{n+1}\times2n+2^n+...+2^2+2^1\)

\(S = 2^{2n+1}+2^{2n}+...+2^{n+2}-2^{n+1}\times2n+2^n+...+2^2+2^1+1-1+2^{n+1}-2^{n+1}\)

\(S = 2^{2n+2}-1-2^{n+1}\times(2n+1)-1\)

\(S = 4^{n+1}-2^{n+1}\times(2n+1)-2\)

代码

#include<cstdio>
#include<cctype>
#define rg register
#define int long long 
using namespace std;
inline int read(){
	rg int f=0,x=0;
	rg char ch=getchar();
	while(!isdigit(ch)) f|=(ch=='-'),ch=getchar();
	while(isdigit(ch)) 	x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return f?-x:x;
}

const int mod =1e9+7;
int ans,n;
inline int power(int a,int b,int p){
	int ans=1;
	for(;b;b>>=1){
		if(b&1)	ans=ans*a%p;
		a=a*a%p;
	}
	return ans;
}
signed main(){
	freopen("commonants.in","r",stdin);
	freopen("commonants.out","w",stdout);
	n=read();
	int tmp1=power(4,n+1,mod);
	int tmp2=power(2,n+1,mod)*(2*n+1)+2;
	while(tmp1<=tmp2)	tmp1+=mod;
	ans=(tmp1-tmp2)%mod;
	printf("%lld",ans);
	return 0;
}