Solution - P3806 【模板】点分治 1
当你不知道怎么解决一道题的时候,给它凭空加一些限制条件,可能就出来了。
——不知道从哪里听来的一句话
这是点分治的一道模板题。
点分治
OI wiki 曾说过:点分治适合处理大规模的树上路径信息问题。这道题目就是一个树上路径信息问题。
点分治的基本思路是:定一个根,把路径分为三类。
- 以根节点为其中一个端点的;
- 只是经过根节点的;
- 不经过根节点的。
首先弄一棵树出来,定根为 \(1\)。(这图真大)
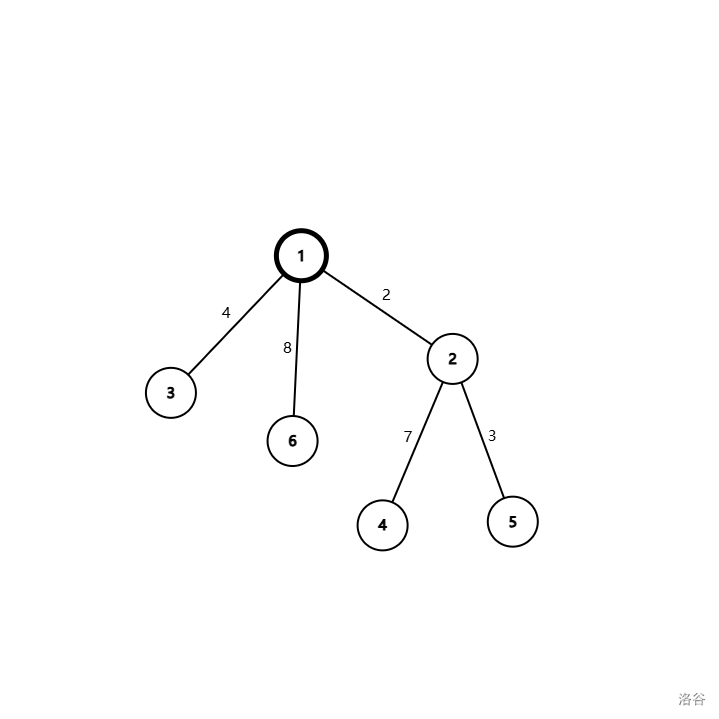
容易看出第一类和第二类都与根节点相关,于是我们先处理它们。处理方式因题而异,下面会解释,但是通常我们会把第二类路径拆成两个第一类。
假设我们已经处理完了这些路径,现在还剩第三类路径。这时,根节点已经没有存在的意义了。于是我们把它删了。图变成了这样:
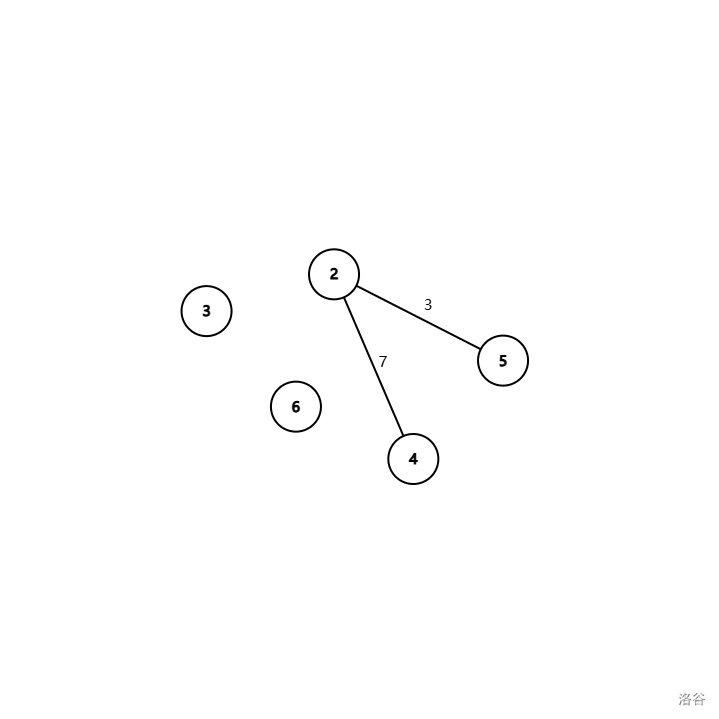
这时我们发现图变成了三颗不连通的树。然后,我们就可以贯彻分治思想,递归地处理这三棵树。于是,所有的第三类路径就都被转化成了第一类或者第二类路径。
这就是点分治的思想。
题解
以下是这道题目的题解。样例太水,给一组样例:
6 5
1 2 2
1 3 4
2 5 3
2 4 7
1 6 8
5
6
9
10
14
AYE
AYE
AYE
AYE
NAY
图例:(就是刚刚的图)

本题多测,然而给每一个询问跑一遍点分治太麻烦而且可能会被这题的神奇时限卡掉,于是离线掉询问一起处理。
于是我们给路径分类,探讨第一类和第二类路径的处理方法。
- 对于一个第一类路径(一个端点是根的路径):
我们直接对于每一个询问判断是否符合条件。在实现中为了减少码量,我们通常把它与一个根到根的长度为 \(0\) 的路径拼成一个第二类路径处理。 - 对于一个第二类路径(一个经过根的路径):
我们把它分成两个第一类路径。然后 DFS 出第一类路径,建立一个 bool 数组(或者 bitset,但是笔者不会用)存储一个距离对应的路径是否存在。然后,遍历询问,对于路径判断不在该子树内的路径中有没有长度符合(即为询问要求的长度减去当前路径的长度)的路径。若有,记录答案。
由于此后第一类路径被转化为了第二类路径,下面统称“路径”。
举个例子:
在处理以 \(1\) 为根,点集为 \(\{1, 2, 3, 4, 5, 6\}\) 的子树时,我们有路径 \(1 \to 5\) 满足询问 1 的需求,有路径 \(3 \to 2\) 满足询问 2 的需求,有路径 \(3 \to 5\) 满足询问 3 的需求,有路径 \(6 \to 2\) 满足询问 4 的需求。它们都经过了当前根 \(1\)。
对于这个过程,实现中直接对每个子树跑一遍 DFS 就行了。注意这是一个递归过程,不要跑到已经处理过的点就行了。这里切记不能偷懒对整体 DFS,否则你的算法会认为存在 \(4 \to 2 \to 1 \to 2 \to 5\) 的路径使得长度为 \(14\),满足询问 4。然而,这并不是一个路径。
然后,给当前根节点打一个标记表示已经处理,然后递归处理子树就行了。每次处理的复杂度是 \(\mathcal{O}(n)\),期望树高有 \(\mathcal{O}(\log n)\),期望复杂度 \(\mathcal{O}(n \log n)\)。
但是这就完了吗?出题人给你一个链就能把你的算法卡成 \(\mathcal{O}(n^2)\)。那怎么办?
树上有个东西叫重心,其定义为:如果在树中选择某个节点并删除,这棵树将分为若干棵子树,统计子树节点数并记录最大值。取遍树上所有节点,使此最大值取到最小的节点被称为整个树的重心。
显然就有性质:以树的重心为根时,所有子树的大小都不超过整棵树大小的一半。
于是我们每次定根的时候用 \(\mathcal{O}(n)\) 的时间求出重心,以重心为根就可以了。易证树高不大于 \(\log_2 n\)。于是复杂度就稳在了 \(\mathcal{O}(n \log_2 n)\)。
就没了。
实现
#include <bits/stdc++.h>
#define N 100005
#define VAL 10000007
using namespace std;
int to[N<<1], val[N<<1], nxt[N<<1], head[N], gsiz; // 邻接表
#define addedge(u,v,w) (++gsiz, to[gsiz]=v, val[gsiz]=w, nxt[gsiz]=head[u], head[u]=gsiz)
int vis[N], siz[N];
int exist[VAL], dis[N], cnt, tmp[N], cntt; // exist:存在性;dis, cnt:非当前子树的路径长度;tmp, cntt:当前子树的路径长度
int query[105], ans[105]; // 离线
int n, m;
inline void dfs1(int u, int fa){ // 计算子树大小,相信大家都看得懂
siz[u] = 1;
for(int i = head[u]; i; i = nxt[i]){
int v = to[i];
if(vis[v] || v == fa) continue; // 不能跑到父亲或者已经处理的节点去
dfs1(v, u);
siz[u] += siz[v];
}
return;
}
inline void dfs2(int u, int fa, int root, int& minn, int& g){ // 计算重心,想偷懒就直接用引用了
int mink = siz[root]-siz[u]; // 处理父节点方向
for(int i = head[u]; i; i = nxt[i]){ // 处理子节点方向
int v = to[i];
if(vis[v] || v == fa) continue; // 不能跑到父亲或者已经处理的节点去
mink = max(mink, siz[v]);
dfs2(v, u, root, minn, g); // 顺便就递归了
}
if(mink < minn) minn = mink, g = u; // 如果是可能的重心
return;
}
inline void dfs3(int u, int fa, int dep){
if(dep <= 1e7) tmp[++cntt] = dep; // 范围中询问小于 1e7,防止 RE
for(int i = head[u]; i; i = nxt[i]){
int v = to[i];
if(vis[v] || v == fa) continue; // 不能跑到父亲或者已经处理的节点去
dfs3(v, u, dep+val[i]);
}
return;
}
inline void solve(int u){
cnt = 0, cntt = 0; // 多测不清空,__________
dfs1(u, 0);
int minn = 1e9+7, g; // 求重心
dfs2(u, 0, u, minn, g);
vis[g] = true; // 标记一下
exist[0] = true, dis[++cnt] = 0; // 把自环加进去
for(int e = head[g]; e; e = nxt[e]){
int v = to[e]; // 对于每个子树
if(vis[v]) continue; // 已经处理的节点去
cntt = 0;
dfs3(v, g, val[e]); // 处理这颗子树的路径
for(int i = 1; i <= cntt; ++i)
for(int j = 1; j <= m; ++j)
if(query[j]-tmp[i] >= 0) // 差小于 0 时强行访问会 RE
ans[j] |= exist[query[j]-tmp[i]]; // 统计答案
for(int i = 1; i <= cntt; ++i){
dis[++cnt] = tmp[i];
if(tmp[i] <= 1e7) exist[tmp[i]] = true; // ……然后,它们就不是当前子树的路径了。
}
}
for(int i = 1; i <= cnt; ++i)
if(dis[i] <= 1e7) exist[dis[i]] = false; // 这里不能用 memset,不然复杂度就假了
for(int i = head[g]; i; i = nxt[i])
if(!vis[to[i]]) solve(to[i]); // 递归处理
return;
}
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i < n; ++i){ // 输入
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
addedge(u, v, w), addedge(v, u, w);
}
for(int i = 1; i <= m; ++i)
scanf("%d", &query[i]);
solve(1); // 处理
for(int i = 1; i <= m; ++i) // 输出
puts(ans[i] ? "AYE" : "NAY");
return 0; // CCF NOI 要求
}
实现的一些坑
- 如代码 37 行所示,需要特判路径过长的情况;
- 如代码 60 行所示,需要特判负数。
致谢
本题解参考了以下文献:
- OI Wiki - 树分治
- OI Wiki - 树的重心
- 以及诸多题解、教程与警示后人帖子,在此一并致谢。
若题解有疏漏之处,还请在评论区指出,以便拾遗补缺。另外,欢迎看一下我的 Blog,谢谢。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号