树状数组

思想由来

对于一个序列的以下两种操作：

1. 求前缀和
2. 修改某一个数

按照以往方法，具有两种解决策略：

1. 使用数组，求前缀和是\(O(n)\)的，修改一个数的是\(O(1)\)的
2. 使用前缀和数组，求前缀和是\(O(1)\)的，修改一个数是\(O(n)\)的

树状数组对两种操作的复杂度做出均衡，使得每种操作都是\(O(logn)\)的，权衡了修改和查询操作的复杂度

树状数组想要解决的核心问题是快速求区间和以及快速单点修改
核心思想为二进制拼凑

二进制拼凑的思想来源
任何一个数据\(x\)，都可以表示为以下结构
\(x = 2^{i_1} + 2^{i_2} + ··· + 2^{i_n}\)
换言之，利用\(2^{i_1}, 2^{i_2},···,2^{i_n}\)这些数据可以轻松拼凑出任意数值
那么假设我们期望求一段长度为7的区间和，那么可以考虑一种求法是依次求长度为4，2，1的子区间的区间和(顺次排列不重叠)，将其相加即为答案
4，2，1这几个长度，恰好是7的二进制展开的结果，通过二进制的形式，可以拼凑出任意长度
若将这一思想应用于区间求和，考虑将长度为x的区间\([1, x]\)划分为以下几个小区间
1.长度为\(2^{i_1}\)的子区间：\([1, 2^{i_1}]\)
2.长度为\(2^{i_2}\)的子区间：\([2^{i_1} + 1, 2^{i_1} + 2^{i_2}]\)
3.长度为\(2^{i_3}\)的子区间：\([2^{i_1} + 2^{i_2} + 1, 2^{i_1} + 2^{i_2} + 2^{i_3}]\)
...
n. 长度为\(2^{i_n}\)的子区间：\([2^{i_1} + 2^{i_2} + ··· + 2^{i_{n-1}} + 1, 2^{i_1} + 2^{i_2} + ··· + 2^{i_{n-1}} + 2^{i_n}]\)

注: 还有以下一种划分方式，可能更好理解
1.长度为\(2^{i_1}\)的子区间：\((x - 2^{i_1}, x]\)
2.长度为\(2^{i_2}\)的子区间：\((x - 2^{i_1} - 2^{i_2}, x - 2^{i_1}]\)
3.长度为\(2^{i_3}\)的子区间：\((x - 2^{i_1} - 2^{i_2} - 2^{i_3}, x - 2^{i_1} - 2^{i_2}]\)
...
n. 长度为\(2^{i_n}\)的子区间：\((0, x - 2^{i_1} - 2^{i_2} - ··· - 2^{i_{n-1}}]\)

通过\(2^{i_1}, 2^{i_2},···,2^{i_n}\)这些数据可以容易拼凑出任意一个数值，那么按照这些长度划分出的小区间也可以容易拼凑出大区间
上面的分析实际上是从最长的区间向小划分的，对于划分出的每一个子区间，还会进行细分从而划分为更小的区间，即我们是从上到下进行分析的
但是初始化应当是先求小区间，从而求解大区间，即从下到上进行初始化

对于\(x = 7\),会有如下数据
\(7 = 2^2 + 2^1 + 2^0\)
所以区间\([1, 7]\)会被划分为

1. 长度为\(4\)的区间：\([1, 4]\)
2. 长度为\(2\)的区间：\([5, 6]\)
3. 长度为\(1\)的区间：\([7, 7]\)

当然，长度为4，2，1的子区间又会进行细分

上述区间划分的结构反映到图上是一棵树形结果，因此将其命名为树状数组
理解了树状数组的原理，还需要考虑如何进行求和
观察上述区间的左右范围，可以发现，对于一个区间\([L, R]\)，满足\(R - L + 1 = lowbit(R)\)
例如长度为\(2^{i_2}\)的子区间\([2^{i_1} + 1, 2^{i_1} + 2^{i_2}]\)，\((2^{i_1} + 2^{i_2}) - (2^{i_1} + 1) + 1 = 2^{i_2}\)
而\(2^{i_2}\)恰为\(lowbit(2^{i_1} + 2^{i_2})\)
换言之，当我们知道区间右端点时，我们就可以算出区间长度，从而得知区间左端点，即\(L = R- lowbit(R) + 1\)

当我们希望求解\([1, 5]\)的区间和时，我们需要知道这段区间是如何进行划分的
按照上述讨论的性质，根据右端点\(5\)，我们可以确定右端点为\(5\)的一个子区间为\([5 - lowbit(5) + 1, 5]\), 即\([5, 5]\)
从而更靠前的子区间右端点为\(4\)，再次根据上述性质，计算得出右端点为\(4\)的一个子区间为\([1, 4]\)
假设我们预处理了以R为右端点，区间长度为lowbit(R)的区间的和，记为\(c[R]\)
则\([1, 5]\)的区间和等于c[5] + c[4]
不难，发现，上述的求解过程，等价于以下代码

inline int lowbit(int x) {
    return x & -x;
}
int ask(int x) {
    int ans = 0;
    for (; x; x -= lowbit(x)) ans += c[x];
    return ans;
}

上述过程根据区间的划分方法分析出一种根据区间右端点确定区间的方法，利用这种方法，我们可以快速求出区间和

因为我们将区间长度依次划分为\(2^{i_1}, 2^{i_2},···,2^{i_n}\),对于7，有\(7 = 2^2 + 2^1 + 2^0\)
\(lowbit(7) = 2^0, 7 - lowbit(7) = 2^2 + 2^1 = 6\)
\(lowbit(6) = 2^1, 6 - lowbit(6) = 2^2 = 4\)
\(lowbit(4) = 2^2, 4 - lowbit(4) = 0\)
而7，6，4恰好指代的就是那几段子区间，所以这也就解释了为什么在上述代码中，ans加上的c[x]的x始终在减去自己的lowbit(x)

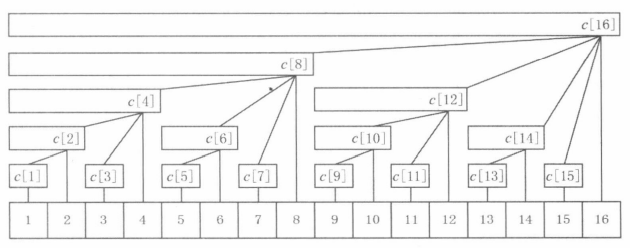
c[x]的父节点是cx + lowbit(x)
所以在向a[x]添加y时的代码为

inline int lowbit(int x) {
    return x & -x;
}
void add(int x, int y) {
    for (; x < N; x += lowbit(x)) c[x] += y;
}

初始化c数组的方式可以考虑a数组初始为全0，直接采用add(x, a[x])

树状数组本质只是一种工具，当我们面对需要进行修改操作的区间和查询问题时，可以采用这种工具
所以问题的核心在于对于一道题目分析出，其需要区间和查询和单点修改操作，然后采用树状数组解决即可

问题描述

序列：5 6 3 2 4 1 9
对于序列a中某个位置的数值v，期望快速求出在此之前出现过的比v小的数的个数
5： 此前没有出现过比5小的数，答案为0
6： 5<6，答案为1
3： 答案为0
2： 答案为0
4： 3,2<4, 答案为2
1： 答案为0
9： 此前数据全部小于9，答案为6

对于这样一个问题，假设我们维护的c[R]表示数值处在1到R中的元素个数
对于上述给定例子，对于每次遍历到的数值v，答案就等于c[v-1]

但是考虑在常规前缀和的实现方式中我们应当如何维护这样一个c数组
c[R]表示处在1到R中的元素个数，假设此时添加一个新元素为5，且最大范围到10，那么需要更新的是c[5], c[6], c[7], c[8], c[9], c[10]
按照c的定义，在更新时需要更新多个，而非仅c[5]一个元素
这样预处理的方式是\(O(n^2)\)的，大部分数据范围都无法接受

这里涉及到的就是求区间和，以及单点修改(从这里可以看出，单点修改不是常规前缀和的问题，瓶颈是单点修改后区间和的更新问题)，
所以可以考虑使用树状数组，将操作优化为\(O(nlogn)\)