本周任务：
请确保熟悉并理解机器学习数学部分常用相关概念:
1.高等数学
1）函数
2）极限
3）导数
4）极值和最值
5）泰勒级数
6）梯度
7）梯度下降
2.线性代数
1）基本概念
2）行列式
3）矩阵
4）最小二乘法
5）向量的线性相关性
3.概率论
1）事件
2）排列组合
3）概率
4）贝叶斯定理
5）概率分布
6）期望和方差
7）参数估计
答：
本福特定律：
概率公式：
贝叶斯公式：
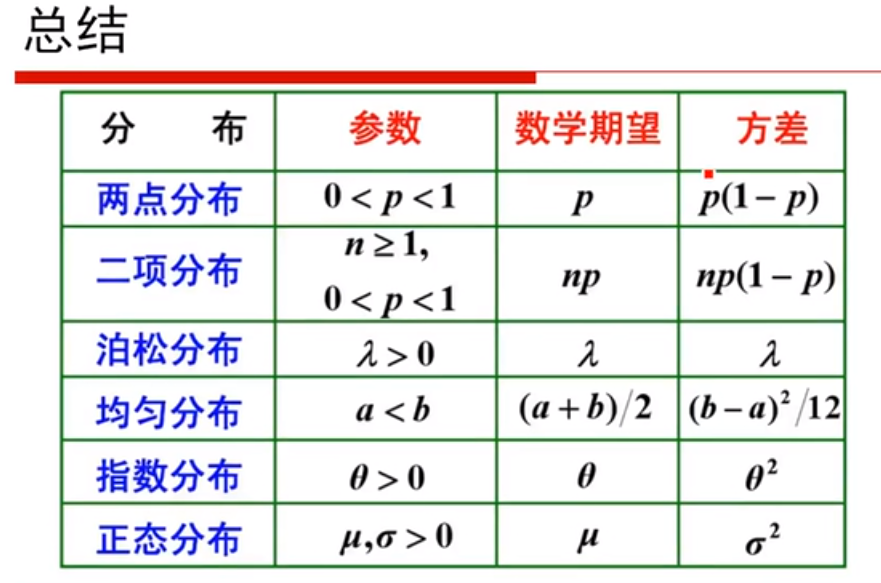
两点分布：
二项分布：
Taylor展式：
泊松分布
均匀分布
指数分布
指数分布的无记忆性
正态分布
beta分布
sigmoid函数导数
事件的独立性
期望的性质
方差
协方差和独立、不相关
pearson相关系数
伯努利定理
中心极限定理
矩阵学习主要内容
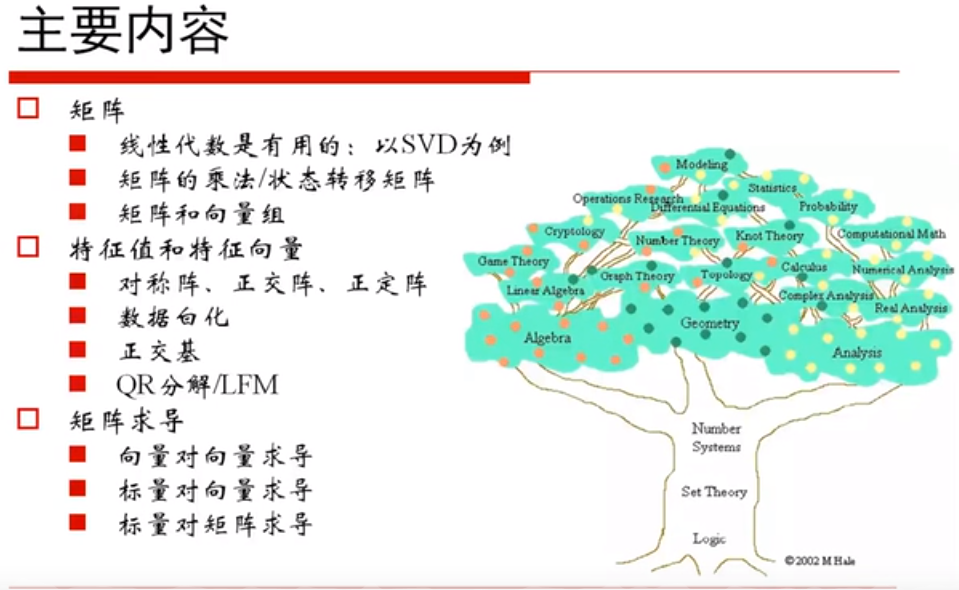
线性代数
范德蒙行列式
矩阵和向量乘法
矩阵的秩
正交阵
2.本周视频学习内容：https://www.bilibili.com/video/BV1Tb411H7uC?p=2
1）P2 概率论与贝叶斯先验
2）P3 矩阵和线性代数
机器学习是一门多领域交叉学科，涉及较多的数学知识，本节课知识之前都有学过，这次根据重点重新梳理一遍，一定要多加重视。通过观看视频，大家对课程的数学基础部分加深印象。
建议大家边看边做笔记，记录要点及所在时间点，以便有必要的时候回看。学习笔记也是作业的一部分。
答：
总结
梯度：从几何意义上讲，就是函数变化增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。
梯度下降：机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。
贝叶斯定理：通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系,贝叶斯定理就是这种关系的陈述。
3.作业要求：
1）贴上视频学习笔记，要求真实，不要抄袭，可以手写拍照。
2）用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”，可以word编辑，可做思维导图，可以手写拍照，要求言简意赅、排版整洁。
