云心出岫——Splay Tree
(多图预警!!!建议在WiFi下观看)
之前我们谈论过AVL树,这是一种典型适度平衡的二叉搜索树,成立条件是保持平衡因子在[-1,1]的范围内,这个条件已经是针对理想平衡做出的一个妥协了,但依然显得过于苛刻,因为在很多时候我们需要频繁的做重平衡操作,能不能改进一下,让失衡先积累着,然后等到某个时机,一下子全部解决呢?严谨一点来说就是我们能否秉持一种更为宽松的准则,同时又从长远、整体的角度来看,依然不失某种意义上的平衡性呢?如果比作人的话,AVL树就犹如那种处处谨慎的性格,一点风吹草动就要调整自己。那么……能否成为那类更为潇洒的人呢?怎样才能御风蓬叶,泛彼无垠,不被苛刻的平衡所拘束呢?
根据写作套路,那肯定就是点题了……对!就是伸展树了,他的出现是因为有人注意到了在信息处理过程中的“局部性”,就是刚被访问过的数据,极有可能很快的被再次访问到,只要针对这个特性大做文章,就能切中肯綮,而不用对“保持平衡”这件事风声鹤唳了。这也是下面我们要分析的重点。
在二叉搜索树里也时常遇到,主要是两种情况:
- 每次刚刚访问过的某一个节点有可能很快的会再次被我们访问到
- 下次访问的节点即便不是刚访问过的那个节点,也不会离得太远
通过此前的学习我们已经知道,对于AVL树而 每一次查找所需的时间都是logn,因此任意的连续m次查找,所需要的累积时间就是mlogn,为了改进,就针对这个局部性来做一做文章吧:
先来看一个例子,然后类比推理即可。链表里越靠近表头的节点的查找速度越快,遍历所走的步数少嘛,那么如果数据访问有局部性,我们就——访问一个元素后立即把他移动到最前端。

这样做的逻辑是:根据局部性,接下来将要访问的元素很可能就是刚访问的那个元素,而这个元素就在最前端,头部元素的访问是访问是唾手可得的,走一步就到了。从整个数据结构的生命周期而言,这样一个列表结构即便最初是完全随机分布的,在经过了足够长时间的使用之后,在某一段时间内被集中访问的元素都会集中到这个列表的前端去。我们已经知道这个区域(列表前段部分)的访问效率是相应更高的,那就能有更高的访问效率了。
现在回到二叉树,为了对比就让树横过来。
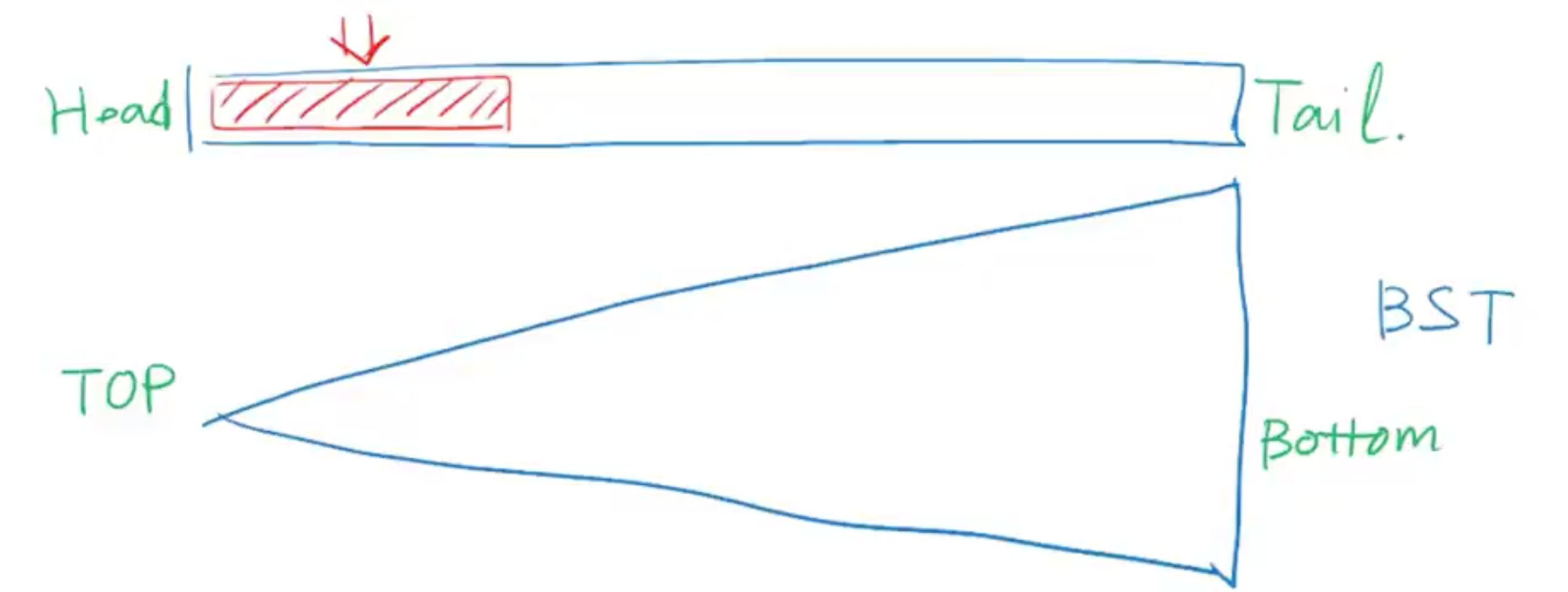
树的顶部元素访问效率更高,所以我们要参照列表,把经常要访问到的元素尽可能的移送到接近树根的位置,也就是要尽可能的降低他们的深度。

那我们就这么办:某个元素一经访问,就把它移到树根处。具体做法就是把被访问元素不断做旋转操作直到抵达树根,这样的策略被称为“逐层伸展”,是一种朴素的想法,但是不够好,因为在最坏情况下树退化为一条单链,我们来个极端的,每次恶意访问最深的节点,就会变成这样:

先注意一下特征:每层只挂了一个节点,这是弊端所在,后面还会提到。然后经过一轮询问,这个树就复原了。看一下整个过程(竖着看)
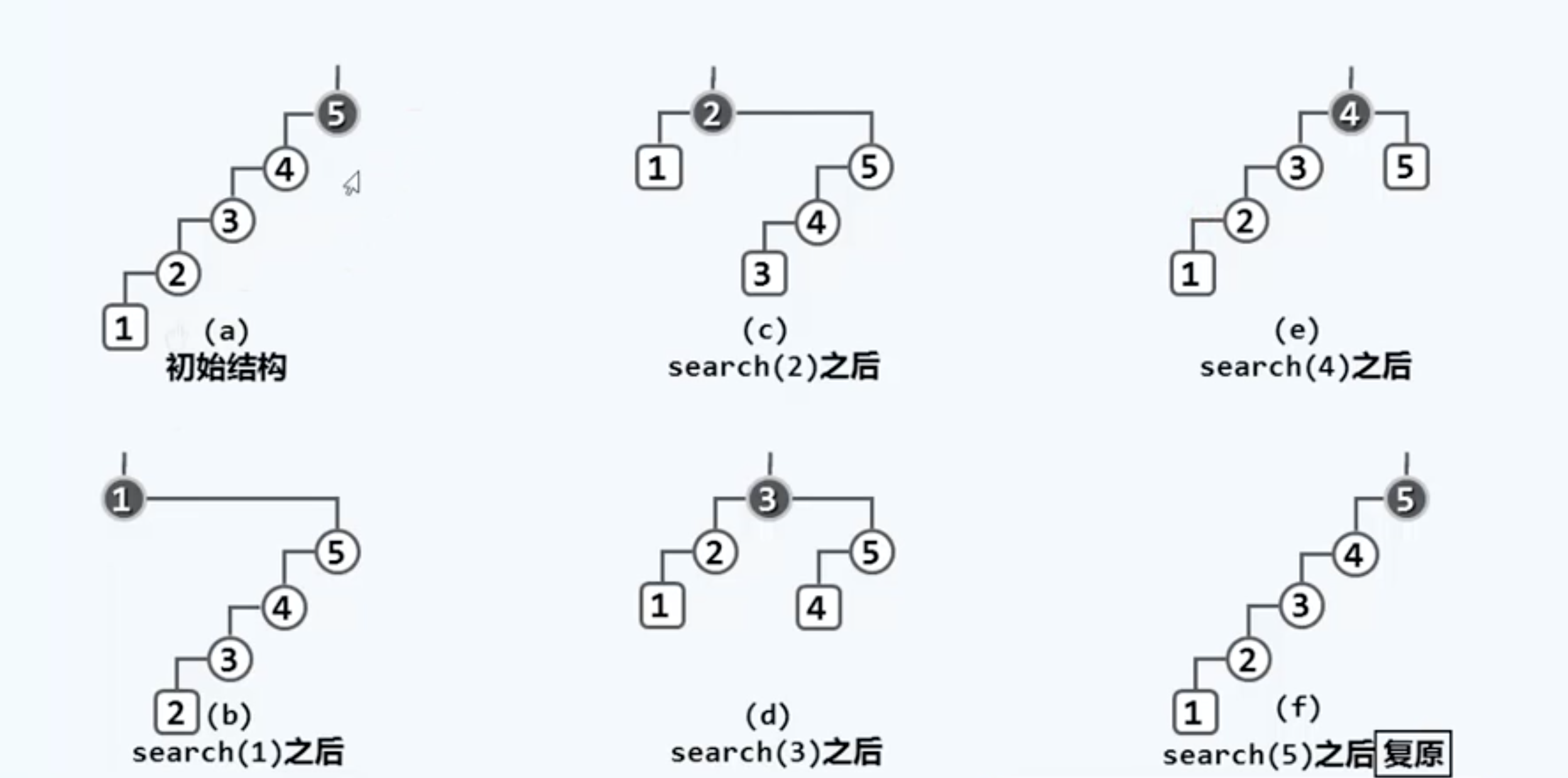
我们分析一下这一轮操作的代价:假设树的规模是n,访问第一个最深节点的成本是n,第二个节点是n-1,第三个是n-2,然后是n-3,n-4和最终的1。整个成本按算术级数增长,这就很恐怖了,总体时间O(N2),分摊到整个周期的n次操作,复杂度Ω(N)居高不下,和AVL树的logN相差甚远,这已经沦落到了线性序列的地步。另外还有一个弊端在于:我们需要为此考虑很多种特殊情况。所以这个策略无法让人满意。
我们还要另找方法——在初始访问路径上进行一些神奇的旋转,只用了O(1)的空间,而且保持O(logN)的时间复杂度。
具体而言就是:双层伸展,向上追溯两层,通过两次旋转把被访问节点上移至祖父的位置,而且!不是像之前一样自下而上伸展,而是自顶向下进行伸展。这可以说是SplayTree的点睛之笔。这是在1985年Tarjan大神的一篇论文《Self-adjusting binary search trees》里提出来的,有兴趣可以去Google Scholar上瞻仰一番(和他有关的还有一个Tarjan算法,是关于图的连通性的神奇算法)。祖孙三代的相对位置无非四种:

子孙异侧
先从难啃的骨头开始。有些书上会把这种情况称为“之字形”,以此为例:
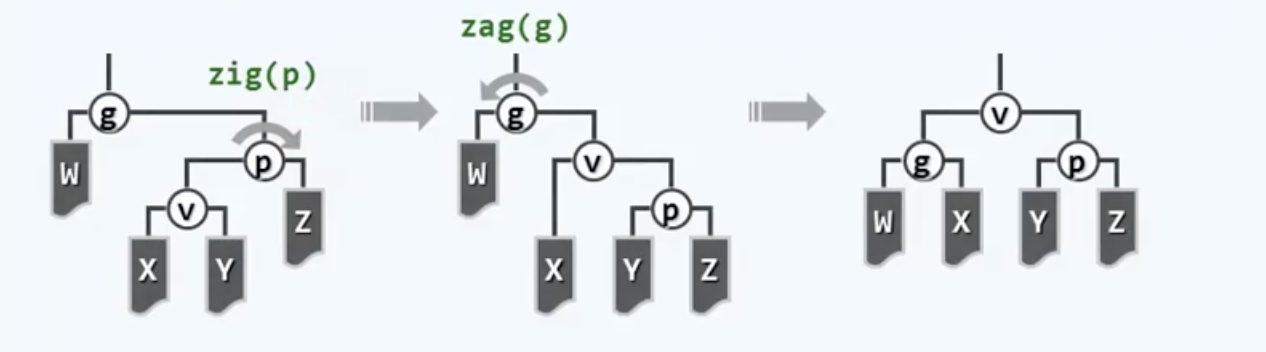
“这特么不就是双旋转么,而且这也就是逐层伸展两次而已,没什么实质区别啊(摔)”,没错,这个部分区别不大,但重点在于另外这条龙一只眼睛,那才是闪光之处:
子孙同侧
有些书上也称为“一字形”。我们先看一下逐层伸展的调整过程,然后和Tarjan的策略作一比较,就知道差距有多大了。

这是我们凡人想到的方法。下面是Tarjan的点睛之笔:

这里的重中之重是:需要首先越级,从祖父而不是父节点来开始旋转,具体来说就是,经过祖父节点的一次左-左旋转,节点p以及v都会上升一层。接下来对新的树根也就是p,再做一次左-左旋转,把v拉上来成为树根,Done。把这两种方法作一对比,emmm好像没什么大差别啊,是吧?的确这里面的神奇之处一时半会难以察觉,看起来反正都是提高了两层倍,不过它们在局部拓扑结构上还是有微妙差异的,更重要的是——这种局部的微妙差异将导致全局的不同,而且那种不同将是根本性的、颠覆性的!Splay Tree在这个伸展方式的革命中失去的只是锁链,他们获得的将是整个世界。
现在来看看这个差异所带来的利好。如果用这种方式我们再来访问最深的节点,会有什么改进呢?
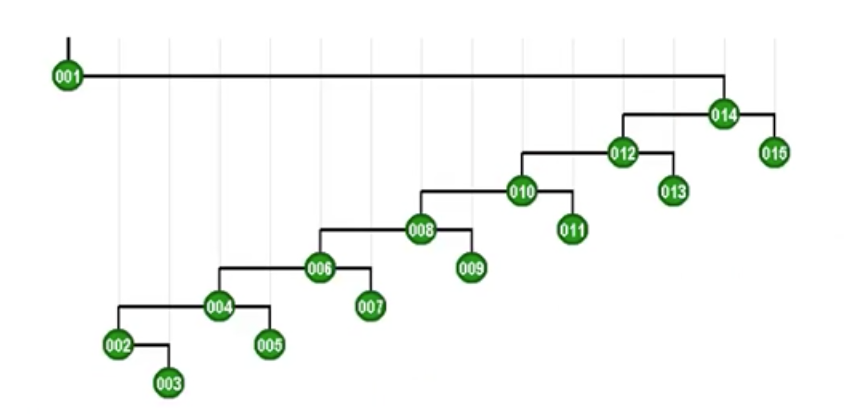
现在的改进在于每一层能挂更多的节点了,这就是有效控制树高的一个方法。之前说的逐层伸展最坏情况之所以“坏”是因为,尽管能调整到树根,但是在这个过程中树的高度会以算术级数的速度急剧膨胀,这是一种不计后果的方法,所以很坏。而Tarjan的方法优越性在于,在每次即使访问最深的节点时候,也能控制树高,渐进意义上是之前逐层伸展树高的一半,记得前面说的“会导致全局的不同”么,就是这里的树高缩减一半!这个特性太好了,节点越多,访问次数越多,这个控制的效果越明显,这也被称为SplayTree的折叠效果。那么总结一下双层伸展的核心优势——

通过这个例子可以看出:任何一个节点经过访问,再经双层调整后,这个节点所在的路径长度就会减半。甚至可以说——这种效果具有某种意义上的智能:既然在一棵BST中非常忌讳访问很深的节点(这会导致复杂度急剧上升),那这种折叠效果自然就会具有对坏节点的修复作用,我们就不必担心了。犹如含羞草一旦感受到威胁,就会通过迅速收缩,将自己的弱点隐藏起来。因此在采用Tarjan所建议的这种新的策略之后,刚才所举的那种最坏情况就不至持续的发生,可以证明的是单次操作的时间上界是O(logN)。这也就是说!我们现在不仅足以应对此前涉及的最坏情况,而且也不会有任何其他的最坏情况,这是一个再好不过的消息了,简直让人开心到爆炸啊!
复习一下:对Splay Tree最合适的做法是双层伸展,即向上追溯两层,通过两次旋转把被访问节点上移至祖父的位置,并且宏观看来是自顶向下进行伸展。
现在我们先把以上的伸展策略由理想变为现实,然后以此作为基础,去缔造更丰富的功能。
先给出相关的类型声明和要用到的组件:
1 #ifndef Splay_h 2 #define Splay_h 3 struct SplayNode; 4 typedef struct SplayNode *SplayTree; 5 typedef struct SplayNode *Position; 6 SplayTree FindIn(int x,SplayTree T); 7 SplayTree Splaying(int Item,Position X); 8 SplayTree Insert(int Item,SplayTree T); 9 SplayTree Remove(int Item,SplayTree T); 10 SplayTree FindMin(SplayTree T); 11 Position FindMax(SplayTree T); 12 int Retrieve(SplayTree T); 13 #endif /* Splay_h */ 14 15 16 struct SplayNode{ 17 int value; 18 SplayTree left; 19 SplayTree right; 20 }; 21 22 static Position SingleRotateWithLeft(Position p){//zig 23 Position temp=p->left; 24 p->left=temp->right; 25 temp->right=p; 26 return temp; 27 28 }//zig 29 30 31 static Position SingleRotateWithRight(Position g){ 32 Position temp=g->right; 33 g->right=temp->left; 34 temp->left=g; 35 return temp; 36 }//zag
然后我们要把一棵树从无到有的过程给做出来
1 static Position Origin=NULL; 2 3 SplayTree Init(){ 4 if (!Origin) { //When the tree we talked about is non-exsitent. 5 Origin=(SplayTree)malloc(sizeof(struct SplayNode)); 6 Origin->left=Origin->right=NULL; 7 } 8 return Origin; 9 }
这里用Origin代表空指针是为了代码的可读性,这样日后再看起来就能通过变量名清晰地理解代码含义了。不至于过三个月自己写的代码都看不懂2333
下面给出双层伸展过程,这是一个被动技能,上一篇里讲的已经很清楚了所以注释就稍微简略一些。
1 //Top-down splay procedure,not requiring Item to be in the tree 2 SplayTree Splaying(int Item,Position X) { 3 static struct SplayNode Header; 4 Position LeftMax,RightMin; 5 6 Header.left=Header.right=Origin; 7 LeftMax=RightMin=&Header; 8 Origin->value=Item; 9 10 while (Item != X->value) { 11 if (Item < X->value) { 12 if (Item < X->left->value) { 13 X=SingleRotateWithLeft(X); 14 } 15 if(X->left==Origin) 16 break; 17 //Link right 18 RightMin->left=X; 19 RightMin=X; 20 X=X->left; 21 } 22 else{ 23 if(Item > X->right->value) 24 X=SingleRotateWithRight(X); 25 if(X->right==Origin) 26 break; 27 //Link left 28 LeftMax->right=X; 29 LeftMax=X; 30 X=X->right; 31 } 32 }//while Item != X->value 33 34 //Reassemble 35 LeftMax->right=X->left; 36 RightMin->left=X->right; 37 X->left=Header.right; 38 X->right=Header.left; 39 40 return X; 41 }
然后是插入,这个要分情况讨论。假设T是当前的树根,如果T是空树,那么我们建立一颗单节点树。否则的话就围绕着Item把T展开,先把T提到树根的位置(下面的两种情况演示都建立在执行过对T伸展之后)。如果已经存在这个元素,就什么也不做,直接返回。其他的情况就剩ins > T 或者 ins < T 了,我们来分别讨论,比如在下图中插入5
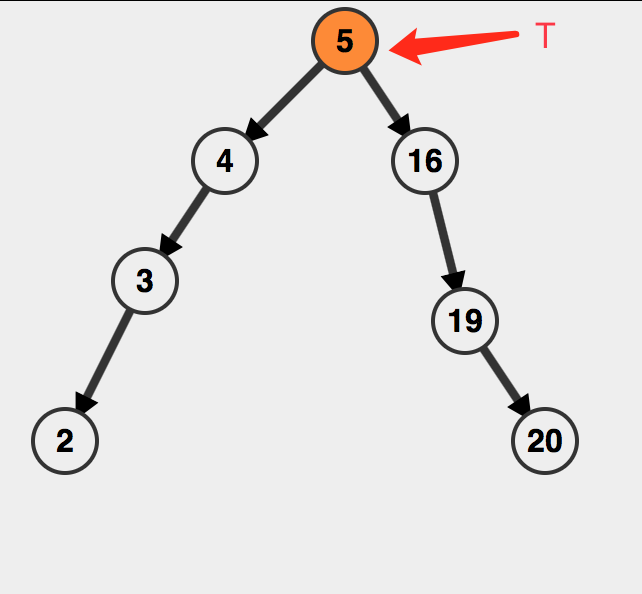
第一步先申请一个节点

然后比较当前根和待插入节点的数值,如果根大了的话,那么就让T和它的右子树一同作为newNode的一棵右子树,相应地让T的左子树成为newNode的左子树。并且让T的左指针收回去。

最后因为要返回T,把T所存的地址变更为新的树根即可。
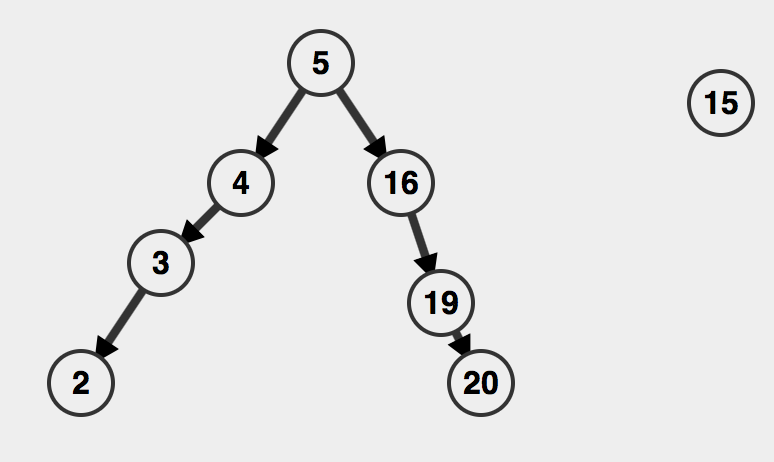
一道非常美味的Splay树插入过程就制作完成了。
这是根>待插入节点,那如果根<待插入节点呢?逻辑是类似而又对称的。比如在上图的基础上插入15
比较root的值和ins的值,比root大,那就让T和它的左子树一同作为newNode的左子树,让T的右子树成为newNode的右子树。

最后变更一下T的值,即可。
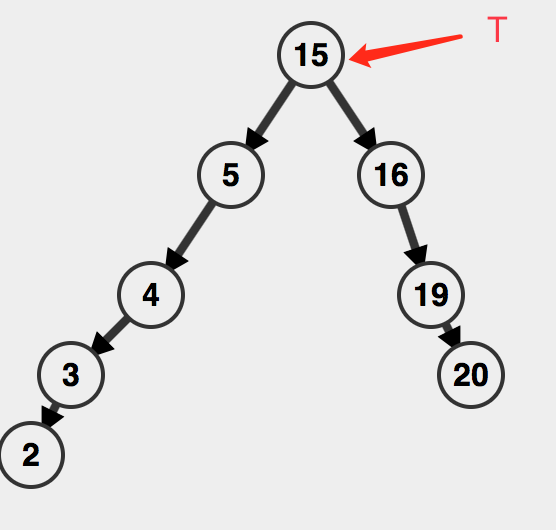
其他的细节都很好理解了:
1 SplayTree Insert(int Item,SplayTree T) { 2 //T means original root 3 static Position NewNode=NULL; 4 if (!NewNode) 5 { 6 NewNode=malloc(sizeof(struct SplayNode)); 7 } 8 NewNode->value=Item; 9 10 if (T==Origin) 11 { 12 NewNode->left=NewNode->right=NULL; 13 T=NewNode; 14 } 15 else 16 { 17 T=Splaying(Item, T); 18 if (T->value > Item) 19 { 20 //look at left subtree 21 NewNode->left=T->left; 22 NewNode->right=T; 23 T->left=Origin; 24 T=NewNode; //make inserted element as root of tree 25 } 26 else if(T->value < Item) 27 { 28 //look at right subtree 29 NewNode->right=T->right; 30 NewNode->left=T; 31 T->right=Origin; 32 T=NewNode; //make inserted element as root of tree 33 } 34 else return T; //Already in the tree,we do nothing. 35 36 } 37 38 NewNode=NULL; 39 // it given convince for the next insert,then next insert will call malloc straightly 40 41 return T; //always make the parameter T act as the root be returned 42 43 }
最后说删除,这个删除就轻松多了,因为每次展开之后,待删除的元素已经放在根的位置了。话说删除过程比对应的插入过程还要简短,这实属罕见.....
先举个例子,我们要删除5。这是删除前的图,用T表示删除之前全树的树根(切记,不然后面容易搞混):
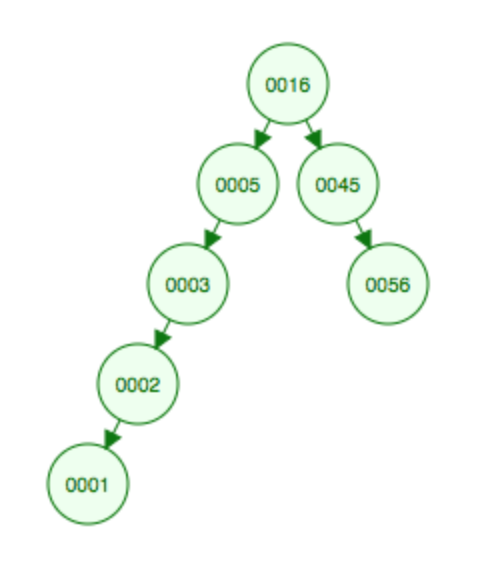
对5做一次Splaying,就到顶点了。
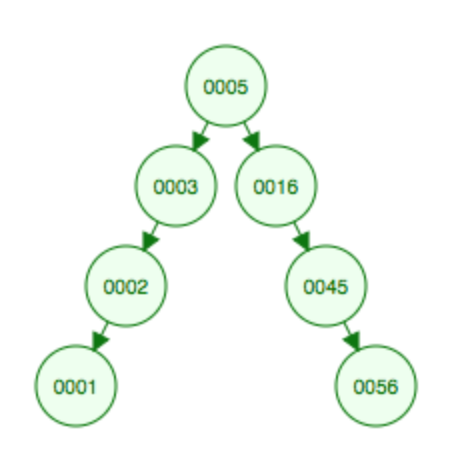
当根左子树存在的时候,临时节点(new tree)抓住left subtree,以便作为日后的根,接着做一次展开,Newtree就变成新的根了,然后让newTree的右侧挂钩抓住T的右子树…我自己画个图吧

然后把原来的根T(所指的那块内存)free掉,当然这时候T还是存在的,只是那块内存还给OS了。

接下来为了保持程序逻辑的统一性,我们还是返回T,为了让T指向正确的位置,就让T指向当前的根。

大功告成,然后把T打发回去就好了。具体过程如下:
1 SplayTree Remove(int Item,SplayTree T){ 2 Position NewTree; // 3 if (T) { 4 T=Splaying(Item, T); 5 if (Item==T->value) { 6 //primarily we find it 7 if(!T->left) 8 NewTree=T->right; 9 else{ 10 NewTree=T->left; 11 NewTree=Splaying(Item, NewTree); 12 NewTree->right=T->right; 13 } 14 free(T); 15 T=NewTree; 16 } 17 } 18 19 return T; 20 }
写到这里我不禁想吐槽一下课本,多给点步骤图不行么……我一开始脑内调试了好久才完全理解的。为了减轻我们的学习成本,我就把里面每一个步骤的分解动作都画出来了,希望能弥补原书缺少实例的这一缺憾吧,书是好书,就是太抽象了2333 如果光看代码没有实例步骤图,只有抽象的开始图片和结束图片,就很难迅速理解。
伸展树到这里就结束了,下一站是——B-树!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号