均匀性度量图像分割算法分析

均匀性度量图像分割是图像像素分割的一种方法，当然还有其他很多的方法。这里简单的介绍下其原理和实现代码【有源码】

其流程大概分为一下几步

1、确定一个阈值
2、计算阈值两边的像素个数、占比、以及方差
3、将两边的方差和占比想乘再相加
4、循环1~3的步骤
下面以这个例子为示例做一个演示

计算公式：

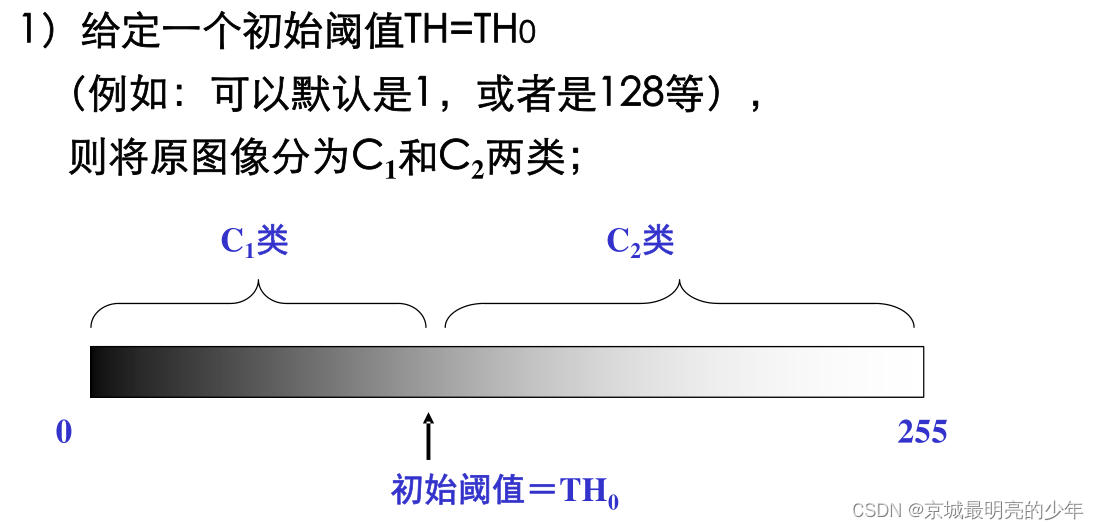
阈值为: 1
阈值左边值为: [1, 1, 0, 0, 0] 均值: 0.08
阈值右边值为: [3, 9, 9, 8, 2, 3, 7, 3, 3, 6, 6, 4, 6, 8, 2, 5, 2, 9, 2, 6] 均值: 4.12
阈值左边方差为: 1.712
阈值右边方差为: 147.76800000000003
方差和比例相乘为: 118.55680000000002

阈值为: 2
阈值左边值为: [1, 2, 1, 0, 2, 0, 2, 2, 0] 均值: 0.4
阈值右边值为: [3, 9, 9, 8, 3, 7, 3, 3, 6, 6, 4, 6, 8, 5, 9, 6] 均值: 3.8000000000000007
阈值左边方差为: 11.440000000000003
阈值右边方差为: 150.04
方差和比例相乘为: 100.144

阈值为: 3
阈值左边值为: [1, 3, 2, 1, 3, 3, 3, 0, 2, 0, 2, 2, 0] 均值: 0.8799999999999999
阈值右边值为: [9, 9, 8, 7, 6, 6, 4, 6, 8, 5, 9, 6] 均值: 3.3200000000000003
阈值左边方差为: 25.347200000000004
阈值右边方差为: 186.14879999999997
方差和比例相乘为: 102.53196799999999

阈值为: 4
阈值左边值为: [1, 3, 2, 1, 3, 3, 3, 0, 4, 2, 0, 2, 2, 0] 均值: 1.0399999999999998
阈值右边值为: [9, 9, 8, 7, 6, 6, 6, 8, 5, 9, 6] 均值: 3.16
阈值左边方差为: 31.0624
阈值右边方差为: 199.56159999999997
方差和比例相乘为: 105.20204799999998

阈值为: 5
阈值左边值为: [1, 3, 2, 1, 3, 3, 3, 0, 4, 2, 0, 5, 2, 2, 0] 均值: 1.2399999999999998
阈值右边值为: [9, 9, 8, 7, 6, 6, 6, 8, 9, 6] 均值: 2.96
阈值左边方差为: 41.18400000000001
阈值右边方差为: 213.536
方差和比例相乘为: 110.12480000000001

阈值为: 6
阈值左边值为: [1, 3, 2, 1, 3, 3, 3, 6, 0, 6, 4, 6, 2, 0, 5, 2, 2, 6, 0] 均值: 2.1999999999999997
阈值右边值为: [9, 9, 8, 7, 8, 9] 均值: 2.0
阈值左边方差为: 88.96000000000002
阈值右边方差为: 244.0
方差和比例相乘为: 126.16960000000002

阈值为: 7
阈值左边值为: [1, 3, 2, 1, 3, 7, 3, 3, 6, 0, 6, 4, 6, 2, 0, 5, 2, 2, 6, 0] 均值: 2.4800000000000004
阈值右边值为: [9, 9, 8, 8, 9] 均值: 1.7200000000000002
阈值左边方差为: 103.488
阈值右边方差为: 237.87199999999996
方差和比例相乘为: 130.3648

阈值为: 8
阈值左边值为: [1, 3, 8, 2, 1, 3, 7, 3, 3, 6, 0, 6, 4, 6, 8, 2, 0, 5, 2, 2, 6, 0] 均值: 3.12
阈值右边值为: [9, 9, 9] 均值: 1.08
阈值左边方差为: 143.4368
阈值右边方差为: 188.17919999999998
方差和比例相乘为: 148.805888

---

2
100.144

结论：

最后我们发现 以像素点为4的来分的时候，两边方差与占比的乘积最小，因此最佳阈值就是 【2】

源码

import numpy as np
#
data = [1, 3, 9, 9, 8,
        2, 1, 3, 7, 3,
        3, 6, 0, 6, 4,
        6, 8, 2, 0, 5,
        2, 9, 2, 6, 0]
# data = [0, 1, 3, 1, 5,
#         7, 8, 9, 7]
max = np.max(data)


length = len(data)

num_min_data = []
num_max_data = []
arr_var = 0
min_result = 1000
result_threshold = 0

def myMean(arrs):
        resultss = 0.0
        data={}
        for i in arrs:
                data[i]= data.get(i,0)+1
        for i in data:
                resultss += i*(data[i]/length)
        return resultss
def fz(arrs):
        results = 0.0
        mean = myMean(arrs)
        for i in arrs:
                results+=(mean-i)**2
        return results

for i in range(1,max):
        num_min_data = []
        num_max_data = []
        for j in range(length):
                if data[j]>i:
                        num_max_data.append(data[j])
                else:
                        num_min_data.append(data[j])
        arr_var_max = fz(num_max_data)
        arr_var_min = fz(num_min_data)
        print("----------------------------------")
        print("阈值为:",i)
        print("阈值左边值为:",num_min_data,"均值:",myMean(num_min_data))
        print("阈值右边值为:",num_max_data,"  均值:",myMean(num_max_data))
        print("阈值左边方差为: ",arr_var_min)
        print("阈值右边方差为: ",arr_var_max)
        ratio_left   = arr_var_min*len(num_min_data) / length
        ratio_right  = arr_var_max*len(num_max_data) / length
        ratio_last = ratio_left+ratio_right
        print("方差和比例相乘为: ",ratio_last)
        if (ratio_last<min_result):
                min_result = ratio_last
                result_threshold = i

print("*"*50)
print(result_threshold)
print(min_result)