2022春每日一题：Day 39

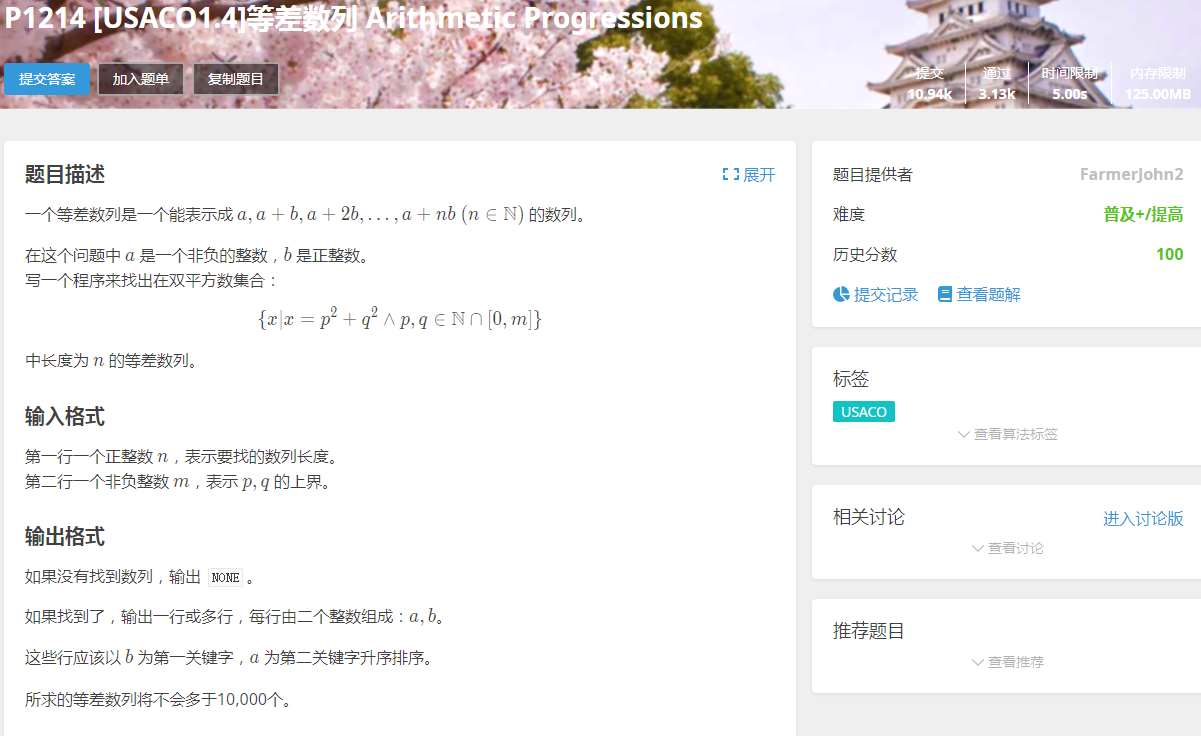
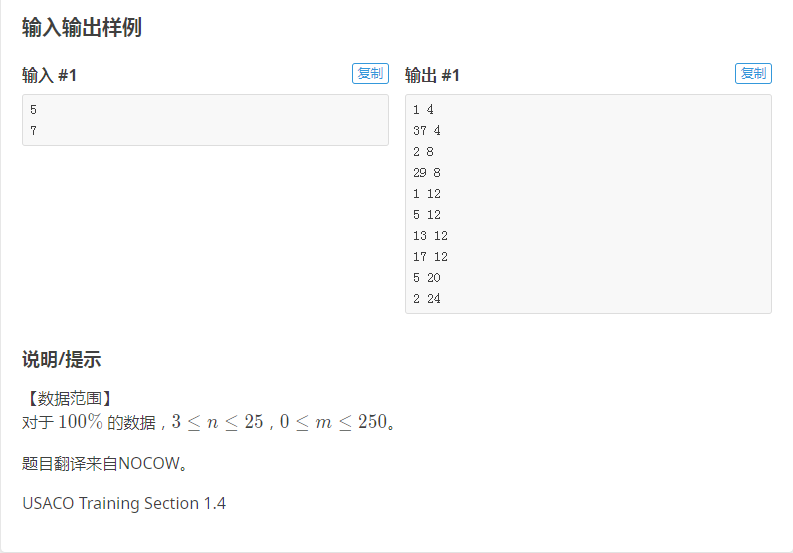
题目：[USACO1.4]等差数列 Arithmetic Progressions

一个很显然的做法，枚举公差，首项，p,q这样的话复杂度爆炸，不过可以肯定的一点，如果我们这样做，找到了答案就可以直接输出

考虑优化，m很小，可以打表把p^2+q2所有可能的答案用桶存下来，枚举之用一个数，另一个数直接通过数学计算得出，在中途无解时，直接跳出，剪枝。
这样的话已经可以通过本题，但是考虑继续优化，不难发现n>=4时，公差一定是4的倍数，因为我们知道i与i+1是互质的，而n=3时，0,1,2是允许的，而且2^2是4，所以公差至少为4。
这样每个点都可以跑进1s内

代码：

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
const int N=250*255*2;
using namespace std;
int n,m,maxs,ret,t[N],s[N],cnt;
int main()
{
	scanf("%d %d",&n,&m);
	maxs=m*m+m*m;
	for(int i=0;i<=m;i++)
	    for(int j=0;j<=m;j++)
	        t[i*i+j*j]=1;
	for(int d=1;d<=maxs;)
	{
		for(int f=0;f+(n-1)*d<=maxs;f++)
		{
			int cnt=0;
			for(int i=1;i<=n;i++)
			{
				int flag=1;
				if(!t[f+(i-1)*d])
				    flag=0;
				cnt+=flag;
				if(cnt!=i)
				    break;
			}
			if(cnt==n)
			    printf("%d %d\n",f,d),ret++;
		}
		if((n-1)*d>maxs)
		    break;
		if(n==3)
		    d++;
		else
		{
		    d+=4;
		    if(d==5)
		        d--;
		}
	}
	if(!ret)
	    puts("NONE");
	return 0;
}