论文查重

目录

• 作业要求
• PSP表格
• 程序设计及结构
• 算法分析
• 测试数据

一、作业要求

这个作业属于哪个课程	软件工程
这个作业要求在哪里	软件工程作业要求
这个作业的目的	使用PSP表格估计程序开发所需时间，使用gitcode管理代码，学会自动测试程序并返回测试结果
GitCode链接	我的GitCode仓库

二、PSP表格

PSP2.1	personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	20	30
Estimate	估计这个任务需要多少时间	90	80
Development	开发	900	1020
Analysis	需求分析	80	120
Design Spec	生成设计文档	60	50
Coding Standard	代码规范	30	40
Design	具体设计	130	120
Coding	具体编码	400	520
Code Review	代码复审	30	50
Test	测试	50	80
Reporting	报告	150	130
Size Measurement	计算工作量	30	25
Postmortem & Process Improvement Plan	事后总结并提出过程改进计划	60	60
All	总计	2030	2325

三、程序设计及结构

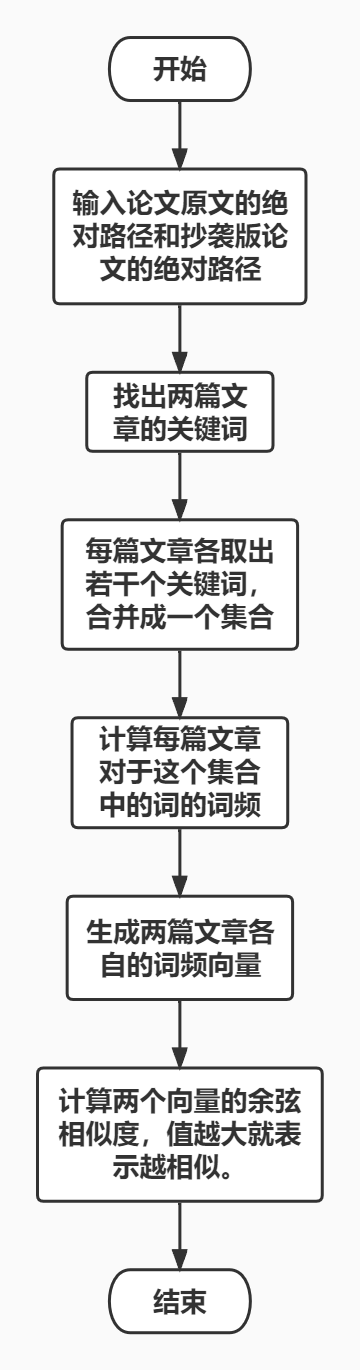
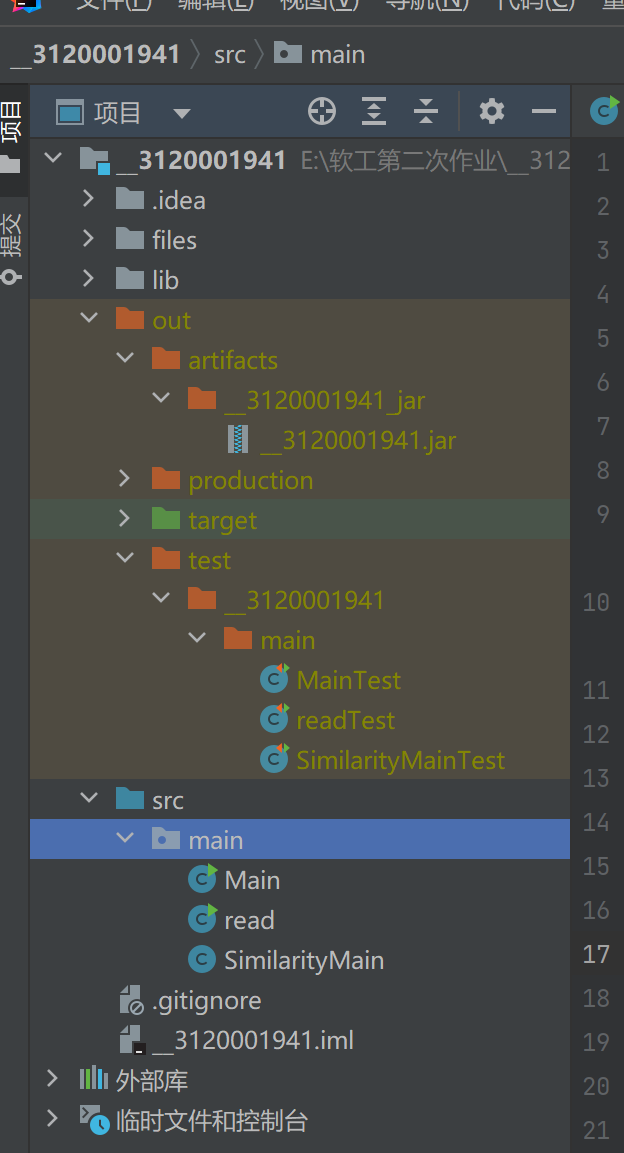
四、算法分析
余弦距离，也称为余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

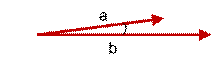
上图两个向量a,b的夹角很小可以说a向量和b向量有很高的的相似性，极端情况下，a和b向量完全重合。如下图：

上图中：可以认为a和b向量是相等的，也即a，b向量代表的文本是完全相似的，或者说是相等的。如果a和b向量夹角较大，或者反方向。如下图：

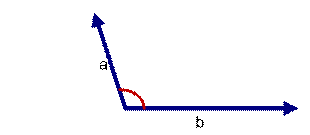
上图中: 两个向量a,b的夹角很大可以说a向量和b向量有很低的的相似性，或者说a和b向量代表的文本基本不相似。那么是否可以用两个向量的夹角大小的函数值来计算个体的相似度呢？

向量空间余弦相似度理论就是基于上述来计算个体相似度的一种方法。下面做详细的推理过程分析。

想到余弦公式，最基本计算方法就是初中的最简单的计算公式，计算夹角的余弦定值公式为：

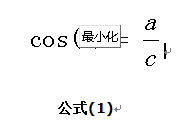
但是这个是只适用于直角三角形的,而在非直角三角形中,余弦定理的公式是：

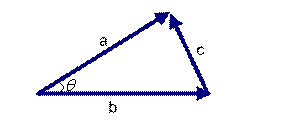
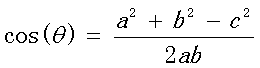
在向量表示的三角形中，假设a向量是（x1, y1），b向量是(x2, y2)，那么可以将余弦定理改写成下面的形式：

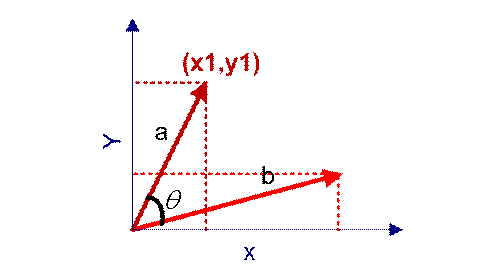
向量a和向量b的夹角 的余弦计算如下：

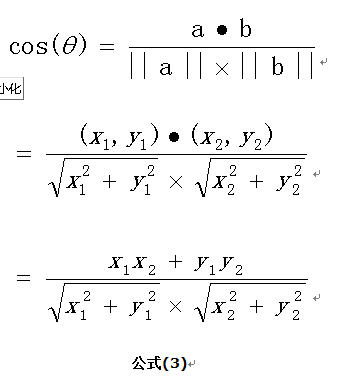
扩展，如果向量a和b不是二维而是n维，上述余弦的计算法仍然正确。假定a和b是两个n维向量，a是 ，b是 ，则a与b的夹角 的余弦等于：

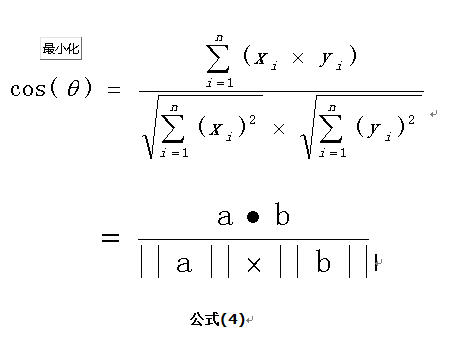
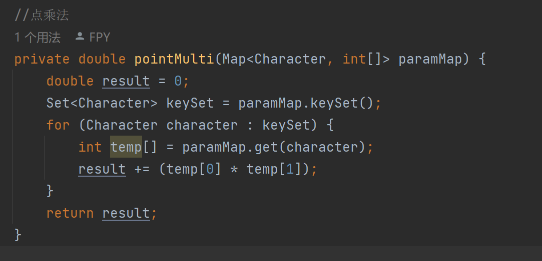
代码示例

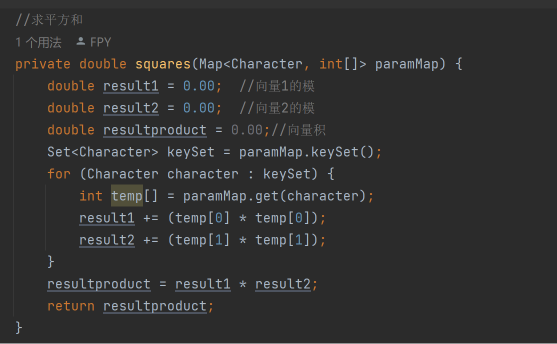
五、测试数据
对比结果：

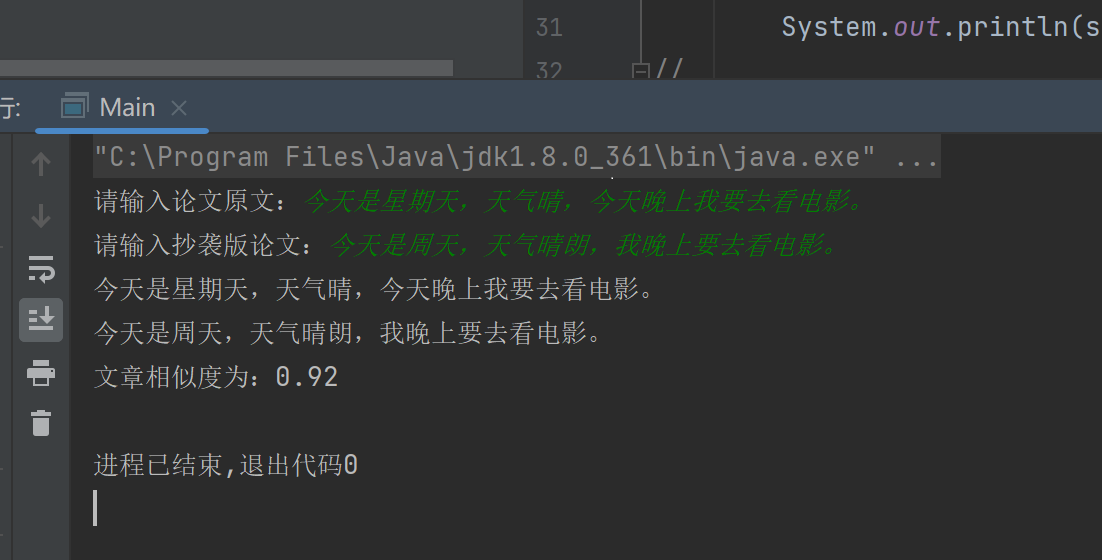
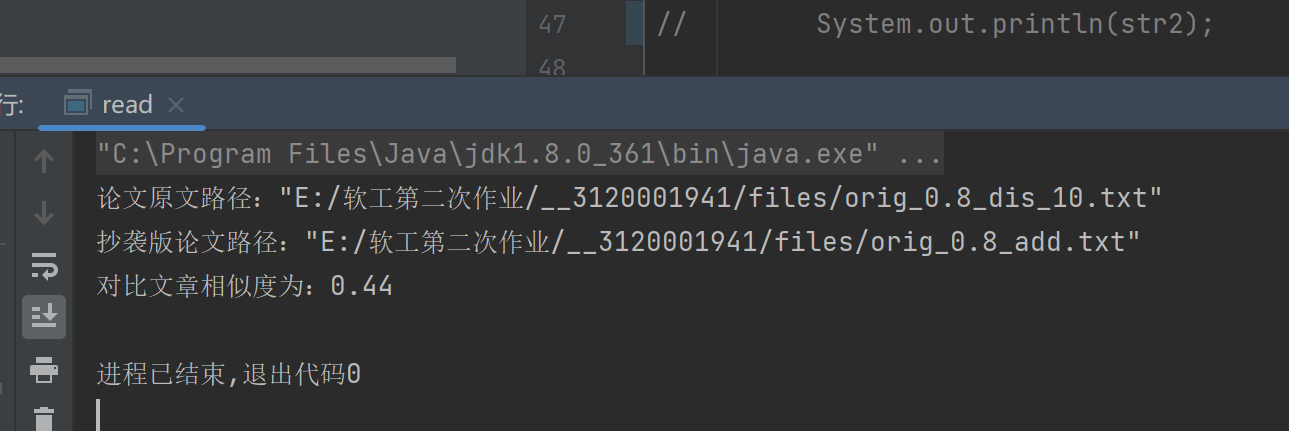
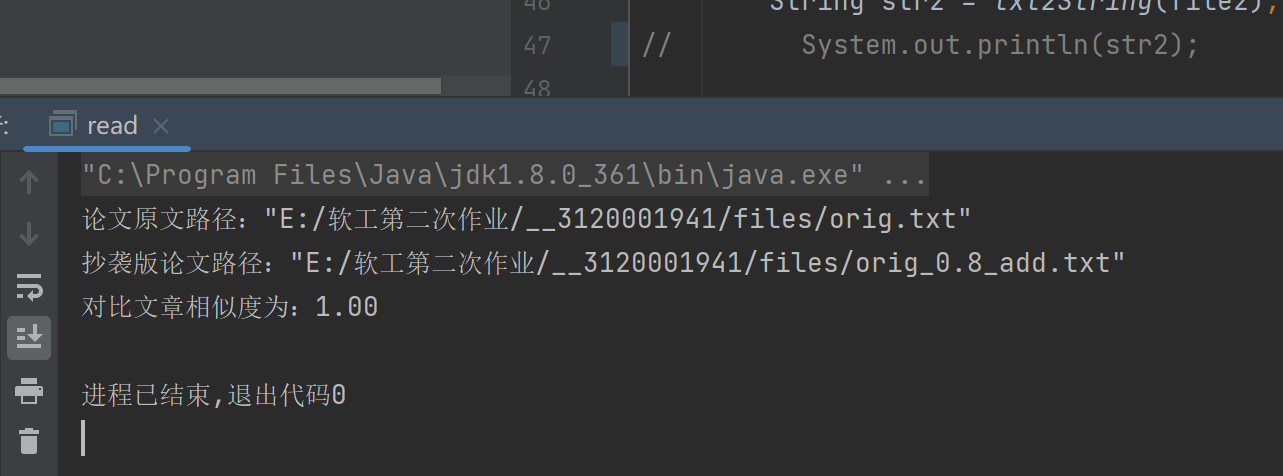
单元测试：