题解：CF1720E Misha and Paintings

题目传送门

题意

给定一个大小为 \(n\times n\) 的矩阵，每个位置上有一个数字 \(a_{i,j}\)，每次操作可以选择一个子矩阵，将子矩阵中的所有数字变为 \(0\) 到 \(n\times n\) 中的任意一个数，求满足矩阵中不同数字的种类为 \(m\) 的最少操作次数。

思路

首先先分类讨论，我们设 \(num\) 为初始矩阵中的数字种类，如果 \(num\le m\)，那么我们只需要将多次出现的相同数字每次以 \(1\times 1\) 的矩阵的形式进行修改即可，这样修改次数为 \(num-m\)。

而如果 \(num > m\)，我们手玩数据时会发现，每次的修改次数都 \(\le 2\)。现在我们考虑如何证明。

首先，令左上角 \((1,1)\) 的位置为第一个操作矩形的左上角，不断增加这个矩形的长度 \(len\)，我们定义 \(m'\) 为矩形中完全包含的数字种数，即这种数字只在这个矩形中出现，直到到达一种情况，使得 \(num-m'\le m\)，且如果 \(len+1\) 则 \(num-m'> m\)。现在我们在 \((len+1,len+1)\) 的位置放置我们的第二个矩形，为它的右下角，让它的长度不断增加，每次长度 \(+1\) 都会有两个新的数字被包含进来，\(m'\) 每次最多会增加 \(2\)。最后 \(m'\) 会等于 \(m\) 或 \(m-1\)，但是注意到我们还没有考虑这两个矩形的颜色，如果 \(m'=m\) 我们就让这两个矩形颜色相同，否则我们让这两个矩形颜色不同，这样就多增加了一个贡献，所以 \(m'\) 一定等于 \(m\)。

下面附上一张图方便理解：

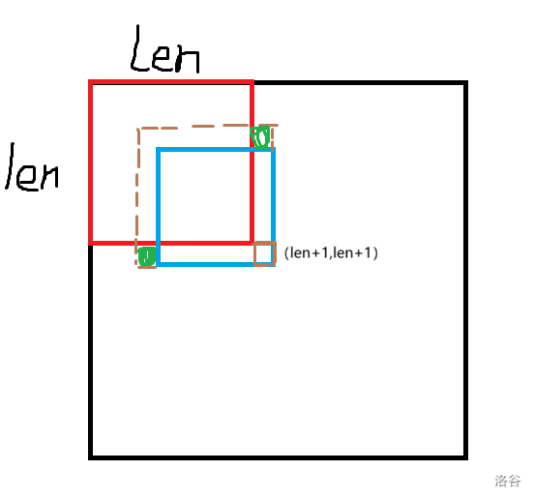
那么我们只需要确定当前矩阵能不能用一次操作解决就行了。这个比较简单。我们先预处理处包含每种颜色所需的最小矩形的左上角和右上角。我们每次统计以 \((i,j)\) 为左上角，长度为 \(len\) 的矩阵中能否包含当前颜色的最小矩形，如果可以，那么我们就用二维差分记录一下，最后再跑一遍二维前缀和即可。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1010;
const int M=1010101;
ll n,m,num;
ll a[N][N],vis[M],maxni[M],maxnj[M],minni[M],minnj[M];
ll sum[N][N];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>a[i][j];
            vis[a[i][j]]++;
        }
    }
    for(int i=1;i<=n*n;i++)minni[i]=minnj[i]=n+1;
    for(int i=1;i<=n*n;i++)if(vis[i])num++;
    if(num<=m){
        cout<<m-num;
        return 0;
    }
    for(ll i=1;i<=n;i++){
        for(ll j=1;j<=n;j++){
            ll x=a[i][j];
            maxni[x]=max(maxni[x],i);
            maxnj[x]=max(maxnj[x],j);
            minni[x]=min(minni[x],i);
            minnj[x]=min(minnj[x],j);
        }
    }
    for(int len=1;len<=n;len++){
        for(int i=1;i<=n*n;i++){
            if(!maxni[i]||!maxnj[i])continue;
            ll mxi=max(maxni[i]-len+1,1ll);
            ll mxj=max(maxnj[i]-len+1,1ll);
            ll mni=min(minni[i],n-len+1);
            ll mnj=min(minnj[i],n-len+1);
            if(mxi<=mni&&mxj<=mnj){
                sum[mxi][mxj]++;
                sum[mni+1][mxj]--;
                sum[mxi][mnj+1]--;
                sum[mni+1][mnj+1]++;
            }
        }
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(num-sum[i][j]==m||num-sum[i][j]+1==m){
                    cout<<1;
                    return 0;
                }
            }
        }
        for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)sum[i][j]=0;
    }
    cout<<2;
    return 0;
}