机器学习:P3-P4 Regression

Application

Stock Market Forecast

Self-driving Car

Recommendation

Linear model

基本形式:\(y=b+\sum w_i x_i\)

损失函数Loss function L : Input: a function, output: how bad it is

\(L(f)=L(w,b)=\sum_{n=1}^N(\widehat{y}^n-(b+w*x_{cp}^n))^2\)

$f^*=\arg minL(f) $ 在所有\(f\)中找到使得损失函数L最小的

\(w^*,b^*=\arg min L(w,b)=\arg min \sum_{n=1}^N(\widehat{y}^n-(b+w*x_{cp}^n))\) 在所有\(w,b\)中找到使得L最小的

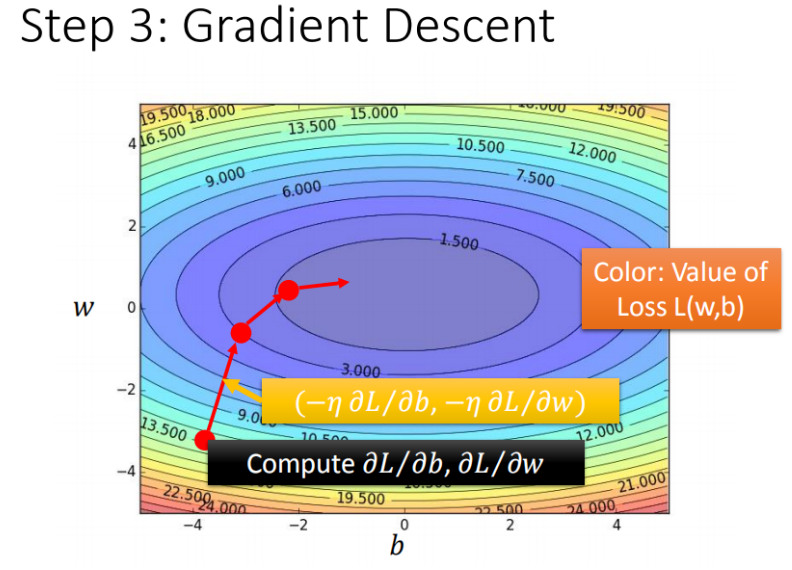
Gradient Descent

用梯度下降法求解

• consider loss function L(w) with one parameter w:

  1. (Randomly)Pick an initial value \(w^0\)

  2. Compute \(\frac{dL}{dw}|_{w=w^0}\) \(w^0-\eta\frac{dL}{dw}|_{w=w^0}\)-->\(w^1\)

  3. Compute \(\frac{dL}{dw}|_{w=w^1}\) \(w^1-\eta\frac{dL}{dw}|_{w=w^1}\)-->\(w^2\)

....many iteration

​ 一阶导数越大，走的步长越大

• How about two parameters?

  1. (Randomly)Pick an initial value \(w^0，b^0\)

  2. Compute \(\frac{\partial L}{\partial w}|_{w=w^0}\) \(w^0-\eta\frac{\partial L}{\partial w}|_{w=w^0}\)-->\(w^1\)

     Compute \(\frac{\partial L}{\partial b}|_{w=w^0}\) \(b^0-\eta\frac{\partial L}{\partial b}|_{b=b^0}\)-->\(b^1\)

  3. Compute \(\frac{\partial L}{\partial w}|_{w=w^1}\) \(w^1-\eta\frac{\partial L}{\partial w}|_{w=w^1}\)-->\(w^2\)

     Compute \(\frac{\partial L}{\partial b}|_{b=b^1}\) \(b^1-\eta\frac{\partial L}{\partial b}|_{b=b^1}\)-->\(b^2\)

  ....many iteration

  分别对每个参数求偏导
  对于线性模型，梯度下降一定能找到最优解
  

  梯度\(\nabla L=\begin{equation}\left[\begin{array}{c}\frac{\partial L}{\partial w}\\\frac{\partial L}{\partial b}\end{array}\right]\end{equation}\)

• How's the results?

  Generalization

  care about is the error on new data.

selecting another model

\(y=b+w_1*x_{cp}+w_2*(x_{cp})^2....+...+...\)

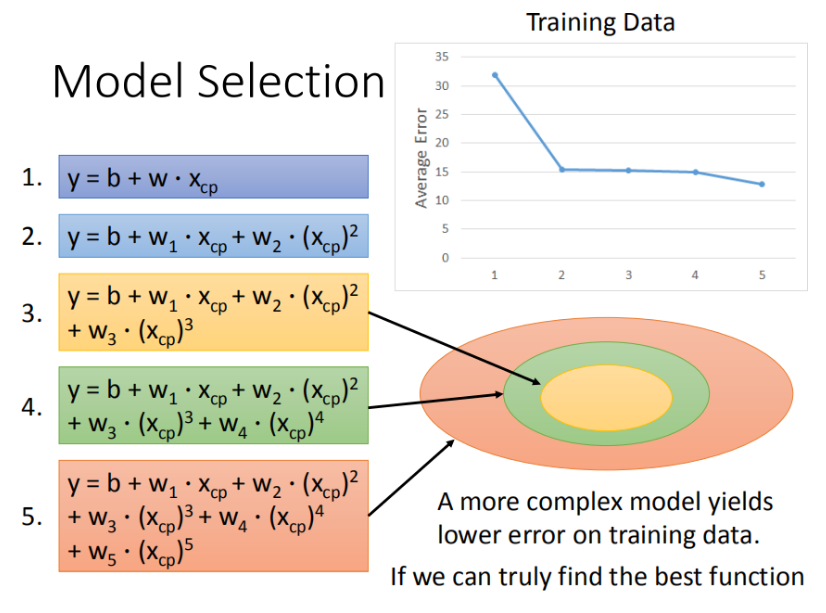
用高次函数当Model

但模型在训练数据上效果好，在testdata里面可能反而会变差

存在过拟合Overfitting现象

优化

1.根据不同种类的数据，用不同的Model去训练

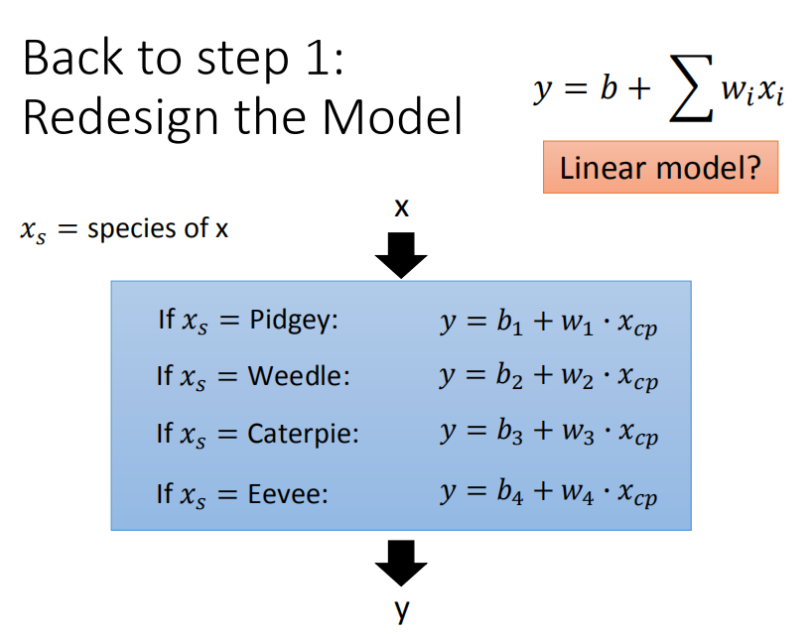
2.加入正则化Regularization选择更平滑的模型