基础绘图（有向、无向、权重、迪杰斯特拉）

在线绘图网站：

Graph Editor (csacademy.com)

1.基础绘图

1.1无权重图

graph(s,t)可以在s和t中的对应节点之间创建边并生成图
s和t必须具有相同的元素数
注意：编号从1开始，且是连续的编号

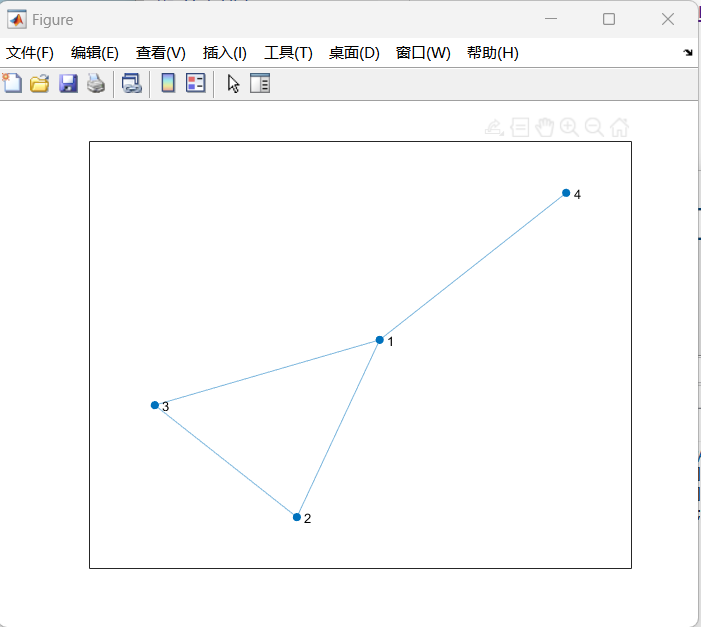
s1 = [1,2,3,4];
t1 = [2,3,1,1];
G1 = graph(s1,t1);
plot(G1)

% 通过下面这句可以不显式坐标轴
% set(gca,'XTick',[],'YTick',[]);

1.2有权重图

graph(s,t,w)
其中plot(G2,'EdgeLabel',G2.Edges.Weight)注意一定要写后面两个参数，不然不会显示权重

矩阵特点：对称矩阵，主对角线元素为0

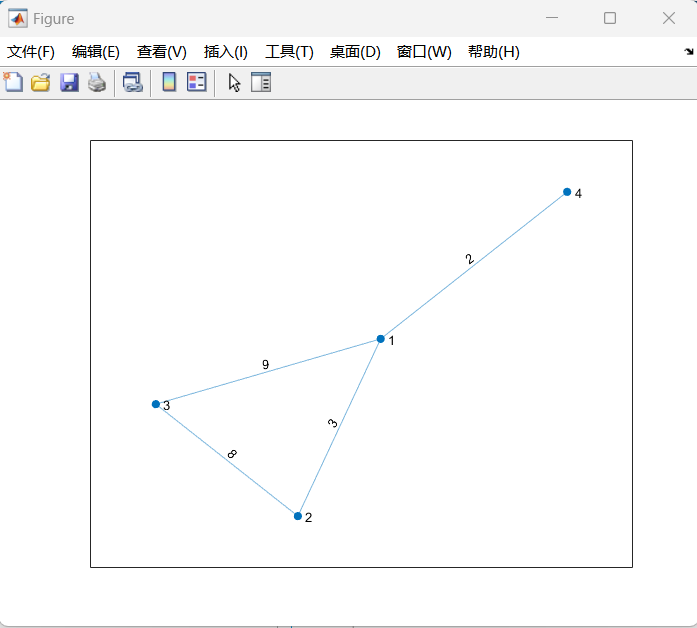
s2 = [1,2,3,4];
t2 = [2,3,1,1];
w2 = [3,8,9,2];
G2 = graph(s2,t2,w2);
plot(G2,'EdgeLabel',G2.Edges.Weight)

 1.3有向图

无权重：digraph(s,t)

有权重：digraph(s,t,w)

有权重的矩阵特点：大多数不是对称矩阵，主对角线为0，Dij指第i到j节点的权重

1.迪杰斯特拉Dijkstra算法

app推荐： 算法动画图解  

迪杰斯特拉不能处理负权重

每次都是找最短路径，然后不断延伸

初始：

 

 

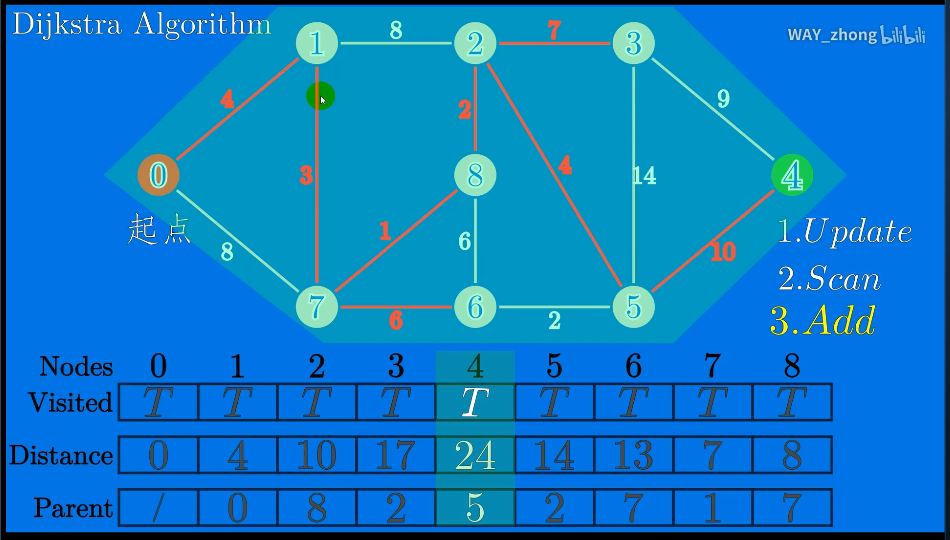
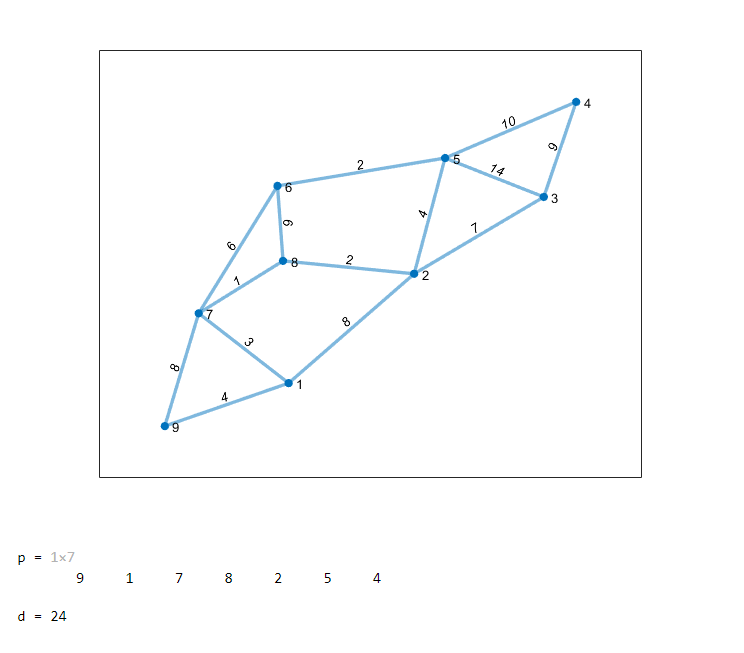
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);
plot(G,'EdgeLabel',G.Edges.Weight,'linewidth',2)
[p,d] = shortestpath(G,9,4)
% 高亮最短路径
myplot=plot(G,'EdgeLabel',G.Edges.Weight,'linewidth',2);
highlight(myplot,p,'EdgeColor',"red")

% 求任意两点的最短路径矩阵
D = distances(G)
D(1,2) %1-->2最短路径
D(9,4) %9-->4最短路径

% 查找给定的节点内所有的点
%[nodeIDs,dist] = nearest(G,s,d,['方法']) s:节点，d距离
%nodeIDs返回序号，dist返回距离
[nodeIDs,dist] = nearest(G,2,10)

 

 

 

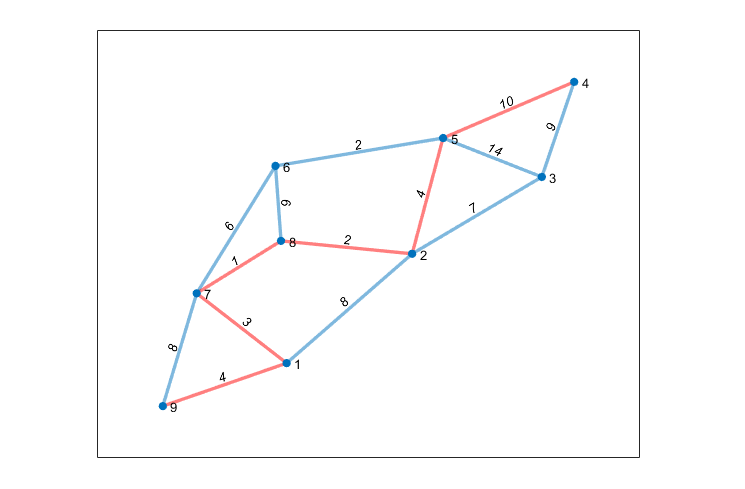
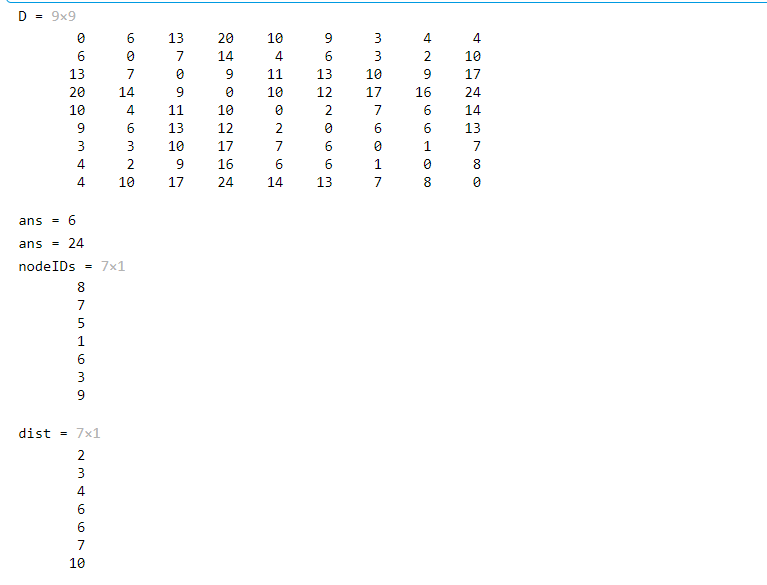
//2.贝尔曼-福特Bellman-Ford算法